要在橋牌紙牌遊戲中獲勝(由兩組搭檔進行),一名玩家必須以某種方式向隊友示意他們手牌的強度。 心靈感應在這裡會派上用場。 但是心靈感應不是真的,對吧?
這是正確的。 然而,幾十年來,物理學家一直懷疑,如果橋牌是用受量子力學規則約束的紙牌進行,那麼看起來非常像心靈感應的事情應該是可能的。 現在,中國的研究人員已經透過實驗證明了這種所謂的量子偽心靈感應——不是在量子橋牌中,而是在一個名為 Mermin-Peres 魔方 (MPMS) 遊戲的雙人量子競賽中,其中獲勝要求玩家在不相互交換資訊的情況下協調他們的行動。 如果運用得當,量子偽心靈感應可以讓玩家贏得遊戲的每一輪——這是原本不可能實現的完美表現。 這項使用雷射光子進行的實驗,探測了量子力學在允許粒子之間共享資訊方面的極限。
印度馬德拉斯理工學院的 Arul Lakshminarayan 說,這項工作“是對 Mermin-Peres 魔方遊戲的一個美麗而簡單的直接實現”,他沒有參與實驗演示。 他補充說,它的美部分來自於它優雅地證實了量子系統的狀態在實際測量之前沒有明確定義——這通常被認為是量子力學最令人困惑的特徵。 “這些量子游戲嚴重破壞了我們關於物體具有透過觀察揭示的預先存在屬性的共同概念,”他說。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。 透過購買訂閱,您正在幫助確保未來能夠繼續報道關於塑造我們今天世界的發現和想法的具有影響力的故事。
兩位量子物理學家 Asher Peres 和 David Mermin 在 1990 年獨立設計了 MPMS。 它涉及兩名玩家(按照量子力學思想實驗的傳統,稱為 Alice 和 Bob),他們必須填寫一個“魔方”——一個三乘三的數字網格——每個網格元素都被分配一個 +1 或 -1 的值。 在每一輪中,裁判(Charlie)隨機發送一行給 Alice,隨後傳送一列給 Bob(總共有九種這樣的行和列組合)。 玩家必須告訴 Charlie 在他們的三個網格空格中放入哪些 +1 或 -1 的值。 與任何魔方挑戰(例如數獨)一樣,每行和每列的總和必須滿足特定的約束:這裡,一行中所有條目的乘積必須等於 +1,而所有列的乘積必須為 -1。 如果 Alice 和 Bob 都為列和行重疊的網格元素分配相同的值,則他們贏得一輪。
經典上,不可能贏得所有輪次,因為即使 Alice 和 Bob 每次都猜得很好,但對於每個完成的方格,都不可避免地有一輪他們的分配必須衝突。 他們能做的最好的就是每九輪贏得八輪。
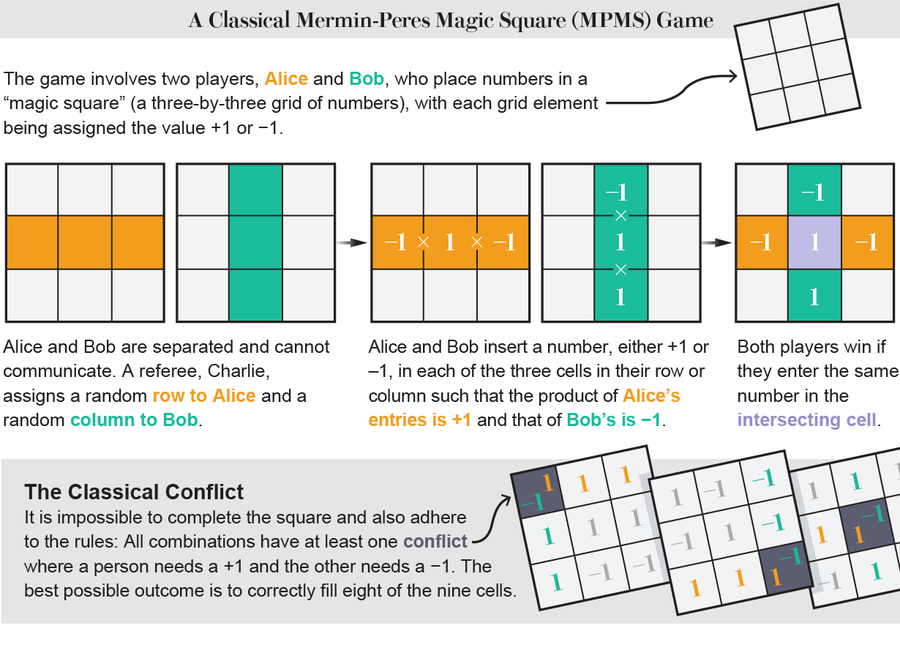
圖片來源:Lucy Reading-Ikkanda
但是現在假設 Alice 和 Bob 可以使用這種量子策略:他們不是為每個網格元素分配 +1 或 -1 的值,而是為其分配一對量子位元(qubit),每個量子位元在測量時都有 +1 或 -1 的值。 每個玩家給特定網格元素的值是透過測量兩個量子位元值並找到這對量子位元的乘積來確定的。 現在可以避免經典的衝突,因為 Alice 和 Bob 可以根據他們進行測量的方式從相同的兩個量子位元中獲得不同的值。 有一種特定的測量策略可以確保任何給定輪次的獲勝標準——Alice 和 Bob 的三個條目的乘積分別為 +1 和 -1——在行和列的所有九種排列中都得到滿足。
然而,這種策略存在一個問題。 為了進行正確的一組測量,Alice 和 Bob 需要知道他們的三個網格元素中哪一個是與另一位玩家的網格元素重疊的——他們需要協調。 但在 MPMS 中,這不是問題,因為他們對相同的三個量子位元對進行順序測量。 這意味著到達 Bob 的量子位元對具有 Alice 已經如何測量這些量子位元的印記:他們可以相互傳遞資訊。
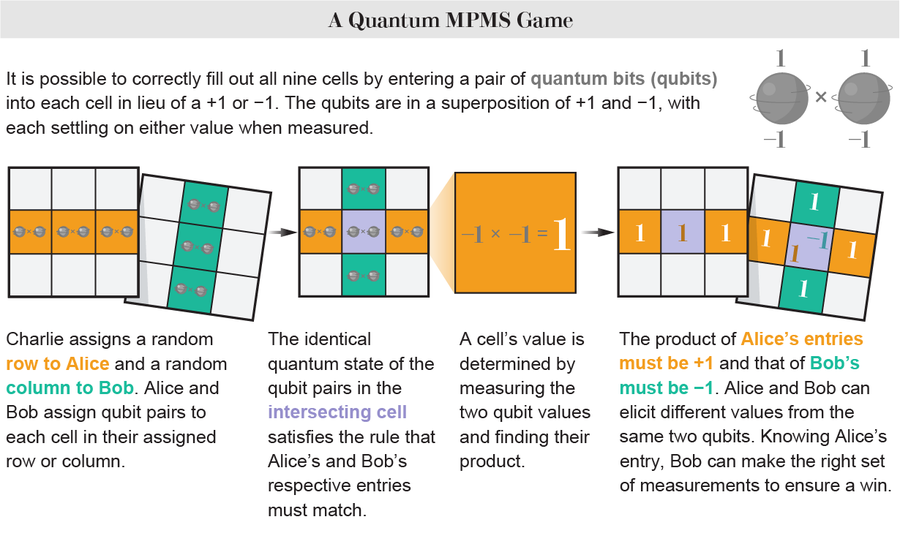
圖片來源:Lucy Reading-Ikkanda
1993 年,Mermin 表明 MPMS 可用於演示一種稱為上下文性的量子現象。 上下文性最初由北愛爾蘭物理學家 John Stewart Bell 於 1966 年提出,指的是量子測量的結果可能取決於測量方式。 系統中的一組經典測量將給出相同的結果,無論這些測量以什麼順序執行。 但對於量子測量,情況並非總是如此。 在 MPMS 中,上下文性源於這樣一個事實:給定量子位元對的測量結果可能因同時測量的其他兩個量子位元對而異。
但是,如果我們禁止 MPMS 中的任何通訊,方法是為 Alice 和 Bob 分配不同的量子位元對,並說他們不能商量如何測量它們,那會怎麼樣? 那麼,只有當每個玩家對另一位玩家所做的事情做出正確的猜測時,他們才能保證九輪全勝。 但在 2005 年發表的一項研究中,蒙特利爾大學的量子理論家 Gilles Brassard 及其同事表明,即使不進行通訊,玩家也可以使用他們所謂的量子偽心靈感應,利用量子原理來保證每輪都獲勝。
這種策略涉及將傳送給 Alice 或 Bob 的每對量子位元中的一個量子位元與另一位玩家使用的相應量子位元糾纏在一起。 糾纏粒子具有相關的屬性,因此如果 Alice 測量了她的粒子的值,那麼 Bob 的粒子的值也會被固定下來。 兩個糾纏的量子位元粒子可能是反相關的,這樣如果發現 Alice 的量子位元的值為 +1,則 Bob 的量子位元的值必須為 -1。 在測量之前,無法知道 Alice 的量子位元具有哪個值——它可能是 +1 或 -1。 但 Bob 的量子位元將始終與其相反。 更重要的是,粒子對之間糾纏的屬性被稱為“非局域性”,這意味著它不是“局域”於任何一個粒子,而是在兩者之間共享。 即使粒子相隔遙遠,糾纏對也必須被視為一個單一的、非局域的物件。 2001 年,西班牙塞維利亞大學的量子理論家 Adán Cabello 在他稱之為“all or nothing”的遊戲中提出了贏得量子游戲的相同基本思想,後來證明該遊戲等同於非局域(偽心靈感應)MPMS。
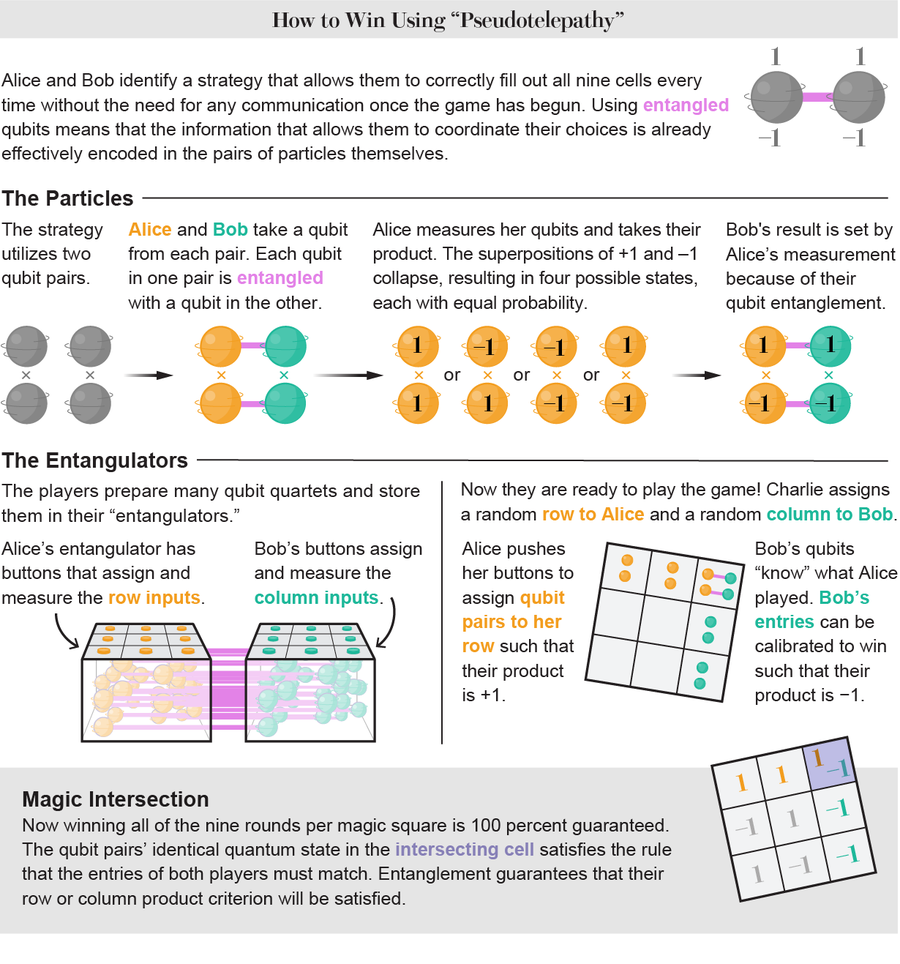
圖片來源:Lucy Reading-Ikkanda
一些研究人員認為糾纏是量子力學最基本的方面。 它暗示了粒子之間的一種資訊共享。 這是利用糾纏進行量子偽心靈感應的關鍵:Alice 和 Bob 不必交換資訊來協調他們的行動,因為必要的資訊已經共享在粒子對本身中。
上下文性和非局域性都提供了“量子資源”,可用於獲得相對於經典資訊處理方法的一些優勢。 例如,在量子計算中,量子位元之間的糾纏通常是建立經典計算機無法獲得的解決問題的捷徑的資源。
物理學家已經使用糾纏光子在現實世界中反覆演示了 Cabello 的全有或全無遊戲。 但是,雖然這些實驗確立了糾纏如何透過擊敗經典效能來傳達“量子優勢”,但中國科學技術大學的陳凱、中國南京大學的王錫林及其同事設計了一項新的實驗,他們說該實驗實現了完整的協議,以實現每輪都保證獲勝——真正的、一致的量子偽心靈感應。
理想情況下,Alice 和 Bob 會在遊戲開始前準備多組四個量子位元,每組四量子位元包含兩對糾纏對。 Alice 會得到每對量子位元中的一個,Bob 會收到另一個。 然而,研究人員表示,為遊戲的每一輪製作兩對糾纏光子極具挑戰性。 首先,在他們的裝置中,即使產生一對糾纏對的機率也很低,因此一次製作兩對的可能性極低。 而且,正如偽心靈感應 MPMS 所要求的那樣,對於這種光學實現來說,同時檢測兩對量子位元對幾乎是不可能的。
相反,陳、王及其同事製備了單光子對,並獨立地糾纏了它們的兩個屬性:它們的偏振態和稱為軌道角動量的屬性。 光子包含在持續時間僅為 150 飛秒的超短雷射脈衝中,並透過穿過兩個所謂的非線性光學晶體而發生糾纏。 一塊薄薄的硼酸鋇板首先將一個單光子分裂成兩個能量較低且具有相關角動量的光子。 然後,它們也透過偏振進行糾纏,方法是將其傳送透過釔釩化合物的晶體。
為了證明接近 100% 的成功率,研究人員需要提高他們的檢測效率,以便幾乎沒有糾纏光子在未被發現的情況下逃脫。 即使這樣,在實驗中也無法精確達到理論極限——但研究人員能夠證明,他們可以以 91.5% 到 97% 的機率贏得每一輪。 這個範圍轉化為在總共進行的 1,075,930 輪比賽中,可靠地擊敗了經典八勝一負的限制,共計 1,009,610 輪。
陳說,偽心靈感應 MPMS 遊戲利用了量子力學可能提供的粒子之間最強的相關程度。 “我們的實驗探索瞭如何在粒子之間產生極端的量子相關性,”他說。 如果這些相關性再強一些,它們將暗示超光速資訊交換,而許多其他獨立實驗表明這是不可能的。
Mermin 說,雖然實驗結果令人印象深刻,但這種成功並沒有揭示任何超出量子力學按我們想象的那樣運作的事實。 Cabello 並不完全同意。 他說,除了是一場實驗性的技術壯舉之外,這項工作還展示了量子規則透過同時調動兩個量子優勢來源而使之成為可能的新變化:一個與非局域性相關,另一個與上下文性相關。 Cabello 說,同時研究這兩種效應應該讓物理學家能夠更嚴格地探索它們之間的聯絡。
更重要的是,原則上,這些資源中的每一個都可以用於量子處理中的不同用途,從而提高其多功能性。 “例如,非局域性可以用於秘密通訊[使用量子密碼術],而上下文性可以用於量子計算,”Cabello 說。 在這種情況下,例如,Bob 可以與 Alice 建立安全通訊,同時與 Charlie 進行比經典方法允許的更快的計算。
Lakshminarayan 說,在這些實驗中使用共享糾纏“導致了在經典上看起來很神奇的效果”。 但是,鑑於量子力學經常被誤用作為偽科學主張的虛假理由,將這種現象稱為“偽心靈感應”是否會自找麻煩? Mermin 說,這是一個“邀請荒謬解釋的糟糕術語”。 但雖然 Cabello 同意,但他承認,引人入勝的名字可以幫助宣傳這種現象的趣味性。 “我們不要自欺欺人,”他說。 “可能正是由於‘偽心靈感應’這個詞,[你和我]才正在進行這次對話。”
