想象一下,您正在為六位客人舉辦一個小聚會,但不清楚誰認識誰,誰不認識誰。 事實證明,必然至少有三個人彼此完全陌生,或者至少有三個人已經是朋友。(我們並非假設您的朋友不喜歡彼此。)因此,總是會至少有一組三個人,他們彼此都認識或完全不認識。
乍一看,這聽起來可能並不太令人驚訝,但您越思考這個問題,它就越有趣。 六個人彼此之間有 15 個聯絡。 因此,您可能會問,A 如何與 B 相關? A 如何與 C 相關? B 認識 C 嗎? 這些聯絡可以有兩個值之一:朋友或陌生人。 這意味著,僅有六位客人,就已經有 215 (32,768) 種不同的方式讓聚會參與者彼此聯絡。 而數學主張,在每一種可能的分組中,總是有一個三人組,其中所有人都彼此認識,或者都是完全的陌生人。 逐個案例地查詢三人組似乎相當麻煩。
事實上,弄清楚這一點屬於拉姆齊理論的範疇,該理論以英國數學家弗蘭克·拉姆齊(Frank Ramsey,1903-1930)的名字命名,他於 26 歲時不幸英年早逝。 然而,在他短暫的一生中,他成功地發展了一個數學分支,該分支處理識別混亂中的某種秩序。 其目的是在令人困惑的排列中識別重複出現的模式,就像我們聚會參與者的情況一樣。 可以從數學的角度提出問題:您必須邀請多少位客人,才能至少有一組三個人彼此都認識,或者至少有一組三個人完全陌生?
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。
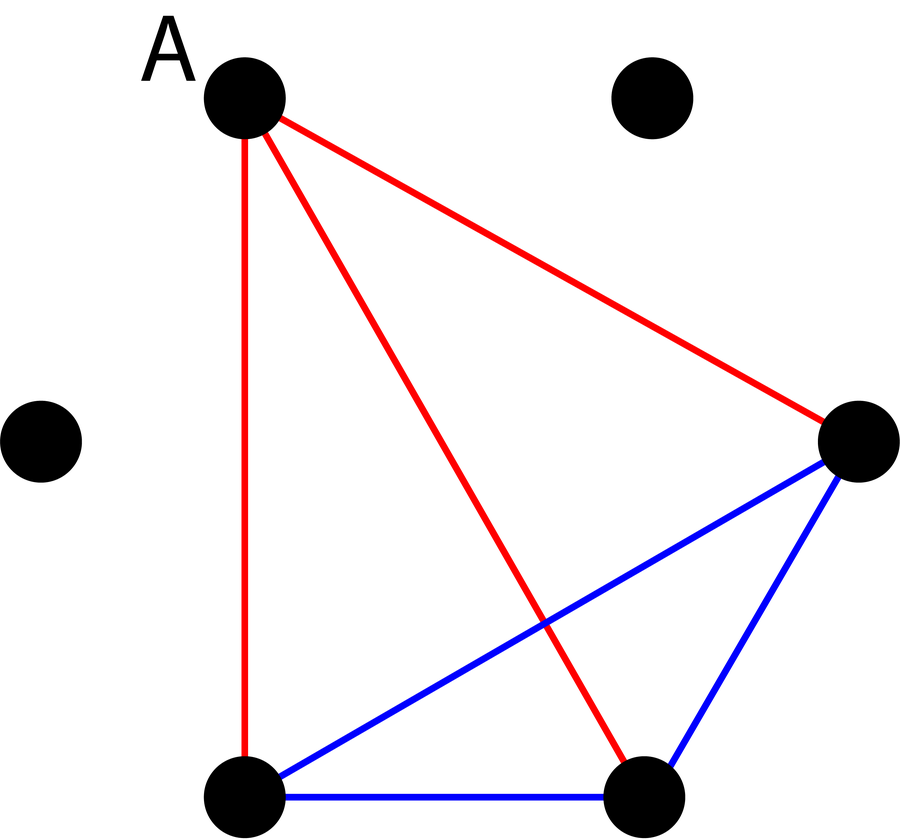
整個事情可以用圖形或圖表來解決,這些圖形或圖表是點(也稱為節點)和邊(連線點的線)的網路。 每個人都象徵著一個節點。 六位客人可以圍成一個圓圈排列。 現在每個點都已連線。 這就產生了 15 條邊。 根據兩個人是否彼此認識,它們被塗成紅色(表示熟人)或藍色(表示陌生人)。 現在宣告:無論您如何為邊著色,您總是會得到一個單色三角形——一個全藍色或全紅色的圖形。
現在拉姆齊理論提出的附加宣告:對於剛才提到的六位客人,無論您如何為邊著色,您總是會得到至少一個單色三角形——一個全藍色或全紅色的圖形。 如果您嘗試一下,您會看到這樣的三角形總是會出現。
當然,沒有人願意瀏覽 32,768 種可能性。 這樣做也不會回答拉姆齊提出的一個問題,即六是否是不可避免地形成這樣一個三角形的最小客人人數。 您可以嘗試透過更改邀請人數來解決這個問題。 如果您找到以某種方式著色的三角形,使得根本沒有出現單色三角形,那麼您就找到了相反的證據。 如果您只邀請三位客人,其中兩個人可能之前見過面。 因此,在這種情況下,沒有三個人是彼此都認識或彼此陌生的——因此沒有單色三角形。
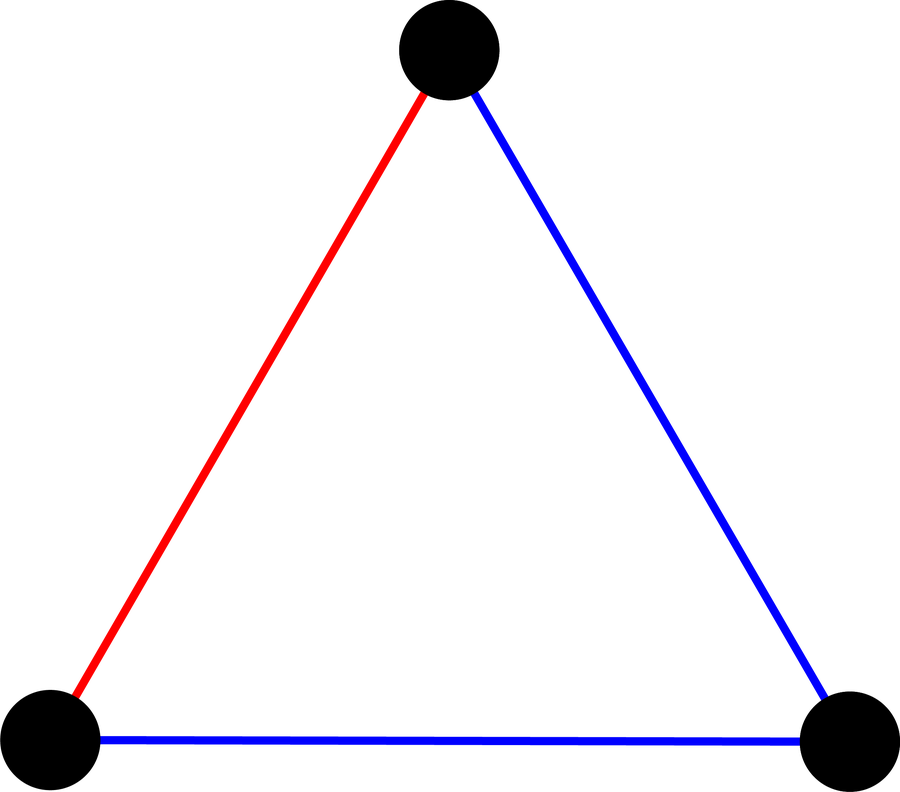
對於四個人來說,也很容易找到沒有一組三個人彼此不認識或彼此是朋友的情況。
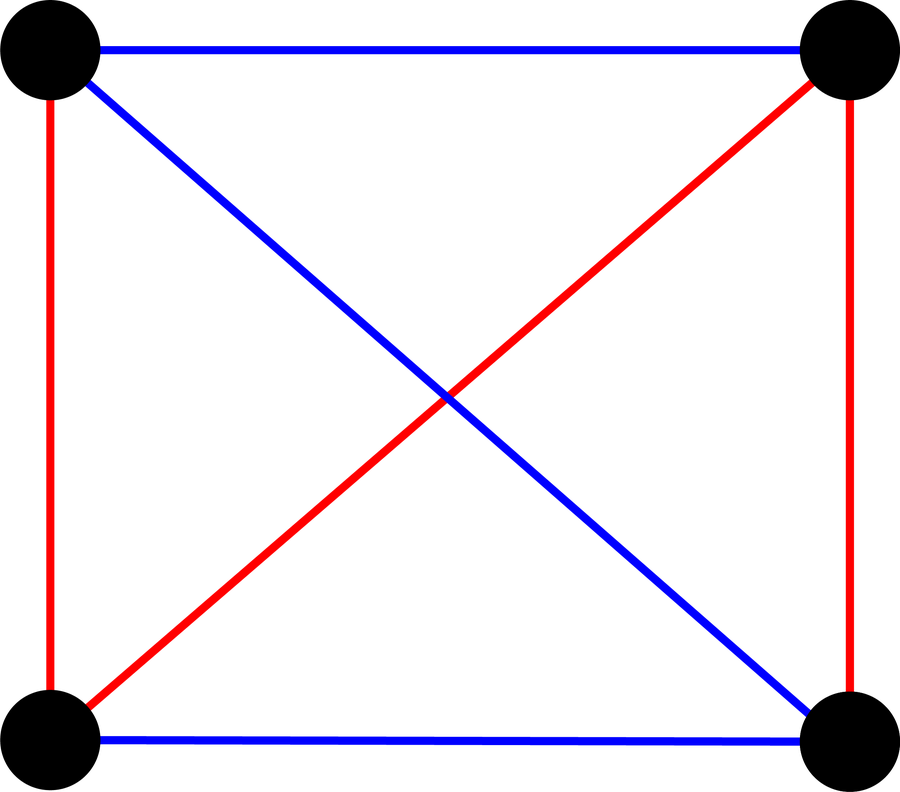
即使有五位客人,也至少有一種朋友-陌生人連線的配置,而沒有相同顏色的三角形。 因此,要回答拉姆齊關於最小的聚會參與者群體的問題,他們的關係總是可以用至少一個單色三角形來描繪,這個數字必須大於五。 但要大多少呢?
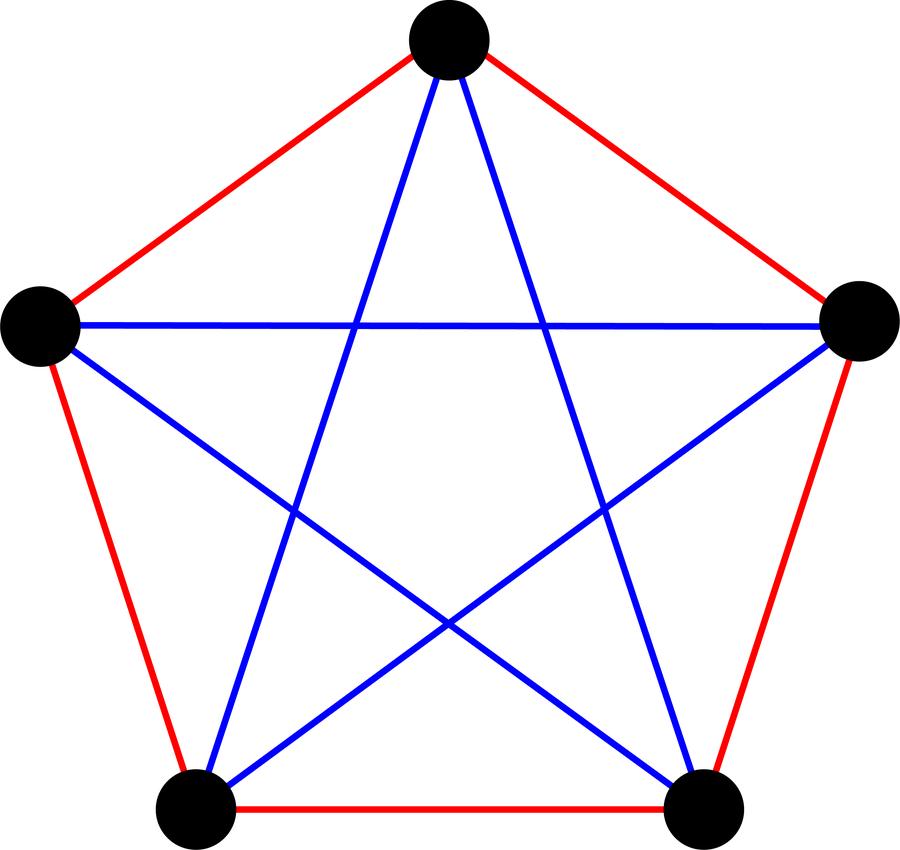
當我們達到六個人時會發生什麼? 您現在必須嘗試為圖表的邊著色,而不建立單色三角形。為此,您可以首先挑選出一個人 A,並檢查他們與其餘客人的關係可能是什麼。 假設 A 是聚會的女主人。 在受邀者中,她有多少朋友? 有六種不同的方式將她與五位客人聯絡起來:例如,她可能沒有朋友,在這種情況下,五位受邀者都對她來說是陌生人。 或者她可能有一位朋友,在這種情況下,有四位陌生人。 此圖表顯示了六位聚會參與者可能與女主人聯絡的各種方式。
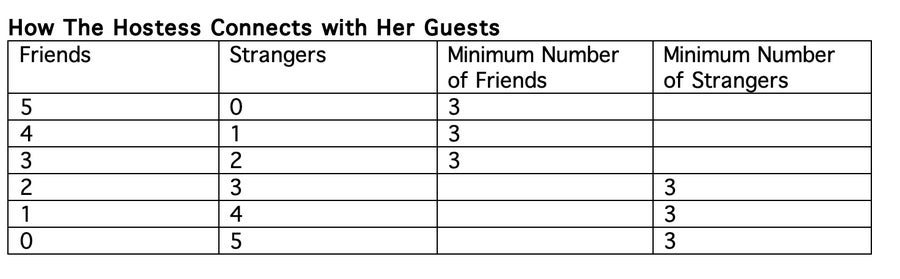
女主人(A)至少與三個人是朋友——或者至少有三個人對她來說是陌生的。 在圖表中,可以透過她總是至少有三條相同顏色的邊來看出這一點。 使用一個具體的例子,可以假設,在表中顯示的配置之一中,女主人有三條紅色邊,這意味著她認識其他三位客人。 現在您可以嘗試為剩餘的連線著色,以避免在 32,768 種可能的著色組合中出現紅色三角形。

因此,您必須確保任何兩個認識女主人的客人彼此不認識——他們之間必須有藍色連線。 但是,如果您將所有這些邊都標記為藍色,您將得到一個藍色三角形! 也就是說,如果所有節點都必須連線,則無法避免六點圖中的單色三角形。 而且您可以在所有點都連線的任何更大的圖中找到這樣的三角形。 這意味著,只要您邀請超過五位客人,就總會有一組三個人彼此都認識或彼此都不認識。
當然,數學家不會滿足於單一的結果。 相反,他們試圖概括問題。 因此,為了推匯出拉姆齊數的一般情況,他們會問:“R 需要多少個最少節點才能總是找到紅色 m-團或藍色 n-團。 n-團表示一組彼此全部連線的 n 個點。 結果數 R(m,n) 稱為拉姆齊數。 令人驚訝的是,已知的拉姆齊數非常少。 我們剛剛證明了 R(3,3) = 6。 也可以證明 R(4,4) = 18。 這意味著,如果您邀請 18 位客人參加聚會,則總會有一組四個人彼此都認識或彼此都不認識。
然而,幾十年來,R(5,5) 有多大一直不清楚。 換句話說,您必須邀請多少位客人才能總是有一個五人組,他們要麼都是熟人,要麼都是陌生人? 專家們已經能夠縮小結果範圍:我們現在知道 R(5,5) 落在小於或等於 43 個節點的下限和小於或等於 48個節點的上限的範圍內。似乎我們可以簡單地使用計算機來遍歷具有 43 個節點的圖的所有可能的著色,看看是否存在一個不包含五個相同顏色組的圖。 但事實上,這項任務超出了任何可用的計算能力!
一個具有 43 個節點且全部連線的圖有 903 條邊。 這些邊可以是紅色(朋友)或藍色(陌生人)。 這就是 2903 種可能性,四捨五入約為 10272 。 這是一個 1 後面跟著 272 個零,這是難以想象的巨大數字。 為了理解它有多大,可以這樣想:目前假設我們的宇宙由大約 1082 個原子組成。
假設每個原子都是一臺計算機器,它每秒可以執行與目前最強大的超級計算機一樣多的計算次數:每秒一百萬兆(1018)步計算。 假設每個原子每秒可以搜尋一百萬兆個圖,以查詢五個一組的圖——並且粒子會在 138 億年前的大爆炸之後立即開始這樣做。 那麼到目前為止,他們將有 13.8 x 109 x 365.25 x 24 x 3,600 ≈ 4.35 x 1017 秒的時間來完成這項任務。 也就是說,宇宙中的所有原子到目前為止已經檢查了大約 4.35 x 10117 個圖——僅佔剩餘要處理的一小部分。
因此,數學家們正在尋找更聰明的解決方案來解決這個問題。 然而,到目前為止,他們還沒有找到任何解決方案。
本文最初發表於 Spektrum der Wissenschaft ,經許可轉載。
