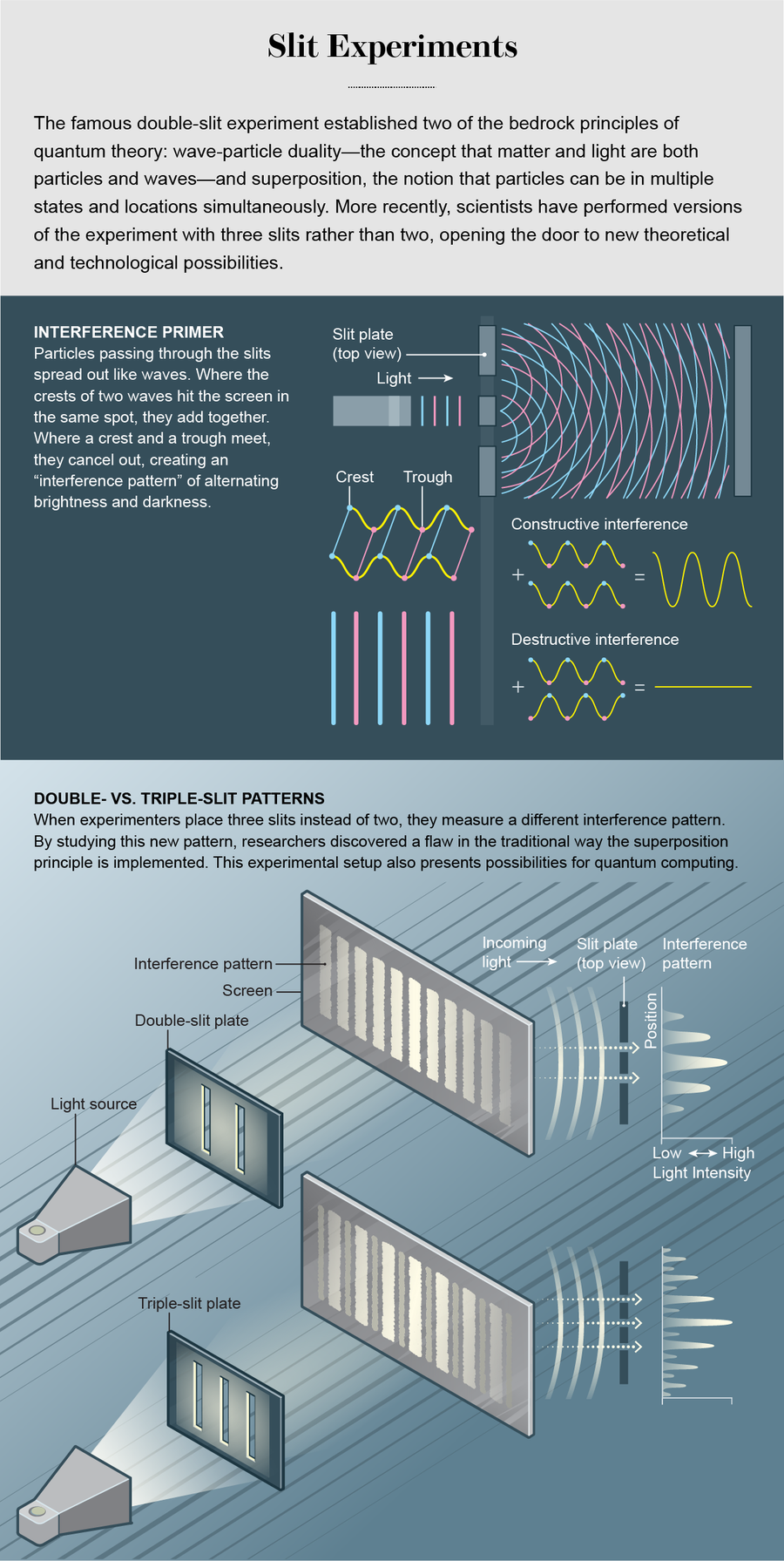
“量子力學的所有奧秘”都包含在雙縫實驗中,諾貝爾獎得主理查德·費曼曾說過一句名言。在1801年由英國博學家托馬斯·楊首次提出的實驗中,一束光子——光粒子——飛向一面牆,牆上切有兩個狹縫。當光到達牆後的螢幕時,它會產生明顯的“干涉圖案”:明暗相間的條紋。只有當光子表現得像波而不是像點粒子時,才會出現這種圖案,並且透過兩個狹縫的波的波峰和波谷相互干涉,有時會增加光,有時會抵消光。當楊使用改進的裝置進行實驗時,這似乎確立了光是一種波而不是粒子。
真的是這樣嗎?奇怪的是,在幾個世紀後的實驗中,研究人員小心地一次只向牆壁照射一個光子,干涉圖案仍然存在,就像單個粒子在與自身干涉一樣。更奇怪的是,如果你在狹縫旁放置一個探測器來記錄每個粒子透過哪個狹縫,干涉圖案就會消失。取而代之的是,你在螢幕上得到兩條光線,這正是你期望的點粒子而不是波透過時會得到的結果——就好像測量行為改變了粒子的性質一樣。
時至今日,雙縫實驗以其概念的內在簡潔性,仍然是進行過的最有趣的實驗之一。它已經被重複了很多次,使用光和物質的粒子。它清楚地展示了量子力學的基本奇異性:光和物質實際上既是粒子又是波——這個概念被稱為波粒二象性。它還確立了疊加原理:粒子可以存在於多種狀態,甚至同時存在於多個位置。在雙縫實驗中,粒子一定不能只通過一個狹縫或另一個狹縫——為了發生干涉,每個粒子都必須透過兩個狹縫。
支援科學新聞事業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的有影響力的故事的未來。
儘管這個實驗廣受讚譽,但我們尚未探究其深度。最近,我在印度班加羅爾拉曼研究所量子資訊與計算實驗室的團隊,已經在微波波長範圍內設定了“三縫”實驗——我們使用三個狹縫而不是兩個狹縫。這似乎是一個簡單的調整,但它具有深遠的意義。在理論方面,我們的三縫試驗已經闡明瞭疊加原理在這種情況下如何應用,並揭示了我們對這種現象的基本理解中的新細微之處。
我們的三縫實驗架構還在新興的量子計算領域提供了有趣的機會。量子計算機有望實現以前難以處理的計算——如果我們能夠利用量子物理學的力量來構建它們。量子計算的核心挑戰之一是找到一種方法來增加量子計算機包含的位元數(稱為量子位元),而不會破壞允許量子位元同時處於兩種狀態的疊加態——這是實現計算速度巨大提升的關鍵。當社群中的大多數人都在致力於增加系統中量子位元的數量時,我的實驗室正在嘗試一種替代的、較少探索的方法,即使用更高維度的“量子數字”而不是二維量子位元。使用三縫系統,我們可以建立稱為三元量子位元的三維量子數字。
圖片來源:尼克·博克爾曼
疊加原理
量子理論不僅將基本粒子描述為物理波,而且還描述為由所謂的波動方程決定的,其解可以用希臘字母psi,Ψ表示。這些解表示粒子處於任何特定狀態的機率幅度。
然而,我們的研究揭示了物理學家在將波動方程計算應用於雙縫實驗時,傳統處理方式中的一個缺陷。想象一下經典的實驗,讓兩個狹縫分別命名為A和B。描述該系統中粒子的波動方程的解,當狹縫A開啟時可以標記為ΨA,當狹縫B開啟時可以標記為ΨB。當兩個狹縫都開啟時會發生什麼?教科書中的常見做法是將解稱為ΨA + ΨB,以表示粒子處於疊加態,其中它同時透過兩個狹縫。這確實是疊加原理的應用,儘管是不完整的。原因很簡單:兩個狹縫同時開啟的情況與分別開啟狹縫的組合不同。我們知道,當它們同時開啟時,粒子在某種程度上會同時透過兩個狹縫並與自身相互作用,而我們不能簡單地透過將兩個解相加來表示這些相互作用。
科學家們之前已經提出,可能需要一些修正項來使我們的方程準確。這個量被稱為索爾金引數,因為它是由當時在雪城大學的物理學家拉斐爾·索爾金在1994年預測的。然而,大多數研究人員都認為這個項會非常小,以至於可以忽略不計。事實上,我們知道它不能太大,否則早就應該被觀察到了。但是我們的三縫實驗證明,這個項確實存在,並且並非總是小到可以忽略不計。使用三個或更多狹縫為我們提供了這個修正項的天然試驗平臺,因為我們可以測量一個量(索爾金引數),如果修正項不存在,則該量將為零,如果它存在,則該量將為非零。(在雙縫情況下,修正項被新增到已經非零的量中,因此它不會以明顯的方式顯示出來。)
我已經從事三縫實驗研究十多年了。2010年,我和我的同事在《科學》雜誌上發表了我們的第一個結果。2014年,我和我的團隊開始在印度卡納塔克邦的Gauribidanur天文臺使用微波進行新的三縫實驗試驗。我們在玉米地旁邊的帳篷裡的露天場地進行了這個專案。儘管對於精密物理實驗來說,這個環境聽起來可能很奇怪,但玉米為可能干擾我們測量的雜散微波提供了良好的吸收源。我們沒有在空間中使用牆壁或大量可能反射波的裝置也很有幫助。此外,我們偏遠的位置手機訊號很差——這是避免汙染的另一個好處——而且我們能夠大規模地進行實驗。
我們的裝置使用了兩個喇叭天線——一個用於釋放微波光子,另一個用於探測它們。它們之間是一個帶有三個槽的板,每個槽寬10釐米,間距13釐米。為了忠實於第一個基於狹縫的實驗風格,我們將探測器安裝在導軌上,我們可以移動導軌以測量作為探測器位置函式的不同干涉圖案。我們發現,我們測量的干涉圖案與波動方程給出的近似解ΨA + ΨB不符,但它與包含非零索爾金引數的解相符。我們還使用了阻擋材料來阻擋狹縫之間的空間,基本上阻止了光子在狹縫之間傳播並與相鄰狹縫相互作用。當我們這樣做時,我們看到索爾金引數的值隨著阻擋塊的大小而變化——這表明該引數確實測量了狹縫之間的相互作用,並且它根據相互作用的程度而變化。這一發現確立了我們測量的修正項不是我們未能理解的實驗中的某些系統誤差,而確實是我們正在尋找的東西。
我們的研究首次明確驗證了索爾金引數作為經典微波域中疊加原理的修正項。這項結果於2018年6月發表在《新物理學雜誌》上,已經導致了一些教科書的修訂,並且影響了我們對基礎物理學的基本理解。它們也可能對天文學和天體物理學中研究來自早期宇宙訊號的工作產生影響。這項研究通常涉及散佈在地面的無線電天線陣列。通常,不同天線接收到的資料會被加在一起。但是,既然我們知道波動方程的解不僅僅是各個解的總和,那麼一些計算可能需要使用正確的索爾金引數進行更新。我們的發現最終可能有助於科學家為這些觀測開發更好的誤差模型。
圖片來源:尼克·博克爾曼
量子三元位元
我們的實驗不僅在理論上很有趣,而且在實踐中也可能很有趣。我們希望使用我們的三縫工藝來幫助設計用於量子計算的新工具。
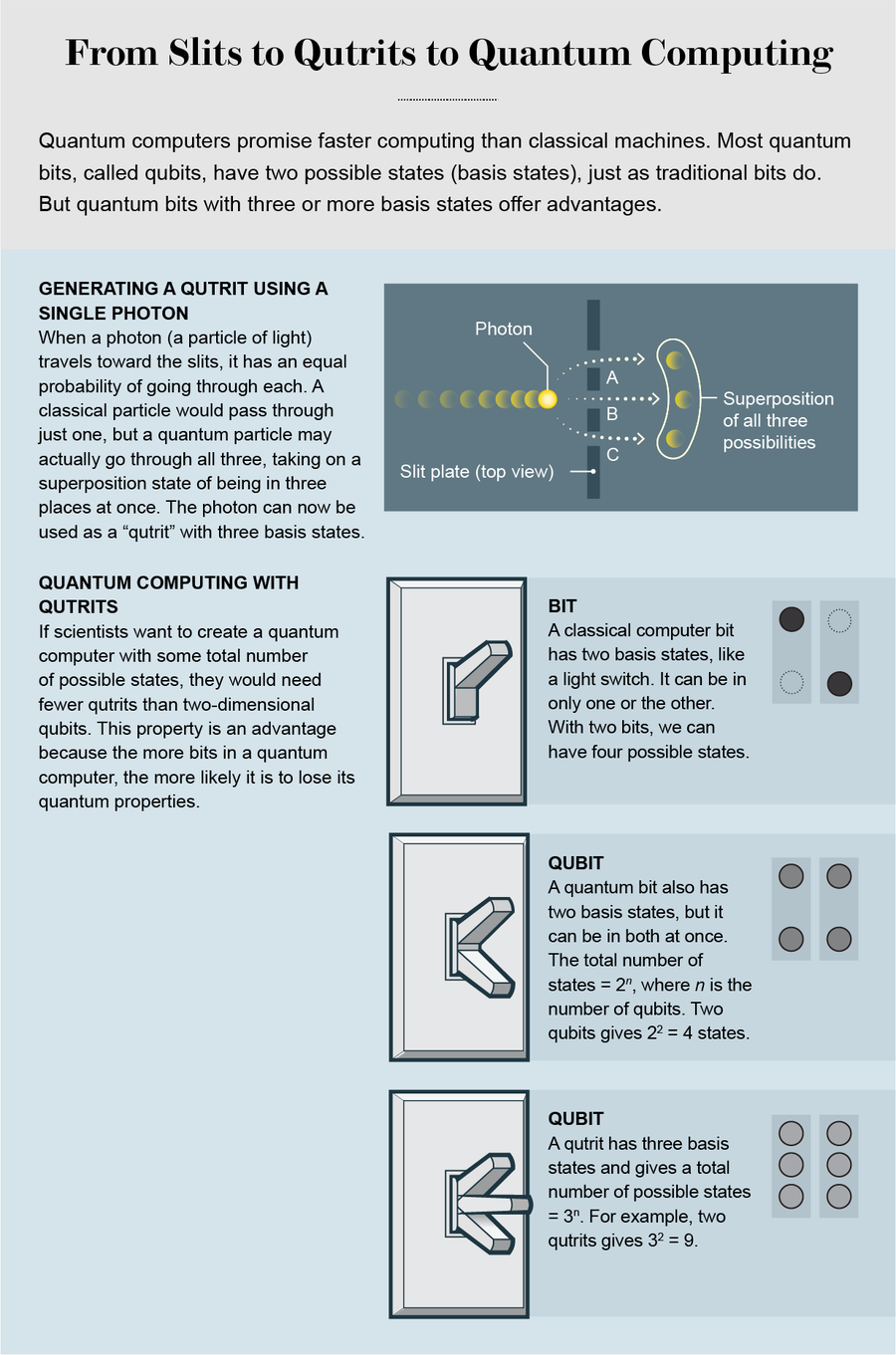
量子計算機利用疊加等量子定律,使計算速度比經典計算機快得多。將傳統的計算機位元想象成一個電燈開關:它可以是“開”或“關”(分別對應於二進位制程式碼中的值1或0)。然而,在量子世界中,開關不必是開或關——它可以兩者都是。在量子位元中,我們定義了一種狀態,該狀態以有限的概率同時處於開狀態和關狀態。這兩種狀態的組合以及每種狀態的機率是疊加的本質。
構成疊加態的兩種狀態稱為基態。一個普通的量子位元有兩個基態,對於n個量子位元,可以訪問2n種可能的狀態。因此,對於兩個量子位元,有22 = 4種可能的狀態。然而,對於n個經典位元,狀態只發生在2n種可能性中的一種,而對於n個量子位元,所有2n種可能性都可以共存。量子計算的力量來自巧妙設計的量子演算法,這些演算法可以在執行期間利用疊加態,並以比經典計算機快指數級的速度執行某些型別的操作。
然而,為了實現這個目標,我們需要相當多的量子位元——當然不僅僅是兩個。社群中許多人已經開始努力實現的一個數字是n = 50,這為量子演算法提供了許多有趣的可能性。
有了50個量子位元,我們就有250種可能的狀態可用於量子運算。最近,谷歌聲稱它透過在54量子位元量子處理器上成功實現隨機抽樣計算,實現了這個里程碑。然而,獲得大量量子位元說起來容易做起來難。我們放在一起的量子位元越多,它們失去疊加的特殊量子能力並崩潰回正常的經典位元的可能性就越大。當量子位元與外部環境相互作用並失去“相干性”時,就會發生這種情況。當我們嘗試將更多量子位元放入相干疊加態時,長時間維持這種狀態變得越來越困難。這很像把人放到一個房間裡參加聚會。如果你在一個100平方英尺的房間裡有10個人,那麼有足夠的空間讓他們共存而不會進入彼此的空間。如果我們將人數增加到30人,就會開始出現擁擠,這會導致普遍失去和平共處。量子位元也會發生同樣的事情。
通常策略的一種替代方案是增加每個量子位元的維度,而不是試圖在同一空間中容納更多量子位元。為了瞭解為什麼這會有所幫助,讓我們回到一個基本的數學問題
23是多少?答案當然是 8 (2 × 2 × 2 = 8)。
現在,32是多少?這裡的答案是 9 (3 × 3 = 9)。
這些結果是同一數量級的——非常接近。因此,如果我們使用兩個三元量子位元(即三維量子位元)而不是三個量子位元,我們將可以訪問相似數量的可能狀態。因此,與其嘗試增加指數,為什麼不嘗試改變底數呢?如果我們增加基態的數量,我們將需要更少的位元來實現相同的目標。這種認識定義了更高維度量子系統中的研究。
我們的策略還有另一個好處:我們不再受二進位制程式碼的約束。考慮一場足球比賽的結果。通常我們認為有兩種結果,“勝”和“負”,可以使用兩種狀態來指定,所以在量子世界中,一個量子位元就足夠了。如果我們再新增兩種可能的結果,例如“放棄”和“平局”,一個量子位元不足以宣告結果。我們需要兩個量子位元。但是,如果我們有一個四態系統,一個就足夠了。這樣的系統將是一個“四元量子位元”。
因此,更高維度的量子系統或量子數字系統可以在更少的系統中打包更多資訊。從理論上講,這種優勢已被證明在量子計算機的某個目標方面具有優勢——即使用所謂的量子金鑰分發建立防駭客通訊。在這種方法中,雙方建立一個共享的秘密“金鑰”,只有他們可以使用該金鑰來解碼訊息。如果你可以透過增加基態的數量來增加量子位元的維度,那麼結果就是一個更能抵抗某些型別攻擊的金鑰。除了金鑰分發中更高的安全性的可能性之外,量子數字還承諾在真正的隨機數生成中具有更大的隨機性——這是量子計算機的另一個有希望的應用。
儘管有這些好處,但基於量子數字的系統也有一些缺點。實際上很難想出穩定的物理系統,其中所有基態都同樣容易達到。例如,有時系統可能會偏向其最低能量或基態,並且由此產生的計算可能會帶有這種偏差。第二個障礙僅僅是,這條研究路線比量子位元更新,因此為量子數字開發的演算法和工具更少。儘管有很多事情要做,但未解決問題的數量使這項研究令人興奮且潛力巨大。
邁向量子計算機
那麼,我們如何從基本的三縫實驗過渡到工作的三元量子位元系統?第一步是生成單光子。
我們從非常強的雷射束開始,將其照射到特殊的晶體材料上。在某些條件下,大約每108到1010個光子中就有一個在稱為下轉換的過程中分裂成兩個能量較低的光子。子光子總是成對出現。我們使用單光子探測器測量其中一個光子,並且由於我們知道它們是同時產生的,因此該測量預示著另一個光子的存在。然後我們可以使用第二個光子進行實驗。
在我們團隊的工作中,我們研究了“母”光子的特性,以確保子光子共享其特性。母光子 направляется 向三個狹縫,其空間輪廓 затем 模擬三縫輪廓。子光子反過來也攜帶這個輪廓。光子進入疊加態,這給了我們一個“空間箱”三元量子位元,其三個基態是三個狹縫位置。
儘管如此,我們建立的這個三元量子位元與功能性量子計算機所需的三元量子位元還相差甚遠。我們需要使用我們的狹縫系統生成大量的三元量子位元,然後將它們饋送到具有所謂門操作的架構中,這些門操作能夠使用三元量子位元來執行計算。這個領域是我團隊當前工作的重點。我們必須設計完成這種操作所需的特定光學元件,然後將所有東西小型化,使其能夠定義一個工作計算機系統。
因此,三縫代表了物理學研究的陰陽兩面——既是基礎的又是功能性的。我們對疊加原理及其首次測量的修正項的研究探索了物理學的最基本概念。與此同時,基於三縫的量子數字代表了在邁向更高維度量子計算和量子通訊方面的技術壯舉。事實證明,這個最著名的物理實驗仍在提供新的見解和可能性。”

