2020年,我們中的一人,託尼,邀請我們中的另一人,馬可,來到他在巴塞羅那附近卡斯特爾德費爾斯的 photonics 科學研究所的辦公室。“我想和你討論一個問題,”託尼開始說。“這是米格爾和我多年來一直試圖解決的問題。” 馬可面露好奇,於是託尼提出了問題:“標準量子理論在沒有虛數的情況下能行得通嗎?”
虛數,當它們自身相乘時,會產生一個負數。它們最初被哲學家勒內·笛卡爾命名為“虛數”,以區別於他已知和接受的數字(現在稱為實數),實數不具有這種性質。後來,複數,即實數和虛數的和,因其在解決複雜數學問題中的實用性而得到數學家的廣泛接受。然而,它們不是任何基本物理理論方程的一部分——除了量子力學。
最常見的量子理論版本依賴於複數。當我們把理論中出現的數字限制為實數時,我們就得到了一個新的物理理論:實數量子理論。在21世紀的第一個十年裡,幾個團隊表明,這個“實數”版本的量子理論可以用來正確地模擬一大類量子實驗的結果。這些發現使許多科學家相信,實數量子理論可以模擬任何量子實驗。科學家們認為,選擇使用複數而不是實數並不代表一種物理立場;這只是一個數學上的便利問題。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將有助於確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
儘管如此,這個猜想仍未得到證實。它可能是錯誤的嗎?在託尼辦公室的那次談話之後,我們開始了為期數月的反駁實數量子理論的旅程。我們最終提出了一個量子實驗,其實驗結果無法透過實數量子模型來解釋。我們的發現意味著虛數是標準量子理論中必不可少的成分:沒有虛數,該理論將失去預測能力。這意味著什麼?這是否意味著虛數以某種方式存在?這取決於人們對標準量子理論或任何物理理論的要素“存在”的觀念有多認真,而不是將它們僅僅視為描述和預測實驗觀察結果的數學配方。
虛數的誕生
複數可以追溯到16世紀早期,當時義大利數學家安東尼奧·瑪麗亞·菲奧爾向教授尼科洛·豐塔納“塔爾塔利亞”(口吃者)發起了挑戰。在當時的義大利,任何人都可以向數學教授發起“數學決鬥”,如果他們贏了,他們可能會得到對手的工作。因此,數學家傾向於將他們的發現秘而不宣,只在贏得智力之戰時才使用他們的定理、推論和引理。
菲奧爾的導師西皮奧內·德爾·費羅在臨終前給了菲奧爾一個公式,用於求解 x3 + ax = b 形式的方程,也稱為三次方程。菲奧爾憑藉他導師的成就,向塔爾塔利亞提出了30個三次方程,並挑戰他找出每種情況下的 x 值。
塔爾塔利亞在比賽前不久發現了這個公式,解決了這些問題並贏得了決鬥。塔爾塔利亞後來向醫生和科學家吉羅拉莫·卡爾達諾吐露了他的公式,卡爾達諾承諾永遠不會向任何人透露。儘管他發了誓,但卡爾達諾還是想出了該公式的證明並以他的名字發表了。這個複雜的方程包含兩個平方根,因此人們理解,如果根號內的數字是負數,則該方程將無解,因為沒有實數自身相乘會產生負數。
在這些陰謀詭計中,第四位學者拉斐爾·蓬貝利做出了數學史上最著名的發現之一。蓬貝利發現了一些可解的三次方程,但德爾·費羅-塔爾塔利亞-卡爾達諾公式仍然需要計算負數的平方根。然後他意識到,對於所有這些例子,只要他假裝存在一種新型的數字,其平方等於 −1,該公式就會給出正確的解。假設公式中的每個變數都具有 a + √−1 × b 的形式,其中 a 和 b 是“正常”數字,則乘以 √−1 的項被抵消,結果是方程的“正常”解。

來源:Jen Christiansen
在接下來的幾個世紀裡,數學家研究了所有 a + √−1 × b 形式的數字的性質,這些數字被稱為“複數”。在17世紀,被認為是理性科學之父的笛卡爾將這些數字與幾何形狀中不存在的特徵聯絡起來。因此,他將數字 i = √−1 命名為“虛數”,以區別於他所知的正常數字,他稱之為“實數”。數學家今天仍然使用這個術語。
事實證明,複數是一個非常棒的工具,不僅可以用來解方程,還可以簡化經典物理學——20世紀之前發展起來的物理學——的數學。經典理解的光就是一個例子。將光描述為旋轉的複數電場和磁場比描述為振盪的實數電場和磁場更容易,儘管實際上不存在虛數電場。同樣,如果假裝電流具有複數值,則描述電子電路行為的方程更容易求解,引力波也是如此。
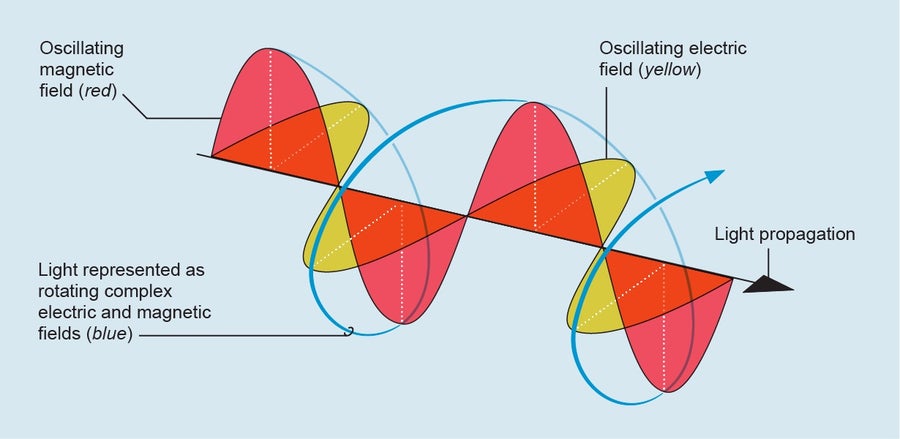
來源:Jen Christiansen
在20世紀之前,所有這些複數運算都被簡單地視為一種數學技巧。最終,任何經典理論的基本要素——溫度、粒子位置、場等等——都對應於實數、向量或函式。量子力學是一種在20世紀早期引入的物理理論,旨在理解微觀世界,它將從根本上挑戰這種狀況。
薛定諤和他的方程
在標準量子理論中,物理系統的狀態由複數向量(具有大小和方向的量)表示,稱為波函式。物理性質,如粒子的速度或位置,對應於複數表,稱為算符。從一開始,這種對複數的深度依賴就違背了物理理論必須用實數量級來表述的根深蒂固的信念。薛定諤方程的作者埃爾溫·薛定諤是最早表達物理學界普遍不滿的人之一。在1926年6月6日寫給物理學家亨德里克·洛倫茲的信中,薛定諤寫道:“這裡令人不快,而且確實直接反對的是複數的使用。Ψ [波函式] 肯定從根本上是一個實函式。”
起初,薛定諤的不安似乎很容易解決:他重寫了波函式,用兩個實向量代替了單個複數向量。薛定諤堅持認為這個版本是“真實”的理論,而虛數僅僅是為了方便。從那以後的幾年裡,物理學家們找到了其他基於實數重寫量子力學的方法。但這些替代方案都從未流行起來。標準的量子理論,憑藉其複數,有一個方便的規則,可以很容易地表示由許多獨立部分組成的量子系統的波函式——這是其他版本所缺乏的特性。
那麼,如果我們將波函式限制為實數並且保留用於組合多部分系統的常用量子規則,會發生什麼?乍一看,沒什麼大不了的。當我們要求波函式和算符具有實數項時,我們最終得到了物理學家通常所說的“實數量子理論”。這個理論類似於標準量子理論:如果我們生活在一個實數量子世界中,我們仍然可以進行量子計算,透過交換量子粒子互相傳送秘密訊息,以及將亞原子系統的物理狀態遠端傳送到洲際距離。
所有這些應用都基於量子理論的反直覺特徵,例如疊加、糾纏和不確定性原理,這些也是實數量子理論的一部分。由於這種公式包含了這些著名的量子特徵,物理學家長期以來一直認為,在量子理論中使用複數基本上是一個方便的問題,而實數量子理論與標準量子理論一樣有效。然而,在2020年秋季的那個早晨,在馬可的辦公室裡,我們開始懷疑這一點。
來源:Jen Christiansen
證偽實數量子理論
在設計一個實驗來反駁實數量子理論時,我們不能對科學家可能使用的實驗裝置做任何假設,因為任何實數量子理論的支持者總是可以挑戰它們。例如,假設我們製造了一種旨在測量光子偏振的裝置。反對者可能會辯稱,雖然我們認為我們測量的是偏振,但我們的儀器實際上探測的是一些其他屬性——例如,光子的軌道角動量。我們無法知道我們的工具是否像我們認為的那樣工作。然而,在不對實驗裝置做任何假設的情況下證偽物理理論聽起來是不可能的。當沒有確定性可以依賴時,我們如何證明任何事情?幸運的是,有一個歷史先例。
儘管阿爾伯特·愛因斯坦是量子理論的創始人之一,但他從未相信我們的世界像該理論所暗示的那樣違反直覺。他認為,儘管量子理論做出了準確的預測,但它一定是更深層次理論的簡化版本,在該理論中,其明顯的悖論式特質將得到解決。例如,愛因斯坦拒絕相信海森堡不確定性原理——它限制了對粒子位置和速度的瞭解程度——是根本性的。相反,他推測,他那個時代的實驗學家由於技術限制而無法制備具有明確定義的位置和速度的粒子。愛因斯坦假設,未來的“經典”理論(一種基本粒子的物理狀態可以完全確定且不基於機率的理論)將解釋所有量子實驗的結果。
我們現在知道愛因斯坦的直覺是錯誤的,因為所有這樣的經典理論都已被證偽。1964年,約翰·S·貝爾表明,一些量子效應無法用任何經典理論來建模。他設想了一種實驗型別,現在稱為貝爾測試,涉及兩位實驗學家,艾麗絲和鮑勃,他們在獨立的實驗室工作。第三個地點的某人向他們每個人傳送一個粒子,他們獨立地測量這些粒子。貝爾證明,在任何具有明確定義的屬性的經典理論(愛因斯坦希望勝出的那種理論)中,這些測量的結果都服從某些條件,稱為貝爾不等式。然後貝爾證明,在某些艾麗絲和鮑勃測量糾纏量子態的設定中,這些條件被違反了。重要的性質是貝爾不等式適用於人們可以想到的所有經典理論,無論多麼複雜。因此,它們的違反反駁了所有此類理論。
此後,在實驗室進行的各種貝爾測試測量到的結果正如量子理論所預測的那樣。2015年,在荷蘭代爾夫特、奧地利維也納和科羅拉多州博爾德進行的貝爾實驗最終做到了這一點,同時彌合了以前實驗留下的所有漏洞。這些結果並沒有告訴我們我們的世界是量子的;相反,它們證明,與愛因斯坦相反,它不能由經典物理學統治。
我們能否設計一個類似於貝爾實驗的實驗,也能排除基於實數的量子理論?為了實現這一壯舉,我們需要設想一個標準量子理論實驗,其實驗結果無法用實數量子理論的數學來解釋。我們計劃首先設計一個思想實驗——一個思想實驗——我們希望物理學家隨後在實驗室中進行。我們認為,如果能夠做到這一點,這個測試應該能夠說服即使是最持懷疑態度的支持者,世界也不是用實數量子理論來描述的。
我們的第一個也是最簡單的想法是嘗試升級貝爾的原始實驗,以便也證偽實數量子理論。不幸的是,2008年和2009年發表的兩項獨立研究——一項由卡羅利·帕爾和塔瑪斯·韋爾泰西進行,另一項由馬修·麥卡格、米歇爾·莫斯卡和尼古拉斯·吉辛進行——發現這行不通。研究人員能夠證明,實數量子理論可以像標準量子理論一樣好地預測任何可能的貝爾測試的測量結果。由於他們的研究,大多數科學家得出結論,實數量子理論是不可反駁的。但我們和我們的合著者證明這個結論是錯誤的。
設計實驗
在我們卡斯特爾德費爾斯對話後的兩個月內,我們的小專案聚集了八位理論物理學家,他們都位於那裡或日內瓦或維也納。雖然我們不能親自見面,但我們交換了電子郵件,每週多次舉行線上討論。正是透過長時間的獨自散步和密集的 Zoom 會議相結合,在2020年11月的一個快樂的日子裡,我們提出了一個標準量子實驗,實數量子理論無法對其進行建模。我們的關鍵想法是放棄標準的貝爾場景,在貝爾場景中,單個源將粒子分發給幾個獨立的參與者,並考慮具有多個獨立源的設定。我們觀察到,在這種物理學家稱之為量子網路的場景中,帕爾-韋爾泰西-麥卡格-莫斯卡-吉辛方法無法重現複數量子理論預測的實驗結果。這是一個有希望的開始,但這還不夠:類似於貝爾對經典理論所取得的成就,我們需要排除任何形式的實數量子理論的存在,無論多麼聰明或複雜,都能夠解釋量子網路實驗的結果。為此,我們需要在量子網路中設計一個具體的思想實驗,並證明標準量子理論的預測不可能用實數量子理論來建模。
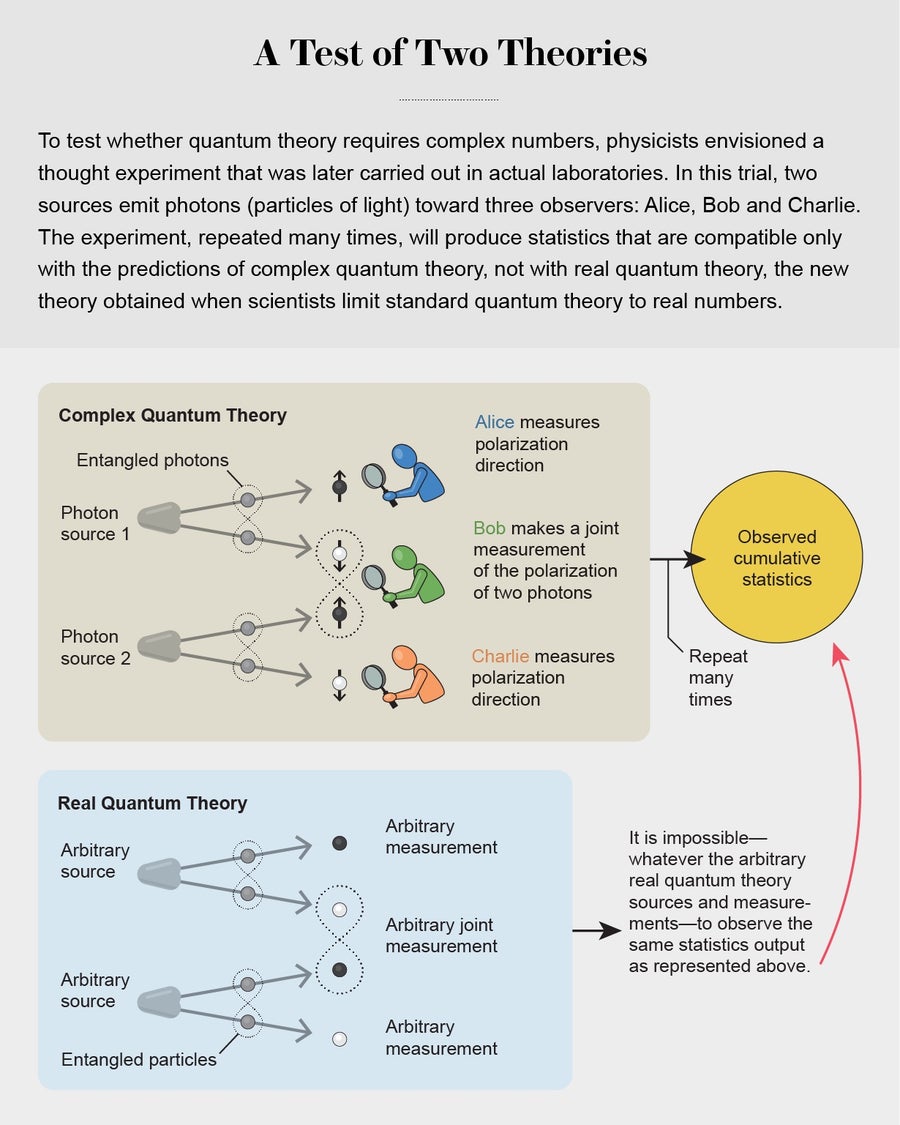
最初我們考慮了涉及六位實驗學家和四個來源的複雜網路。然而,最後,我們決定採用一個更簡單的量子實驗,其中包括三位獨立的實驗人員,分別稱為艾麗絲、鮑勃和查理,以及兩個獨立的粒子源。第一個源發出兩個光粒子(光子),一個給艾麗絲,一個給鮑勃;第二個源向鮑勃和查理髮送光子。接下來,艾麗絲和查理選擇一個方向來測量他們粒子的偏振,結果可能是“向上”或“向下”。與此同時,鮑勃測量他的兩個粒子。當我們一遍又一遍地這樣做時,我們可以建立一套統計資料,顯示測量結果的相關性有多頻繁。這些統計資料取決於艾麗絲和查理選擇的方向。
接下來,我們需要證明觀察到的統計資料無法被任何實數量子系統預測。為了做到這一點,我們依賴於一個稱為自測試的強大概念,該概念允許科學家同時驗證測量裝置和它正在測量的系統。這是什麼意思?想想一個測量儀器——例如,一個體重秤。為了保證它的準確性,您需要用一個經過認證的重量的質量來測試它。但是如何認證這個質量呢?您必須使用另一個秤,它本身也需要認證,依此類推。在經典物理學中,這個過程沒有盡頭。令人驚訝的是,在量子理論中,可以同時認證被測系統和測量裝置,就好像秤和測試質量正在相互檢查校準一樣。
考慮到自測試,我們的不可能證明工作原理如下。我們構思了一個實驗,其中,對於鮑勃的任何結果,艾麗絲和查理的測量統計資料自測試了他們共享的量子態。換句話說,一個人的統計資料證實了另一個人的量子性質,反之亦然。我們發現,與實數量子理論相容的裝置的唯一描述必須恰好是帕爾-韋爾泰西-麥卡格-莫斯卡-吉辛版本,我們已經知道該版本不適用於量子網路。因此,我們得出了我們希望得到的矛盾:實數量子理論可以被證偽。
我們還發現,只要艾麗絲、鮑勃和查理觀察到的任何真實世界測量統計資料都足夠接近我們理想的思想實驗的統計資料,它們就不能用實數量子系統重現。邏輯非常類似於貝爾定理:我們最終推匯出了實數量子理論的貝爾不等式,並證明了複數量子理論可以違反它,即使在存在噪聲和缺陷的情況下也是如此。這種對噪聲的容許性使我們的結果在實踐中可測試。沒有實驗學家能夠完全控制他們的實驗室;他們能期望的最好結果是製備近似於他們目標的量子態,並進行近似於他們預期進行的測量,這將使他們能夠生成近似於預測的相同測量統計資料。好訊息是,在我們的證明中,證偽實數量子理論所需的實驗精度雖然要求很高,但在當前技術的範圍內。當我們公佈我們的結果時,我們希望這只是時間問題,總會有人在某個地方實現我們的願景。
這件事發生得很快。在我們公開我們的發現僅僅兩個月後,上海的一個實驗小組報告說,他們使用超導量子位元——由量子粒子製成的計算機位元——實現了我們的思想實驗。大約在同一時間,深圳的一個小組也聯絡我們,討論使用光學系統進行我們的思想實驗。幾個月後,我們讀到了另一個光學版本的實驗,也是在上海進行的。在每種情況下,實驗人員都觀察到了實數量子理論無法解釋的測量結果之間的相關性。雖然仍有一些實驗漏洞需要處理,但總而言之,這三個實驗使實數量子假設非常難以維持。
量子未來
我們現在知道經典理論和實數量子理論都無法解釋某些現象,那麼接下來會發生什麼?如果未來提出量子理論的替代版本作為標準理論的替代方案,我們可以使用類似的技術來嘗試排除它們。我們能否更進一步,證偽標準量子理論本身?
如果我們這樣做了,鑑於我們目前缺乏替代方案,我們將沒有任何微觀世界的理論。但物理學家並不相信標準量子理論是正確的。原因之一是它似乎與我們的另一個理論——廣義相對論——相沖突,廣義相對論用於描述引力。科學家們正在尋找一種新的、更深層次的理論,可以調和這兩種理論,甚至可能取代標準量子理論。如果我們能夠證偽量子理論,我們或許能夠指出通往更深層次理論的道路。
與此同時,一些研究人員正在試圖證明,除了量子理論之外,沒有其他理論可以做到這一點。我們的合著者之一米里亞姆·韋倫曼與羅傑·科爾貝克合作,認為有可能透過合適的類貝爾實驗來排除所有替代物理理論。如果這是真的,那麼這些實驗將表明,量子力學確實是唯一與實驗觀察結果相容的物理理論。這種可能性讓我們不寒而慄:我們真的可以希望證明量子理論是如此特殊嗎?
編者注(4/6/23):在釋出後,修訂了“什麼是虛數?”框,以更正有理數如何包含整數的描述。這篇文章此前於3月24日進行了修訂,在開篇插圖中添加了標題,以更正兩個方程式。

