2007年,亞歷山大·沙波瓦洛夫為第六屆國際柯爾莫哥洛夫數學競賽提出了一個不尋常的硬幣稱重問題 [5]。
一位法官面前有 80 枚看起來相同的硬幣,他知道其中有兩枚或三枚假幣。所有真幣重量相同,所有假幣重量也相同,但假幣比真幣輕。
一位律師知道恰好有三枚假幣,並且知道是哪三枚。律師必須使用天平來說服法官,確實有三枚假幣,並且不可能只有兩枚假幣。她受合同約束,不得洩露任何關於特定硬幣的資訊。她應該如何進行?
為什麼這個問題如此不尋常?讓我們回顧一下歷史。第一個硬幣稱重問題出現在 1945 年左右 [6, 7]。在所有這些問題中,目標僅僅是在許多真幣中找到一枚假幣。在那之後,出現了許多推廣:新版本的假幣問題包括找到多枚假幣,區分任意重量的硬幣等等。然而,所有這些問題的附加目標都是儘量減少定位假幣所需的稱重次數 [2]。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
沙波瓦洛夫的難題是第一個將注意力從消除硬幣隱私轉移到維護硬幣隱私的問題。這個難題非常重要且具有現代意義;像許多其他“硬幣稱重”問題一樣,它不是關於硬幣,而是使用硬幣來模擬想法,並建立真實生活中的隱私問題及其潛在解決方案的簡化版本。
簡化版本
讓我們考慮一個更簡單的沙波瓦洛夫難題版本,以便入門
示例 1。 在與之前類似的情況下,律師想向法官證明假幣的數量正好是兩枚,而不是一枚。
策略 1。 律師將硬幣分成兩堆,每堆 40 枚,以便每堆正好包含一枚假幣。然後,她將這兩堆硬幣放在天平的不同托盤中。
天平平衡,這意味著兩個托盤中假幣的數量相同。因此,假幣的總數是偶數,在本例中,正好是 2 枚。對於任何特定的硬幣,法官都無法明確地說出它是真幣還是假幣;因此,我們成功地完成了任務。
在繼續之前,讓我們介紹一些符號。我們將用 t 表示硬幣總數,用 ƒ 表示假幣的實際數量,用 d 表示我們試圖證偽的假幣數量。
我們還想為一種策略或一系列稱重新命名,在這些稱重之後,法官對任何特定硬幣的真偽一無所知。Knop [4] 建議將此類策略稱為“沙波瓦洛夫策略”,以紀念該難題的設計者。其中一位作者 [3] 使用了“不洩露”這個名稱。我們不喜歡“不洩露”這個名稱,因為我們計劃表明所有策略都會洩露一些資訊。我們喜歡“沙波瓦洛夫”這個名稱,但我們也希望有一個描述性的名稱。
定義 1。 我們將一組稱重或一種策略稱為“謹慎”策略,在這種策略中,不會洩露關於任何特定硬幣的資訊。否則,我們將這組稱重稱為“不謹慎”策略。
目前,我們只關心謹慎(沙波瓦洛夫)策略。如果 ƒ 和 t 有一個公約數 m ,但 m 不能整除 d,則可以推廣策略 1
策略 1*。 律師將硬幣分成 m 個相等的組,每組包含 ƒ/m 枚假幣,並證明所有組的重量都相等。
現在我們可以回到最初的難題並討論其解決方案。
原始問題的解決方案
受到前一個示例中使用的策略的啟發,律師可以嘗試將 80 枚硬幣分成三組,每組包含一枚假幣。顯然,80 不能被 3 整除,所以她將硬幣分成三個儘可能大的相同大小的組:每組 26 枚,每組一枚假幣。律師使用天平進行兩次稱重,向法官證明所有三組 26 枚硬幣的重量都相同。法官可以得出什麼結論?他可以得出結論,要麼有 3 枚假幣——每組一枚,要麼有 2 枚假幣,並且它們在剩下的 2 枚硬幣組中。不幸的是,這種策略不足以向法官證明正好有 3 枚假幣。律師決定不放棄,並以下列方式調整策略
策略 2。 律師首先證明包含一枚假幣的 26 枚硬幣的三組重量相同。她繼續將剩餘組中的一枚硬幣與不在剩餘組中的一枚真幣進行比較。
該策略證明假幣的數量必須是 3 枚,而不是 2 枚。然而,這種策略是不謹慎的——我們將其留給讀者來驗證這兩個斷言。總的來說,想出這個問題的解決方案已被證明非常棘手。大多數提出的策略都包含一些細微的缺陷,要麼未能排除 2 枚假幣的可能性,要麼至少洩露了一枚硬幣的身份。
現在我們將介紹來自競賽的官方(謹慎)解決方案,並再次請讀者對其進行分析。
策略 3。 律師將所有硬幣分成 5 堆:A 和 B 各有 10 枚硬幣,C、D 和 E 各有 20 枚硬幣,以便三枚假幣分別在 A、D 和 E 堆中。然後,律師進行三次稱重。第一次稱重,她將 A + C 與 B + D 進行比較,天平平衡。第二次稱重,她將 A + B 與 E 進行比較,天平再次平衡。最後一次稱重,她將 C + D 與 A + B + E 進行比較,並表明第二個托盤更輕。
現在我們為這個問題提供另一種謹慎策略。
策略 4。 律師將所有硬幣分成九堆:A1、B1、C1、A2、B2、C2、A3、B3 和 C3,大小分別為 24、1、2、24、1、2、23、2 和 1。律師證明 A1 + B1、A2 + B2 和 A3 + B3 在天平上相互平衡。此外,她還表明 B1 + C1、B2 + C2 和 B3 + C3 的重量相同。
再一次,我們將其留給讀者來證明假幣有三種不同的分佈方式
每組 A1、A2、A3 (大小分別為 24、24、23) 中各有一枚假幣
每組 B1、B2、B3 (大小分別為 1、1、2) 中各有一枚假幣
每組 C1、C2、C3 (大小分別為 2、2、1) 中各有一枚假幣。
在每種情況下,我們都排除了存在兩枚假幣的可能性,並且沒有洩露任何特定硬幣的身份。
在 Knop 的文章 4 (俄語)中檢視更多不足和正確的解決方案示例。
謹慎的硬幣稱重
最初的難題很棘手,但我們已經設法演示了兩種解決方案。是否總是可以找到尊重每枚硬幣隱私的解決方案?或者,在我們新的定義中,是否總是可以找到一組謹慎的稱重?
讓我們指出一個微不足道的事實,即如果 ƒ = 0 或 ƒ = t (因此律師必須向法官證明所有硬幣都是真幣/假幣),那麼每枚硬幣的隱私都必然會因所證明的陳述而被侵犯。
為了防止洩露任何給定硬幣的身份,我們將只考慮 0 < ƒ < t 的情況,因此我們試圖證明的陳述本身就是謹慎的。然而,正如以下引理所證明的那樣,在這種情況下,並非總是可以得到一組謹慎的稱重。
引理 1。對於 t > 1 且 ƒ = 1 ,不可能有謹慎策略。
證明。 假設存在這樣一種策略,並且律師說服法官假幣的總數為 1 枚。現在考慮任何一次稱重。如果天平平衡,那麼兩個托盤上的硬幣必然都是真幣。如果天平不平衡,那麼我們知道較重託盤上只有真幣。在任何一種情況下,一些硬幣都被證明是真的,因此該策略是不謹慎的。
我們將其留給讀者來證明,對於以下引數,也不可能得到謹慎策略。
• t > 1 且 ƒ = t − 1
• ƒ = 2 且 d = 0。
揭示因子和係數
考慮策略 1,即簡化的案例,其中律師將硬幣分成兩組,每組 40 枚。假設法官知道有 2 枚假幣。在稱重之前,他猜對一枚假幣位置的機率是多少?僅僅是 80 分之 2。稱重後,法官知道每組 40 枚硬幣中都有一枚假幣,因此他找到一枚硬幣的機率是 40 分之 1——與之前相同。
儘管看起來好像沒有洩露任何資訊,但事實恰恰相反。在稱重之前,這兩枚假幣可以是 80 枚硬幣中的任何一枚,這些假幣的等可能分佈的數量為 (802) = 3160。稱重後,每堆 40 枚硬幣中都有一枚假幣,可能性數量減少到 (401)2 = 1600。在 [1] 中討論了在成功策略之後嘗試猜測單枚假幣位置的一般挑戰。
我們想引入揭示因子和揭示係數的概念來量化這種觀察結果。在稱重之前,如果法官知道假幣的數量正好是 ƒ 枚,那麼任何 ƒ 枚硬幣的集合都可能是假幣的集合。等可能性的數量為 (tƒ),我們稱此值為“舊可能性”。稱重後,可能性集合減少,因此並非任何任意 ƒ 枚硬幣組都可能是假幣的集合。我們將在稱重完成後可能成為假幣的 ƒ 枚硬幣集合的數量稱為“新可能性”。
定義 2。 我們將成功策略之後舊可能性數量與新可能性數量的比率稱為揭示因子。我們將其表示為 X
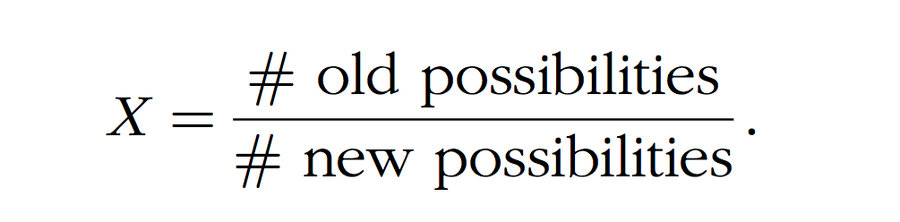
我們還想引入 [3] 中使用的“揭示係數”的概念。揭示係數是在證明正好有 ƒ 枚假幣的過程中洩露的資訊部分
定義 3。 揭示係數,用 R 表示,定義為 1 − 1/X
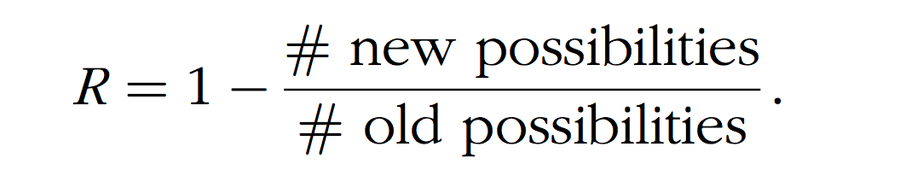
一種幾乎不洩露假幣確切位置資訊的策略對應於更高數量的新可能性。由此可見,我們希望揭示係數和揭示因子都儘可能小,以最大限度地減少資訊傳遞。
在策略 1 中,揭示因子 X 為 3160/1600 = 1:98。揭示係數 R 為 ( 3160 − 1600 ) / 3160 ≈ 0:494,略小於一半。策略 3 和策略 4 的揭示因子的計算更加複雜,留給讀者完成。答案分別約為 10.27 和 6.20。
不同的策略洩露不同數量的資訊
假設我們有 80 枚硬幣,我們想證明有 4 枚假幣而不是 3 枚;即,t = 80,ƒ = 4,d = 3。我們可以使用策略 1* 來進行:將所有硬幣分成四堆,每堆 20 枚,每堆包含一枚假幣。證明所有堆的重量相同告訴法官假幣的數量必須是 4 的倍數,我們就完成了。但是,我們可以產生另一種謹慎策略:將硬幣分成兩堆,每堆 40 枚,每堆放入兩枚假幣。在比較這兩堆硬幣後,法官知道假幣的數量是偶數。這兩種策略都是謹慎的,但揭示因子和係數是不同的,我們將其留給讀者檢查。
第二種策略的揭示性明顯較低;在這種情況下,將所有硬幣分成更少的等效堆顯然更可取。
揭示因子/係數可以為謹慎策略和不謹慎策略定義。令人驚訝的是,我們經常看到不謹慎策略比謹慎策略洩露的資訊更少。讓我們回到最初的問題及其“錯誤”的,或者說是不謹慎的解決方案,策略 2 中描述的解決方案。在稱重後,法官知道 3 枚真幣的位置。其他硬幣分為 3 組,分別為 26、26 和 25 枚硬幣,每組包含一枚假幣。我們將其留給讀者來檢查揭示因子 X ≈ 4:86。儘管此策略是不謹慎的,並且 3 枚真幣的隱私受到侵犯,但它比謹慎策略 3 和策略 4 的揭示性更低,後兩者的揭示因子分別為 10.27 和 6.20。在某種程度上,被暴露為真幣的三枚硬幣有效地“犧牲”了它們的隱私,以使其他希望保持隱藏的硬幣更加安全。
最優性證明
在這裡,我們想展示某些引數的謹慎策略的最優性證明。即,我們考慮 t = 2k、ƒ = 2 和 d = 1 的情況,其中 k 是某個正整數 k > 1。我們已經討論過使用一次稱重的策略(參見策略 1*):將所有硬幣分成大小為 k 的兩堆,將假幣放入單獨的堆中,並比較這兩堆硬幣。
似乎很明顯,這是“最不洩露”或最優的策略,但我們仍然需要證明。首先,我們引入更多定義和符號。在任何稱重過程中,硬幣出現在左托盤上用 L 表示,硬幣出現在右托盤上用 R 表示,未參與的硬幣(留在稱重之外的硬幣)用 O 表示。
在所有稱重之後,每枚硬幣的路徑都可以描述為 L、R 和 O 的字串。
定義 4。與每次稱重中給定硬幣的位置相對應的 L、R 和 O 字串稱為硬幣的“路徑”。
給定路徑 ∂,我們將具有此路徑的所有硬幣的集合表示為 ∂,並將此集合的大小表示為 ∣∂∣。我們將介紹路徑上的對合運算,稱為共軛
定義 5。 給定路徑 ∂,“共軛路徑”,用 −∂ 表示,是唯一的路徑,其中所有 R 都替換為 L,所有 L 都替換為 R。
請注意,這是一個對合運算,因為 =∂ = ∂。此外,唯一的自共軛路徑是 O 的字串。在稱重之後,我們可以根據路徑將所有硬幣分成組。
在以下初步引理中,t 不必是偶數。
引理 2。如果 ƒ = 2 且 d = 1 ,則謹慎策略的路徑集合具有以下性質:如果存在具有路徑 ∂ 的硬幣,則存在具有路徑 −∂ 的硬幣。此外,沒有具有自共軛路徑的硬幣。此外,所有稱重都是平衡的。
證明。 所有稱重都必須是平衡的,否則較重託盤必須僅包含真幣,並且該策略是不謹慎的。由此可見,兩枚假幣在任何時候都不能在同一個托盤中。此外,如果一枚假幣在稱重期間在一個托盤中,則另一枚假幣必須在另一個托盤中以使其平衡。這意味著假幣具有共軛路徑。
由於上述條件,如果存在具有路徑 ∂ 的硬幣,並且沒有具有路徑 −∂ 的硬幣,則 ∂ 中的所有硬幣必然都是真幣。
如果一枚硬幣未參與任何測量,並且所有稱重都是平衡的,那麼我們尚未證偽只有一枚假幣的可能性。因此,不能有任何具有自共軛路徑的硬幣。
現在我們準備證明偶數枚硬幣的最優性定理。
定理 3。 如果 t 為偶數,ƒ = 2 且 d = 1 ,則策略 1 是任何可能策略中最不洩露的策略。
證明。 所有硬幣都根據相同的路徑被劃分為組,並且所有路徑都透過共軛進行配對。路徑集合為 ( ∂j∂j) = 1, 2, 3....如果一枚假幣屬於 ∂j,則另一枚假幣必須屬於 ∂j。這意味著新可能性的總數為
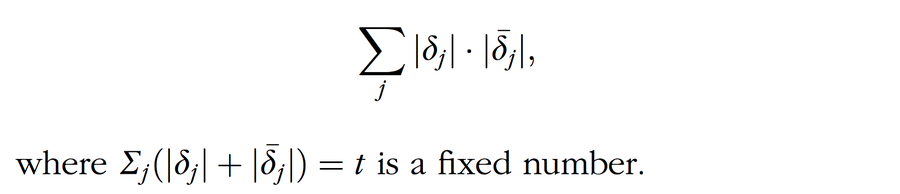
標準代數論證表明,當恰好存在一個路徑對,其中兩個路徑的大小相等時,新可能性的數量最大化。
一個奇特的案例:奇數 t 的情況
我們想討論更復雜情況下的最優性:當硬幣總數為奇數、ƒ = 2 且 d = 1 時。以下引理的證明可以在 [1] 中找到。
引理 4。對於給定引數的謹慎策略必須生成至少 6 個不同的路徑。在這些路徑中,將至少有 3 個共軛對;此外,每對中兩組硬幣的數量必須具有不同的奇偶性。
現在我們將提供更多謹慎策略不存在的示例,再次將證明外包給 [1]。
推論 5。對於 ƒ = 2 且 d = 1,當 t = 3、t = 5 或 t = 7 時,不可能有謹慎策略。
當 t > 7 時會發生什麼?透過修改策略 4,我們可以建立一個適用於奇數 t > 7 的謹慎策略。
策略 4*。 考慮大小分別為 ⌊ t / 2 ⌋ − 2 和 ⌊ t / 2 ⌋ − 3 的堆 A 和 Ā。堆 B 和 B 的大小分別為 1 和 2。堆 C 和 C 的大小分別為 2 和 1。律師將兩枚假幣分配到堆 A 和 A、B 和 B 或 C 和 C 中。
此策略進行兩次稱重。在第一次稱重中,律師將屬於 A 和 B 的 ⌊ t / 2 ⌋ − 1 枚硬幣與屬於 A 和 B 的 ⌊ t / 2 ⌋ − 1 枚硬幣進行比較。在第二次稱重中,她將屬於 B 和 C 的三枚硬幣與 B 和 C 中相同數量的硬幣進行比較。
引理 6。對於 ƒ = 2 且 d = 1,當 t 為奇數且 t > 7 時,策略 4* 是謹慎的。
證明。 所有硬幣都在天平上,並且所有稱重都是平衡的。這意味著必然有兩枚假幣。
由於假幣可以屬於具有共軛路徑的任何一對組,因此沒有洩露任何關於特定硬幣的資訊。
引理 7。如果 t 為奇數,ƒ = 2 且 d = 1 ,則策略 4* 是最不洩露的策略。
該證明與定理 3 的證明類似,可以在 [1] 中找到。
結論
假幣真的需要在法庭上獲得律師的保護嗎?很可能不需要。但是數學家以將難題簡化為更簡單、更易於管理的問題為生。簡而言之,我們的討論表明,從資料庫收集聚合資訊會在過程中洩露一些額外的資訊;本文是我們嘗試量化洩露多少資訊的嘗試。
參考文獻
[1] N. Diaco, T. Khovanova, Weighing Coins and Keeping Secrets, arXiv:1508.05052, (2015).↩
[2] R. K. Guy and R. J. Nowakowski, Coin-weighing problems, Amer. Math. Monthly, 102 (1995), 164–167.↩
[3] T. Khovanova, Unrevealing Coin Weighings, available at http:// blog.tanyakhovanova.com/2009/08/unrevealing-coin-weighings/.↩
[4] K. Knop, The mystery of fake coins, Matematika, N8 (2008), 29–31 (in Russian).↩
[5] Kolmogorov Math Tournaments, http://cdoosh.ru/kolm/kolm.html.↩
[6] E. V. Newbery, The penny problem, Note 2342, Math. Gaz., 37 (1953) 130.↩
[7] B. L. Schwartz, Letter: Truth about false coins, Math. Mag., 51 (1978) 254.↩
[8] Y. Zhang, Coins and Low-Knowledge Proofs, Concrete Nonsense blog, available at https://concretenonsense.wordpress.com/2009/ 12/17/m-3-coins-and-low-knowledge-proofs/.↩
