宇宙中最強的力被稱為強力,這很貼切。我們永遠無法親眼目睹它可怕的力量,因為它只在亞原子距離範圍內起作用,在那裡它將夸克束縛在質子和中子內部,並將這些核子結合成原子核。在自然的四種基本力中,強力無疑是最強大的——它比引力強 100 萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬萬倍。它也是最神秘的。
儘管大致瞭解強力與其他力相比如何,但科學家們並不確切知道強力有多強。其他三種力——引力、電磁力和弱核力(負責某些放射性)——的測量要好得多。例如,電磁力的強度,用其“耦合常數”表示,其測量精度與紐約和洛杉磯之間的距離相同,誤差在幾根頭髮的寬度之內。然而,強力的耦合常數,稱為 αs(“阿爾法 s”),是這些量中最不為人所知的。對 αs 的最佳測量精度比電磁測量的精度差 1 億倍。
即使是這種程度的(不)確定性也僅在強力理論的最簡單領域中已知,即僅在自然界中一些最稀有和最極端事件中涉及的極高能量下。在與我們周圍世界相關的較低能量下,強力透過變得真正強烈而名副其實,並且關於該範圍內 αs 的具體資訊很少。直到最近,還沒有人對這個尺度的 αs 進行任何實驗測量。對其值的理論預測毫無幫助,涵蓋了從零到無窮大的整個範圍。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
珍·克里斯蒂安森
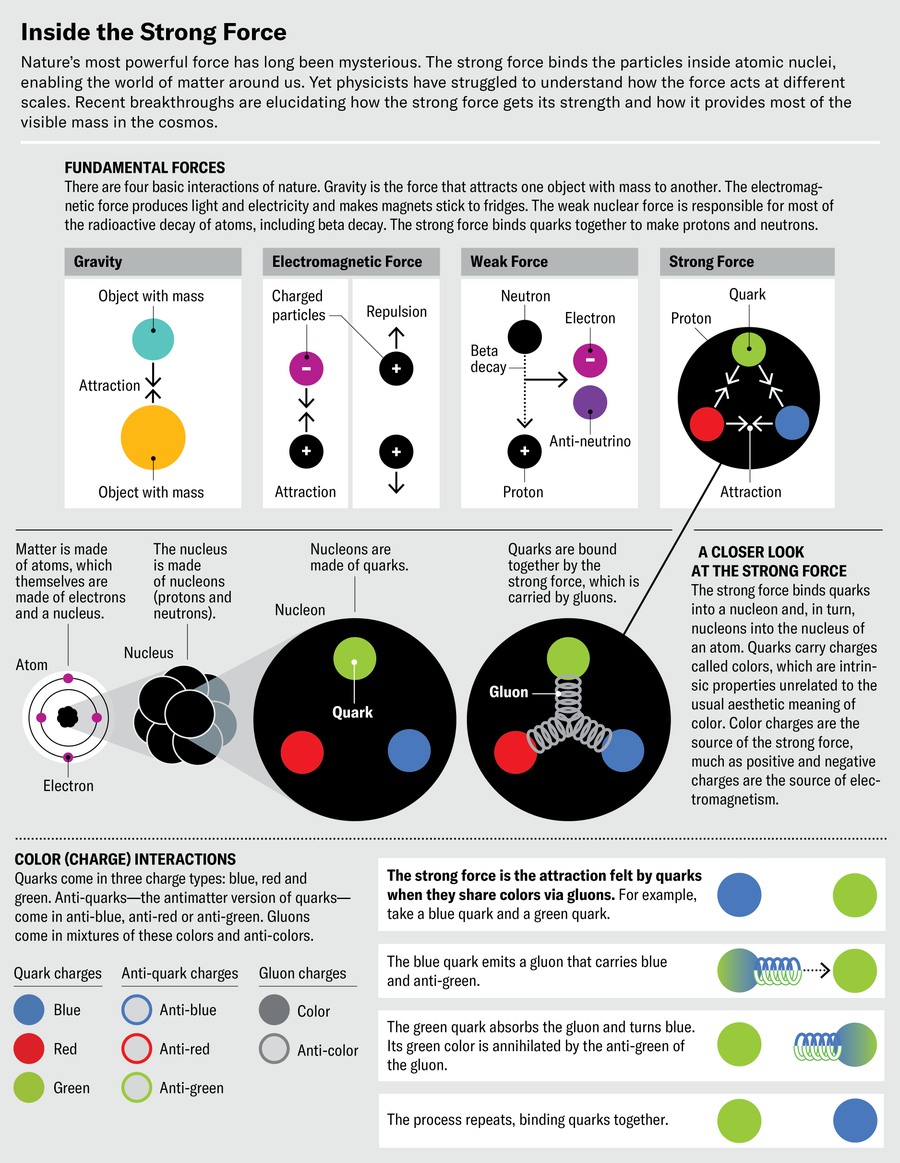
強力的強大使得在很多方面都難以研究它。描述其工作原理的理論,稱為量子色動力學,非常複雜,我們無法使用它來進行直接計算或精確預測。這種複雜性的原因之一是強力的載體——一種稱為膠子的粒子——與自身相互作用。相比之下,電磁學很簡單,因為它的載體光子是不帶電荷的。但膠子攜帶強力的電荷版本,稱為色荷,其自相互作用很快就會失控。因此,儘管強力對核物理和構建物質世界非常重要,但研究人員並非完全喜愛它。相反,許多人將強力真正強大的領域視為“禁地”(Terra Damnata),一個不惜一切代價也要避免的領域。
然而,理解強力對於解釋我們周圍物質的複雜性至關重要。事實上,強力佔可見宇宙中約 99% 質量的來源。(剩下的 1% 來自希格斯玻色子。)而現在,經過半個世紀的努力,科學家們終於開始揭示強力的一些秘密。我們中的一位(德厄爾)最近首次測量了 αs 在禁地內如何變化,我們中的兩位(布羅德斯基和羅伯茨)獨立開發了新的理論預測來解釋這些資料。禁地看起來比以往任何時候都更受歡迎。現在我們可以探索這片領域,我們有望學到更多。我們終於有能力從第一原理分析計算量子色動力學的各個方面。此外,探索強力的這個範圍可能有助於我們理解宇宙的擬議統一理論,以及空間和時間中存在多少維度的問題。

磁鐵引導粒子透過托馬斯·傑斐遜國家加速器實驗室 (Jefferson Lab) 的連續電子束加速器設施 (CEBAF)。
圖片由傑斐遜實驗室提供
如果 αs 是一個常數,它怎麼會變化呢?答案與量子環的概念有關,也稱為真空極化。量子理論揭示,空間的“真空”實際上充滿了微小的粒子,這些粒子不斷出現和消失在波動的雲中。與這些虛粒子的相互作用會導致力偏離其經典行為,因為所謂的量子環。當這個概念首次被引入時,量子環是一個令人不快的意外,因為它們預測了無限量——這是一個明顯的跡象,表明有問題。但最終,物理學家們弄清楚瞭如何馴服這些無限性,並將量子環的所有修正都吸收到描述力載體的方程中。因此,在量子色動力學 (QCD) 中,量子環修正影響膠子的行為,並決定 αs 隨夸克之間距離的變化量。由於量子環的這種新的距離依賴性存在於耦合常數中,這些量失去了它們的常數性。因此,我們從現在開始將其稱為“耦合”。
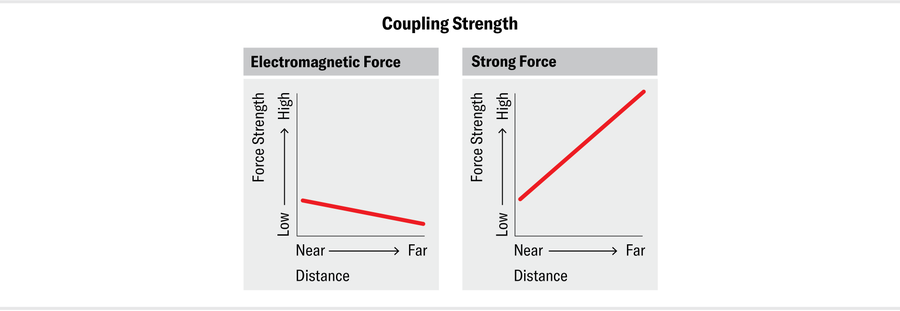
對於大多數力,耦合隨距離變化緩慢。例如,從人類探測到的最小尺度到日常尺度,電磁耦合 αem 僅下降其值的約 10%。然而,對於強耦合 αs,變化是巨大的:即使在物理學家可以舒適地計算 αs 的領域內(即,遠離禁地),其值也變化了幾個數量級。另一個更重要的區別是,電磁耦合隨著距離的增加而減小。然而,對於強力,αs 隨著距離的增加而增加。如果您試圖將質子內的兩個夸克彼此拉開,它們之間的吸引力就會變得更強。事實上,它增長得如此強大,以至於幾乎不可能將夸克從彼此剝離開來——強力將它們“禁閉”起來,您永遠找不到單個的夸克。同樣的規則適用於夸克和膠子之間以及膠子和膠子之間的相互作用。另一方面,這些相互作用在短距離內很弱:您越靠近夸克,它的束縛就越鬆散。αs 在短距離處的小值被稱為漸近自由,其在 20 世紀 70 年代的發現最終為其先驅贏得了 2004 年諾貝爾物理學獎。
珍·克里斯蒂安森
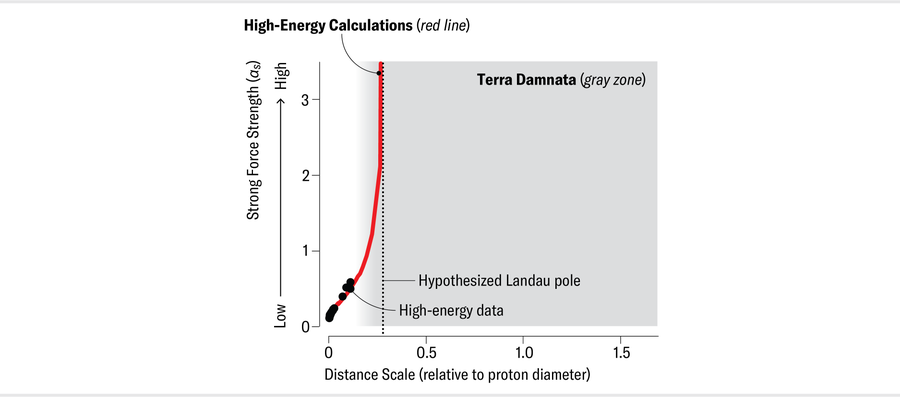
在短距離處,αs 很小,物理學家可以使用與我們用於電磁力和弱力相同的方法進行計算。但這些方法不適用於較長距離的 QCD——例如,質子的大小。按照日常標準,這個長度仍然非常小(質子的大小是原子的五萬分之一,半徑約為十億分之一米的百萬分之一)。然而,它代表了粒子物理學中的一個廣闊領域。問題在於 αs 增長得太快。在我們能夠達到費米之前,αs 變得太大,標準計算方法無法適用。這就是為什麼(甚至不是很)長距離領域變成了禁地。
珍·克里斯蒂安森
由於通常的計算方法不可用,物理學家嘗試了其他策略,但它們要麼未經充分測試,要麼不精確,並預測 αs 的長距離極限可能介於零和無窮大之間。通常的短距離計算方法預測 αs 在長距離範圍內的值為無窮大。但是,這種無窮大,在物理學家列夫·朗道之後被稱為朗道極點,僅表明計算方法失敗,而不是告訴我們關於強力的資訊。確定 αs 在距離處的作用至關重要。
許多物理學家廣泛努力的突破終於出現了。這個故事分三個階段展開,我們中的一位參與了每個階段。
第一步是幸運的。在 20 世紀 90 年代後期,德厄爾是弗吉尼亞州托馬斯·傑斐遜國家加速器實驗室(傑斐遜實驗室)的一名博士生,該實驗室擁有一臺粒子加速器。他的測量跨越了短距離和禁地之間的過渡。當時,他知道朗道極點,但不知道它是假的。他感到困惑的是,在 αs 應該明顯變化的距離處(或者他認為應該如此),似乎什麼都沒有發生。資料完全平滑,沒有他被引導期望的爆發跡象。這些測量結果似乎並沒有困擾更有經驗的科學家,他們已經習慣於在這個區域收集資料,而且學生在用盡歡迎之前只能提出這麼多幼稚的問題。因此,他將這個問題新增到他不瞭解世界的長長清單中,以便(可能)以後回答,然後繼續前進。
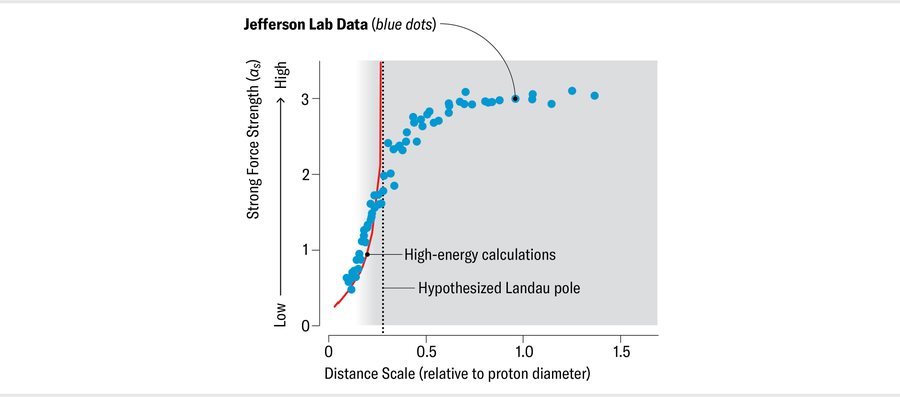
珍·克里斯蒂安森
幾年後,他使用他的資料和傑斐遜實驗室的其他測量結果來測量一個稱為比約肯積分的量,該積分以詹姆斯·比約肯的名字命名,他是強力研究的先驅之一。比約肯積分與質子和中子內部夸克自旋的方向有關,並且作為獎勵,只要您遠離禁地,它也提供了一種相對容易的方法來計算 αs。因此,德厄爾能夠在短距離的可靠領域測量 αs。出於好奇心和喜歡實驗的傾向,他還檢查了該公式對長距離的預測。這個實驗只是為了好玩,他非常清楚他不應該認真對待答案。但他的分析表明,αs 遠非隨著距離的增加而急劇變化,而是停止增長並變為常數。
德厄爾與他的博士生導師,傑斐遜實驗室的工作人員科學家陳建平分享了這個令人震驚的發現,陳建平評論說,這個 αs 看起來像他以前見過的預測。德厄爾深入研究過去的研究,發現了其他耦合計算在長距離處變為常數的例子,很像他在資料中看到的情況。也許他有趣的 αs 計算畢竟揭示了強力的真實行為?這是一個幸運的巧合,因為儘管沒有人意識到這一點,但比約肯積分非常適合計算長距離處的 αs。雖然大多數測量探測了許多夸克之間的相互作用(因為夸克永遠不會單獨存在),但比約肯積分設法過濾掉大多數多夸克過程,並將對單個夸克的影響分離出來。事實證明,這種 αs 的計算幾乎不適用於任何其他型別的核子資料。
由於德厄爾的 αs 可能有意義,他想知道他是否可以在物理學會議上展示它,而不會有太大的被嘲笑的風險。不過,他很擔心,因為他的測量結果似乎與強力強度會持續增長的普遍智慧相矛盾。但他決定冒險。碰巧的是,布羅德斯基參加了其中一次會議,並幫助德厄爾為這項工作奠定了更堅實的理論基礎。這次會議是富有成果的合作的開始,一直持續到今天。
當德厄爾透過實驗探索 αs 時,布羅德斯基正在與蓋伊·德·特拉蒙德·佩拉爾塔和漢斯·岡特·多施合作,開發一種新的方法來計算長距離處的 QCD 性質。他們的策略使用了一種稱為全息術(通常用於研究黑洞和引力)的數學工具,透過使用在五維空間中完成的引力計算結果來推斷強力在我們四維時空(三個空間維度加上一個時間維度)中具有較大 αs 值時的行為。(這種方法所依據的額外維度是代表實際物理,還是僅僅是簡化問題的數學工具,就像經典物理學中使用虛數一樣,沒有人知道。)這種研究強力物理學的新穎方法,即所謂的輕錐全息術,可以確定長距離處的 αs,並預測將夸克和膠子限制在核子內的相互作用。
布羅德斯基長期以來一直熟悉 αs,並且知道尋找電磁力、弱力和強力統一理論的嘗試似乎要求 αs 在長距離範圍內變為有限值。事實上,他預計會出現這樣的結果,因為夸克被限制在核子內,這意味著夸克和膠子量子環不能大於質子的大小。沒有更多的環意味著耦合不再演化。因此,儘管德厄爾對 αs 的測量結果並沒有讓他感到驚訝,但他很高興看到實際上有可能測量長距離處的 αs,並且結果表明它是恆定的。
布羅德斯基和德·特拉蒙德·佩拉爾塔聯絡了德厄爾,討論如何使用他們的輕錐全息術方法計算 αs 並繼續計算。2010 年釋出的結果令人欣慰:他們的 αs 與德厄爾的實驗資料完美匹配。這尤其引人注目,因為該計算沒有任何可調引數。他們既沒有擺弄設定,也沒有亂用“湊合”因子。
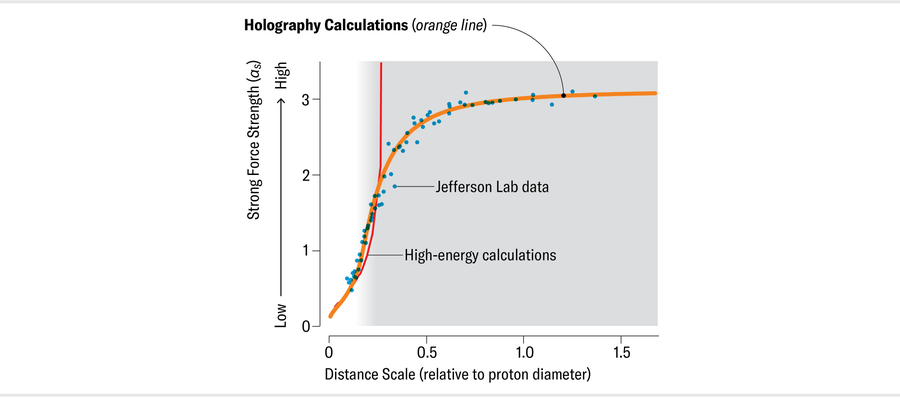
珍·克里斯蒂安森
當然,全息術是一種令人興奮的新穎方法,用於研究量子色動力學(和量子引力),但它與使用 QCD 本身不同。但我們知道,它至少很好地模擬了 QCD,這表明未來的物理學家可能能夠證明引力和強力行為之間存在某種等效性。儘管如此,為了放心地說我們真正計算了長距離處的 αs,我們需要基於 QCD 的計算。一種自然的方法是求解該理論的運動方程,QCD 中的運動方程描述了所有強力量如何隨時空變化而演化。
德厄爾在 2005 年發表了他的第一個關於 αs 的結果,幾乎是 20 年前。當時,羅伯茨對它們感到困惑,問自己,這種耦合測量,似乎專門與單個 QCD 過程相關聯,可能與該理論的運動方程有什麼關係。這樣的方程需要一個對所有過程都相同的通用耦合。他將這個問題放在一邊,然後繼續前進。
九年後,在 2014 年他與同事在義大利特倫託的歐洲核物理理論研究中心及相關領域組織的會議期間,他重新審視了德厄爾的 αs。到目前為止,理論家們已經採用了兩種平行的策略來使用 QCD 的運動方程來理解強力理論。“自上而下”的方法試圖透過膠子的性質來預測 αs。“自下而上”的方法旨在透過將預測與實驗資料進行比較,使用可直接測量的量來推斷 αs。
在 2014 年的會議上,一位傑出的同事指出,這兩種方法得出了截然不同的結果,無法調和。然而,這位同事並不知道羅伯茨與他的合作者雷·張在自下而上的方法方面取得的最新進展。在挑戰的刺激下,兩人在 24 小時內就獲得了自下而上耦合估計的結果。他們與也在會議上的自上而下領域的兩位主要參與者丹尼爾·比諾西和約阿尼斯·帕帕瓦西里烏分享了這些結果,該小組共同確定自上而下和自下而上的 αs 結果是相互相容的。平行的流合併了。
現在我們面臨一個關鍵問題:我們如何將德厄爾的耦合測量結果與我們使用 QCD 運動方程計算的值聯絡起來?如果我們能夠做到這一點,那麼我們將彌合最後的差距。
羅伯茨的下一步是與物理學家何塞·羅德里格斯-金特羅交談,他長期以來一直致力於自上而下的方法,並且可以訪問 QCD 計算機模擬的結果。在與比諾西、帕帕瓦西里烏和一位新團隊成員塞德里克·梅茲拉格進行了一些來回的頭腦風暴後,該小組得出了一個通用 QCD 耦合。令人驚訝的是,這個結果實際上與德厄爾的資料以及布羅德斯基及其同事的全息術計算無法區分。此外,與全息術結果一樣,新的預測是無引數的:沒有微調或修改。這一事實意味著該協議意義重大。
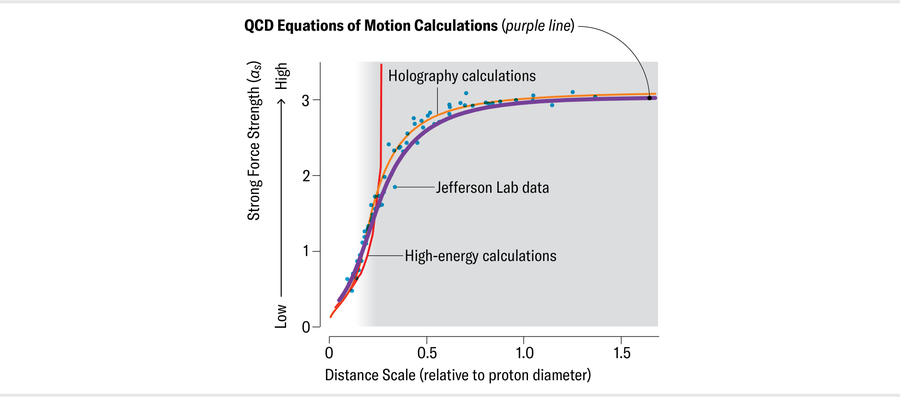
珍·克里斯蒂安森
自那時以來,利用來自自上而下、自下而上和模擬方法的改進資訊,該小組更新了其理論分析。科學家們發現,在禁地之外,他們的耦合和德厄爾的資料的吻合度優於 1%。此外,進入禁地後,他們發現夸克之間複雜的相互作用可能會破壞這些耦合之間的聯絡,但由於比約肯積分基礎過程的物理特徵,這些相互作用在很大程度上會相互抵消。這是德厄爾的幸運之處:他偶然選擇了一個過程,其耦合與從 QCD 運動方程匯出的通用結果最密切相關。
現在,我們首次擁有了涵蓋整個長度尺度範圍(包括以前無法到達的禁地)的令人信服的 αs 資料和計算。關鍵發現是,隨著距離的增加,耦合停止增長,而不變的常數再次變得恆定。這一發現具有深遠的意義。

CEBAF 大接收度譜儀進行了一些測量,這些測量有助於定義前所未有的尺度下的強力。
圖片由傑斐遜實驗室提供
首先,瞭解所有距離處的 αs 在實踐中非常重要:物理學家現在可以解析預測以前無法獲得的許多量。自然界中與強力有關的大多數現象,從我們體內原子的最深層結構到中子星的內部運作,都由 αs 的強度決定。由於這種耦合主要由其長距離行為決定,而我們現在知道它是有限的而不是無限的,因此我們開闢了一個可能的計算新世界。
在更深層次上,QCD 運動方程的解有助於揭示宇宙中 99% 可見質量的起源。這種質量來自原子,而原子的大部分質量都在其質子和中子中(電子相對較輕)。但是質子和中子的質量從何而來呢?構成它們的夸克本身也幾乎沒有質量。但在質子的尺度上,我們關於 αs 的啟示表明,夸克在其周圍聚集了膠子云,從而產生了質子的大部分質量。本質上,強力施加的強大結合能將夸克束縛在一起,幾乎貢獻了所有的質量(記住,阿爾伯特·愛因斯坦揭示能量和質量是同一枚硬幣的兩面)。因此,如果您的體重為 160 磅,那麼其中超過 158 磅來自量子色動力學,特別是由於將 αs 凍結為常數的機制。希格斯玻色子只貢獻了很小的剩餘部分——夸克和電子自身擁有的微小質量。
更重要的是,長距離處 αs 的靜態性質意味著 QCD 是第一個只預測有限量的完整量子場論。所有其他已知的量子場論,包括描述電磁力的量子電動力學,在非常高的能量下都會遇到無限的朗道極點。因此,QCD 可能會引領解釋許多超出我們當前理解範圍的現象。
沿著這條推理路線繼續下去,我們可能會了解到,例如,具有 10 個、11 個或 26 個時空維度的弦理論是否對於理解我們的宇宙是必要的,或者相反,對我們牢固建立的四個時空維度的清晰理解是否足以勝任。目前核物理學家和粒子物理學家之間的興奮是顯而易見的。