通常,每條地鐵線路在地圖上都有自己的顏色。 顯而易見的原因是,這些顏色應該儘可能地不同。 假設要修建一條新的地鐵線路。 現在,我們將解釋一種為新線路選擇一種或多種顏色的策略,使其與舊線路以及彼此之間儘可能不同。 這透過使用莫斯科地鐵地圖來說明。
•你見過綠線的新終點站嗎?"
•紅線每天早上這個時候都非常擁擠。"
•我住在橙線的盡頭,對我來說還可以:自動扶梯直接把我送到
辦公室。"
•我必須在這裡換乘紫線。 明天見!"
當然,這一切都與地鐵有關。 地下通道。 大都市地下鐵路系統。 每條線路都有自己的顏色,每種顏色都是一條線路的名稱。 當另一條線路建成時,問題就出現了:舊線路必須保持其顏色,而新線路應具有與舊線路看起來儘可能不同的顏色。 如果地鐵中有兩條或更多條新線路,情況會變得更加複雜。 新顏色不僅必須與舊顏色不同,而且它們之間也必須儘可能地不同。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
在本文中,我們將討論一種選擇這些顏色的數學策略。 順便問一下,您會為圖 1 中的真實地鐵地圖建議什麼新顏色? 出於我們的目的,這張地圖是理想的:它不僅有 14 種顏色,而且在不久的將來還將在該地鐵中修建幾條新線路(根據 [2],計劃的擴充套件線路如圖 6 所示)。 讓我們使用這張地圖來說明我們的策略——但讀者可以將這些技術應用於他或她喜歡的任何其他地圖(我們邀請讀者分析圖 2 中的倫敦地鐵地圖)。
測量顏色差異
為了最大化顏色差異——這裡是在地鐵地圖中——我們需要一種方法來測量它們並客觀地討論顏色。 為此,我們使用一些座標系(或色彩空間)將它們描述為數字元組。 例如,紅、綠、藍 (RGB) 色彩空間是眾所周知的:在其中,每種顏色都由其 RGB 分量編碼。 不幸的是,在 RGB 空間中,歐幾里得距離與人們感知到的顏色之間的可見距離不成比例。 也就是說,RGB 空間不是感知均勻的——這正是我們所期望的。
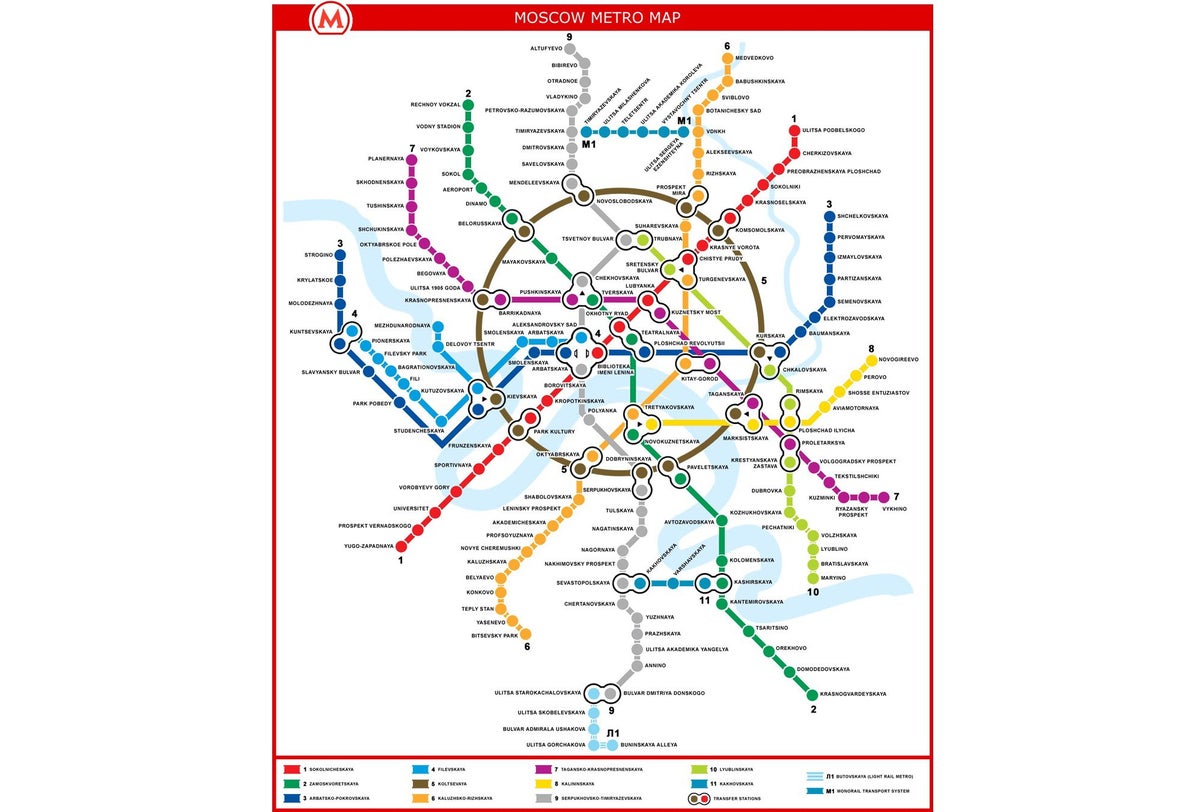
圖 1. 您很可能已經認出這裡是莫斯科地鐵。
圖片來源: 維基共享資源 (CC BY-SA 3.0)
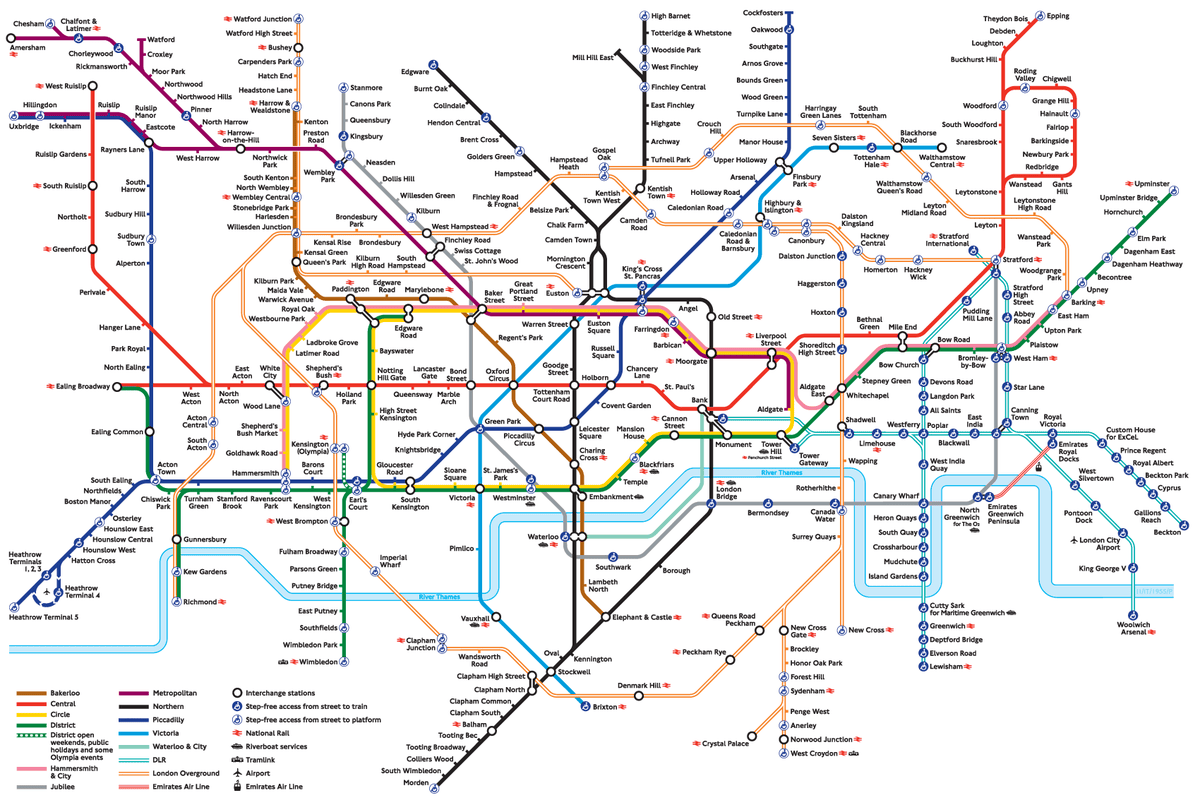
圖 2. 倫敦地鐵地圖。
圖片來源: 維基共享資源 (CC BY-SA 4.0)
1931 年,國際照明委員會 (CIE) 對數百名人類的視覺進行了測量。 根據這些資料,建立了幾個色彩空間,以使關於顏色的交流變得容易和明確。 1976 年,CIE 建議使用兩個近似感知均勻的色彩空間和色差公式。 這些空間因其官方推薦的縮寫 CIELAB 和 CIELUV 而聞名。 在前者中,顏色由三個座標描述:L(亮度)、α(紅-綠尺度)和b(黃-藍尺度)。 我們將使用這個空間用數字描述莫斯科地鐵地圖的顏色:它們的 CIELAB 座標可以在表 1 中找到;圖 3 顯示了莫斯科地鐵顏色在 CIELAB 空間中的立體圖。
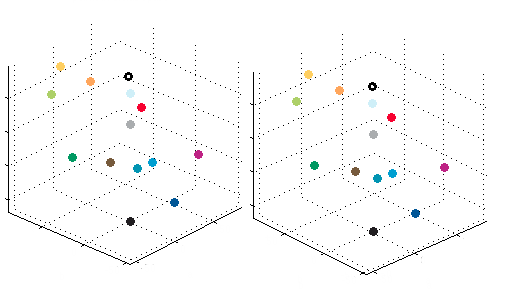
圖 3. 莫斯科地鐵地圖顏色在其在 CIELAB 空間中的位置的立體影像。 L 軸是垂直軸,a 軸從西南向東北延伸,b 軸從東南向西北延伸。 (要檢視 3 維圖片,請同時用左眼看左圖,用右眼看右圖。) 圖片來源:西蒙娜·F·格里菲恩
CIELAB 空間本身是無界的;但是,根據想要測量的內容,實際上只有一部分重要(例如,只有印表機可以列印的顏色或只有人眼可以看到的顏色)。 顏色的這種子集稱為顏色色域。 Adobe 98 的色域在 CIELAB 空間中可以在圖 4 中看到。為了使問題簡單化,我們用多面體來近似這個色域。 因為 CIELAB 空間應該幾乎是感知均勻的,所以歐幾里得距離給出了 CIE 1976 色差公式 (CIE76)
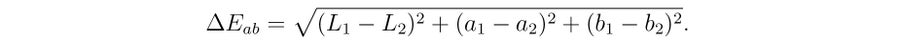
事實上,CIELAB 空間並非真正均勻。 特別是,在高 a 和 b 值下,過於簡單的 CIE76 公式與顏色感知的實驗結果相比,過分強烈地評估了色差。 這就是為什麼提出了幾個新的色差公式,其中最新的是 CIEDE2000 公式 (或 ΔΕ00)。
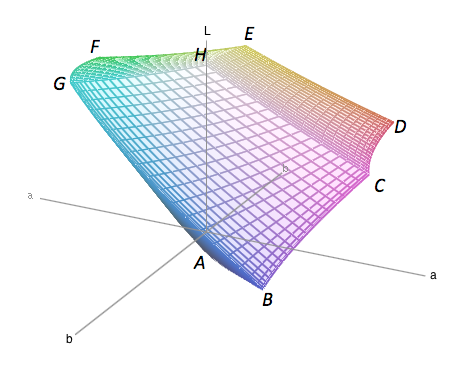
圖 4. Adobe 98 的色域在 CIELAB 空間中。 我們透過取圖中接近點 A、... H 的這個多面體的角點來近似這個色域。 圖片來源:西蒙娜·F·格里菲恩
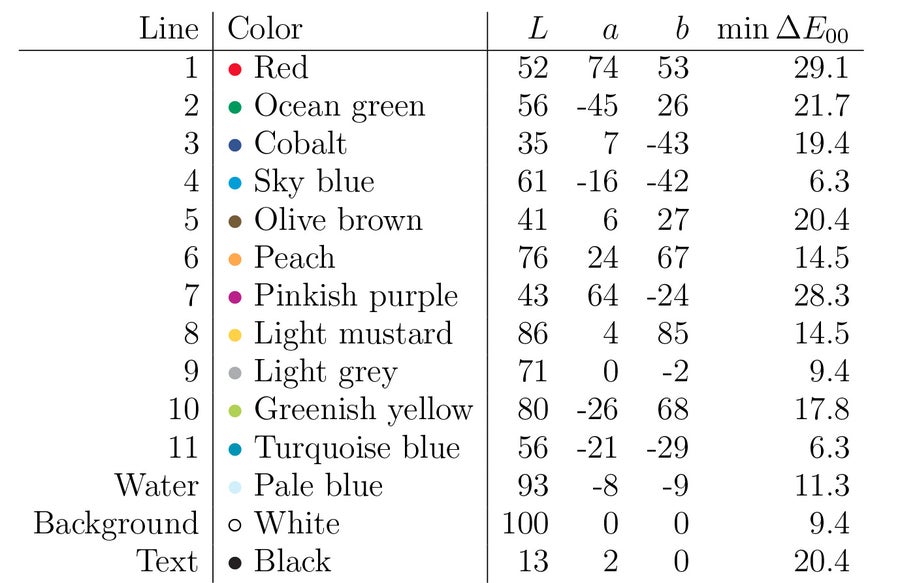
表 1. 莫斯科地鐵地圖上顏色的座標。 顏色名稱來自 [8]。 平均最小距離為 16.3。 請注意,一些最小距離是相同的;當兩個點彼此最接近時,就會發生這種情況。 圖片來源:西蒙娜·F·格里菲恩
2. 問題的數學公式
給定配備了歐幾里得度量的 CIELAB 空間——甚至更好的是,CIEDE2000 色差公式——以及顏色色域 Γ(我們選擇它是一個多面體),我們考慮一組現有的顏色 Ρ = {p1, . . . , pk} 在這個色域內,由它們的 CIELAB 座標表示(例如,參見表 1)。 如果我們只想新增一條新線路,這將導致以下極大極小問題
問題 1(一種新顏色)。 我們如何找到一個 x ∈ Γ 使得

也就是說,從新顏色 x 到現有顏色的最小距離必須儘可能大,前提是顏色 x 保持在色域 Γ 內部或邊界上。 如果我們想新增幾條新線路,每條線路都有自己的新顏色,那麼極大極小問題就變成了這樣
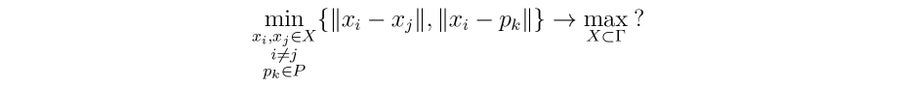
也就是說,我們最大化新顏色 x1, . . . , xm 之間的最小距離及其與舊顏色的最小距離。 或者,我們可以使用解決問題 1 的方法,逐個新增新顏色 x1, . . . , xm。 然而,這並不總是產生最佳結果。
3. 沃羅諾伊圖方法
讓我們考慮問題 1。 因為 CIELAB 空間是連續的(至少在原則上是這樣),所以不可能“嘗試色域中的所有點”來找到具有最大最小距離的點。 因此,如果只有有限數量的候選點要檢查,那將會容易得多。 這可以透過使用沃羅諾伊圖來實現。
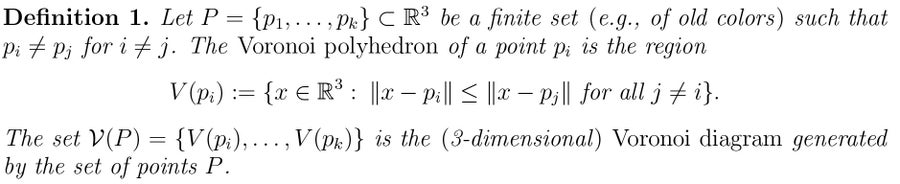
很容易證明,最大化問題 1 中最小距離的所需點 x 屬於以下各項的交集
或者:三個沃羅諾伊平面,即沃羅諾伊多面體的三個面,
或者:兩個沃羅諾伊平面和色域的邊界平面,
或者:一個沃羅諾伊平面和兩個邊界平面,
或者:三個邊界平面。
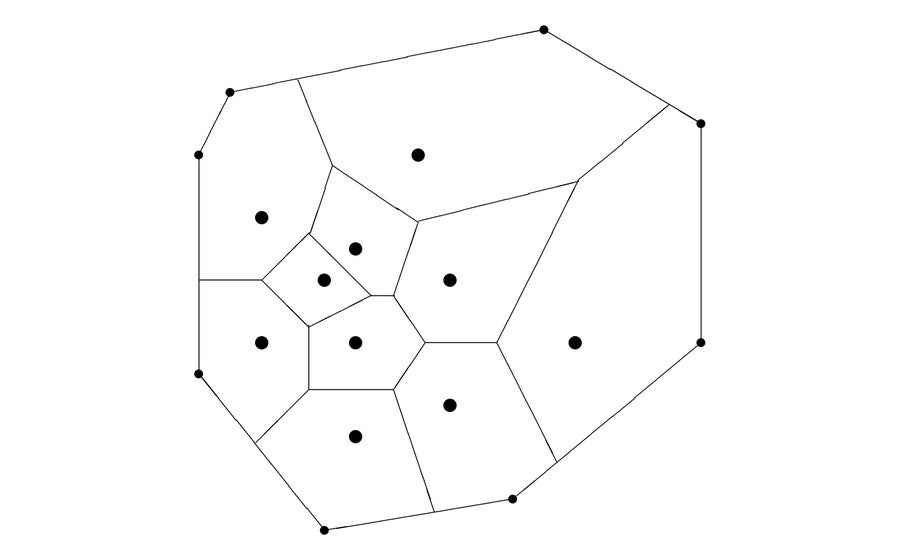
圖 5. 二維沃羅諾伊圖。 請注意,沃羅諾伊多邊形的所有邊都是連線圖中兩個點的直線的平分線的一部分。 圖片來源:西蒙娜·F·格里菲恩
這意味著,一旦計算出這些候選點,就只需比較它們到現有點 pi ∈ P 的最小距離,然後取距離最大的點即可;事實上,結果集是有限且合理小的。 這是關於歐幾里得距離的求解問題 1 的CIE76 沃羅諾伊方法。 在表 2 中,我們列出了使用此方法為莫斯科地鐵逐個獲得的五個新顏色。
很容易看出,如果存在感知均勻的色彩空間,沃羅諾伊方法將為極大極小問題 1 提供全域性最優解。 然而,如今情況並非如此,因此讓我們研究如何獲得更好的估計。
由於 CIEDE2000 距離比歐幾里得距離準確得多,我們可以透過比較 ΔΕ00 距離而不是歐幾里得距離 ΔΕαb,從候選點中選擇最佳點來改進我們的方法。 這是組合的 CIE76-CIEDE2000 沃羅諾伊方法。 當然,此方法不能單獨解決關於 ΔΕ00 的問題 1,因為候選點是透過使用 ΔΕαb 找到的。 然而,這是一種使用 CIEDE2000 距離快速獲得顏色的方法。 透過此方法為莫斯科地鐵逐個獲得的五個新顏色在表 3 中給出。 我們看到,與沃羅諾伊 CIE76 方法相比,這為我們提供了關於 CIEDE2000 距離的更好的解決方案:實際上,ΔΕ00 距離的下降速度要慢得多。
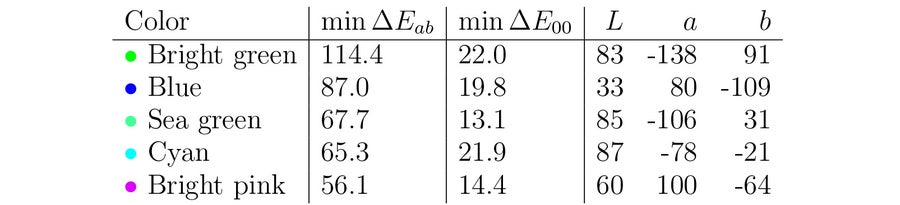
表 2. 我們使用 CIE76 沃羅諾伊方法(即,關於歐幾里得距離求解問題 1)為莫斯科地鐵的前五條新線路逐個找到的顏色。 我們在此處指示的最小距離考慮了表中較早出現的點。 請注意,最小 ΔΕ00 距離不一定在下降。 圖片來源:西蒙娜·F·格里菲恩
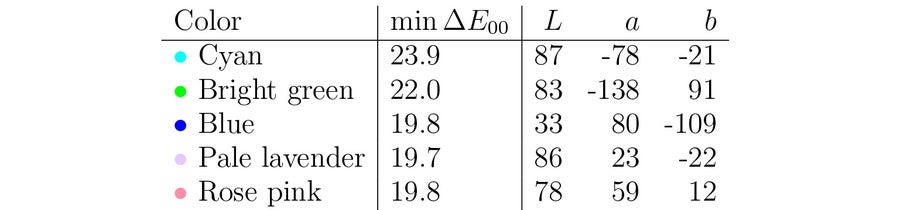
表 3. 我們使用組合的 CIE76-CIEDE2000 沃羅諾伊方法為前五條新線路逐個找到的顏色。 請注意,此處的距離是 CIEDE2000 距離,並且它們的下降速度比表 2 中慢得多。 圖片來源:西蒙娜·F·格里菲恩
4. 單純形法
我們也可以透過使用單純形法來解決關於歐幾里得距離的問題 2。 讓我們在這裡考慮顏色數量 m 為 2 的情況,這給我們提供了以下要最大化的函式,
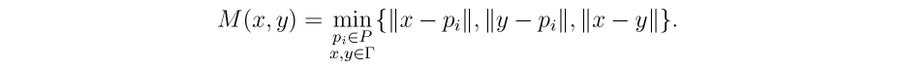
我們有 (x, y) ∈ Γ×Γ ⊂ ℝ6 。 讓我們重寫我們的問題:首先,放入一個額外的引數 x0 和兩個向量 x, y 一起放入 x = (x0, x, y) ∈ ℝ7 ,現在最大化函式 M0(x) = x0 在所有滿足約束條件 x ∈ ℝ × Γ × Γ 上
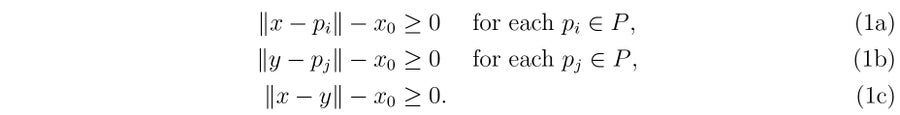
當然,使用更多關於 (x, y) 的約束來劃定集合 Γ × Γ 的範圍。 現在我們使用單純形法來最大化我們的函式。
色域的邊界給出了線性約束,非線性約束函式是方程 (1)。 因為單純形法只給我們區域性最優解,所以我們將其應用於一百萬個隨機初始點 (x0, x, y) ∈ ℝ7 (其中 x0 ∈ [0, 20] 且 (x, y) ∈ Γ × Γ)。 這些是關於 ΔΕαb 距離的區域性最優解;現在讓我們選擇具有最大 ΔΕ00 距離的解。 這樣,我們得到了兩種顏色
亮水藍色 • (84, -65, -12) 和淡粉色 • (86, 35, 7)。
它們與舊顏色和彼此之間的組合最小 CIEDE2000 距離為 22.7。 這比逐個 CIE76-CIEDE2000 沃羅諾伊方法的兩步之後獲得的最小距離要大。 因此,這為我們提供了更好的問題 2 的解決方案。 然而,這種方法非常耗時(隨著 m 的增加,單純形法將需要更多時間),因此速度快得多的沃羅諾伊方法是一個很好的替代方案。
5. 結論和討論
我們得出結論,沃羅諾伊圖方法(及其透過同時使用 CIE76 和 CIEDE2000 距離函式進行的改進)用於逐個新增新顏色,其給出的解決方案與用於一次找到兩種或更多種新顏色的非光滑最佳化方法產生的解決方案相當。 對於所研究的莫斯科地鐵地圖來說,這是正確的。 當然,其他解決方案方案也是可能的,例如蒙特卡洛方法:在色域內隨機生成新顏色 xi ∈ Γ 的測試點,而新顏色——或一組新顏色——是足夠多次此類嘗試中的極大極小最優解。 彈道方法的實現方式如下:首先,假設每個舊顏色 pi ∈ Γ 和所尋求的元組中的每個新點 xj 都帶有正電荷(因此它們會根據庫侖定律相互排斥)。 為了防止新點從色域 Γ 穿過其邊界逃逸,在邊界上最接近 xj 的點處為每個 j 放置一個可以忽略不計但為正的電荷。 透過從隨機初始資料 xj (0) ∈ Γ 開始,電荷的配置 {xj (t)} 在多面體 Γ 內部演變,根據假設,多面體 Γ 充滿了粘性介質,因此新點的運動減慢;它們遲早會在勢的區域性最小值附近被捕獲(有關這兩種方法的詳細資訊,請參見 [1])。
找到幾種新顏色仍然不是在地鐵地圖上繪製新線路所需的全部內容。 顯然,必須進一步考慮從舊線路到新線路的換乘配置——以便在新線路之間分配新顏色,從而在每個換乘站,相交線路的顏色儘可能不同。
突發新聞:線上投票。 官員表示,全長 16.8 公里、設有 8 個車站的科茹霍夫斯卡婭線計劃於 2015-2016 年出現在莫斯科地鐵系統中,參見圖 6:從海綠色開始,該線路沿著綠松石藍色延伸至紅色。
圖 6. 莫斯科地鐵的擴建計劃。
圖片來源: 維基共享資源 (CC BY-SA 3.0)
在 2014 年 10 月 20 日至 11 月 10 日舉行的互動投票中,向預先註冊的“活躍公民”提供了兩種顏色供自由選擇。 即,黑色和粉色被聲稱為色域中僅剩的尚未用於在莫斯科地鐵地圖上繪製線路的顏色(參見圖 1)。 媒體報道稱,多達 307,350 名活躍公民參加了線上投票; 71% 投票選擇粉色,18% 傾向於黑色,而 7% 信任專家(如設計師、民族學家或心理學家)的選擇。 最後,4% 的受訪者要麼提出了他們自己對新顏色的建議:綠松石色、橄欖色、珊瑚色等——甚至建議將地圖上的那條線做成斑點狀(參見 [12, 13])。
本文來自 《數學情報家》 ,經許可轉載。 它最初於 2016 年 1 月 發表。
