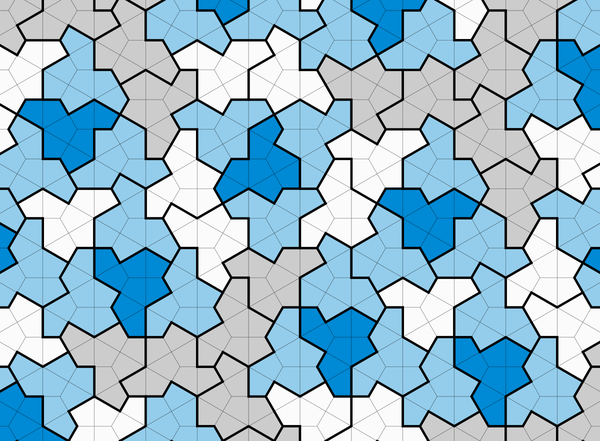
富有創意地鋪設浴室地板不僅僅是讓DIY家居裝修者感到壓力重重的任務。這也是數學中最難的問題之一。幾個世紀以來,專家們一直在研究瓷磚形狀的特殊屬性,這些形狀可以覆蓋地板、廚房防濺板或無限大的平面,而不會留下任何縫隙。具體來說,數學家們對能夠覆蓋整個平面而永不產生重複設計的瓷磚形狀感興趣。在這些特殊情況下,稱為非週期性平鋪,沒有你可以複製和貼上以保持平鋪繼續進行的模式。無論你如何切割馬賽克,每個部分都是獨一無二的。
直到現在,非週期性平鋪總是需要至少兩種不同形狀的瓷磚。許多數學家已經放棄了找到一種瓷磚解決方案的希望,這種瓷磚被稱為難以捉摸的“愛因斯坦”瓷磚,其名稱源於德語中“一塊石頭”的單詞。
然後,去年11月,英國約克郡的退休印刷系統工程師大衛·史密斯取得了一項突破。他發現了一種13邊的崎嶇形狀,他認為這可能是一種愛因斯坦瓷磚。當他告訴安大略省滑鐵盧大學的計算機科學家克雷格·卡普蘭時,卡普蘭很快意識到了這種形狀的潛力。卡普蘭與軟體開發人員約瑟夫·塞繆爾·邁爾斯和阿肯色大學的數學家海姆·古德曼-施特勞斯一起證明,史密斯的單塊瓷磚確實無縫隙且無重複地鋪滿了平面。更棒的是,他們發現史密斯不僅發現了一種,而且發現了無數種愛因斯坦瓷磚。該團隊最近在一篇論文中報告了他們的研究結果,該論文已釋出到預印本伺服器arXiv.org,尚未經過同行評審。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。
從美麗的圖案到無法證明的問題
任何走過西班牙格拉納達阿爾罕布拉宮令人歎為觀止的馬賽克走廊的人都知道平面鋪貼所涉及的藝術性。但如此美麗之中也蘊藏著無法解答的問題——正如數學家羅伯特·伯傑在1966年所說,這些問題是可證明的無法證明的。
你能否創造一個無限的馬賽克,只有相同顏色的邊緣接觸? 圖片來源:Anomie/Wikimedia
假設你想用無限數量的正方形瓷磚鋪設一個無限的表面。但是,你必須遵守一個規則:瓷磚的邊緣是彩色的,只有相同顏色的邊緣才能接觸。
有了無限的瓷磚,你開始鋪設。你找到了一種你認為會奏效的策略,但在某個時候,你遇到了死衚衕。有一個你無法用現有瓷磚填補的縫隙,你被迫將不匹配的邊緣放在一起。遊戲結束。
但當然,如果你有合適的瓷磚和正確的顏色組合,你本可以擺脫困境。例如,也許你只需要一塊所有邊緣都是相同顏色的瓷磚。數學家會檢視你的遊戲並詢問:“你是否可以透過檢視一開始給你的彩色瓷磚型別來確定你是否會遇到死衚衕? 這肯定會為你節省大量時間。”

非週期性馬賽克。 圖片來源:Claudio Rocchini/Wikimedia(CC BY-SA 3.0)
伯傑發現,答案是否定的。總會有一些情況,你無法預測是否可以在沒有縫隙的情況下覆蓋表面。罪魁禍首:非週期性平鋪的不可預測、非重複的性質。在他的工作中,伯傑發現了一組令人難以置信的20,426種不同顏色的瓷磚,它們可以鋪滿一個平面,而顏色圖案永遠不會重複自身。更棒的是,用這組瓷磚物理上不可能形成重複的圖案,無論你如何鋪設它們。
這一發現提出了另一個問題,這個問題一直困擾著數學家:共同創造非週期性鑲嵌所需的最小瓷磚形狀數量是多少?
你能降到多低?
在隨後的幾十年裡,數學家們發現了越來越小的瓷磚組合,可以創造非週期性馬賽克。首先,伯傑發現了一種包含104種不同瓷磚的組合。然後,在1968年,計算機科學家唐納德·克努特發現了一個包含92種瓷磚的例子。三年後,數學家拉斐爾·羅賓遜發現了一種只有六種瓷磚型別的變體——最後,在1974年,物理學家羅傑·彭羅斯提出了一個只有兩種瓷磚的解決方案。
.png?w=900)
著名的、優雅的彭羅斯平鋪僅使用兩種型別的瓷磚來製作非週期性圖案。 圖片來源:Inductiveload/Wikipedia
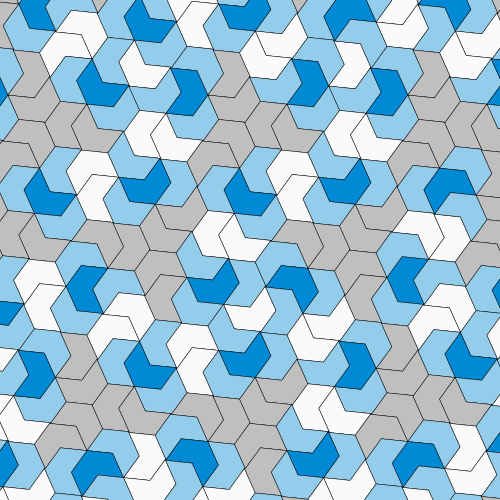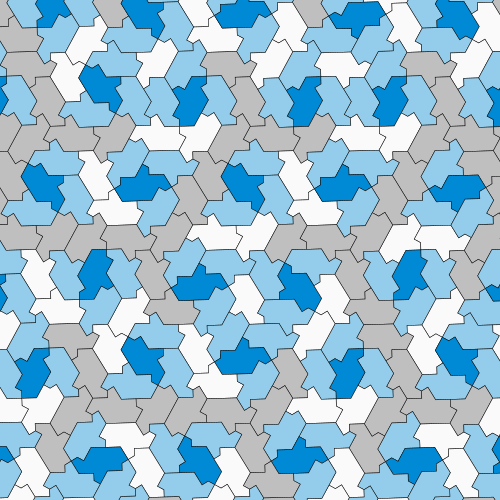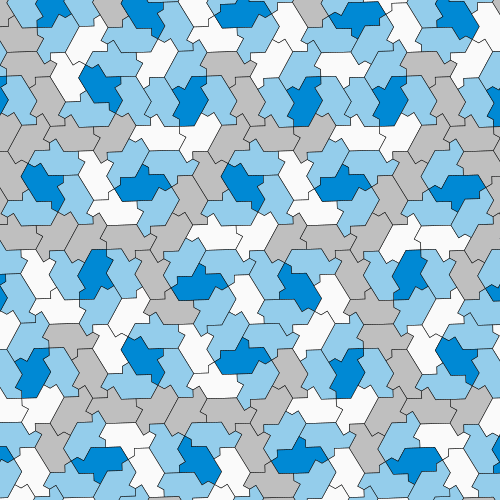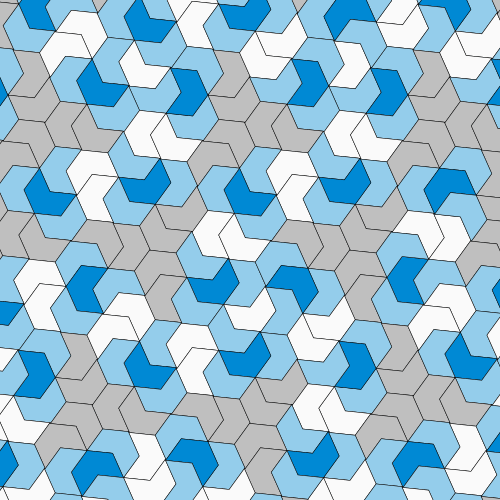
然後,進展停滯了。從那時起,許多數學家一直在尋找單塊瓷磚解決方案,即“愛因斯坦”,但沒有人成功——包括彭羅斯,他最終將注意力轉向了其他難題。但64歲的退休人員大衛·史密斯並沒有放棄。據《紐約時報》報道,他喜歡玩PolyForm Puzzle Solver,這是一款讓使用者設計和組裝瓷磚的軟體。如果一個形狀看起來很有希望,史密斯會剪出幾張紙質拼圖來嘗試。然後,在2022年11月,他偶然發現了現在著名的瓷磚,他稱之為“帽子”,因為它像頂帽子——儘管卡普蘭強調許多人認為它更像一件T恤。
_webp.jpeg?w=292)
史密斯的13邊瓷磚看起來像帽子或T恤,具體取決於你的看法。 圖片來源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
當卡普蘭收到史密斯發來的帶有“帽子”的電子郵件時,他很快就對此產生了興趣。在軟體的幫助下,他排列了越來越多的帽子形瓷磚,看起來它們似乎真的可以覆蓋平面而不會形成重複的圖案。
但是,如果他繼續鋪設瓷磚,這種重複的圖案仍然可能會顯現出來——也許只有當平面長達數光年時,才會出現冗餘部分。研究人員需要從數學上證明這種平鋪是非週期性的。卡普蘭轉向了邁爾斯和古德曼-施特勞斯,他們過去在平鋪方面做了大量工作。
起初,他們對潛在的愛因斯坦瓷磚的簡單性感到驚訝,因為“帽子”具有相當簡單的13邊形狀。如果你之前問過古德曼-施特勞斯,難以捉摸的愛因斯坦瓷磚會是什麼樣子,“我會畫一些瘋狂的、彎曲的、令人討厭的東西,”他告訴《科學新聞》。隨著數學家們仔細觀察這個形狀,他們意識到他們可以調整邊的長度,仍然可以創造出無縫的非週期性馬賽克。這種形狀打開了通往無數種愛因斯坦瓷磚的大門。
永不重複的圖案
數學家需要確鑿的證據來支援他們的主張。首先,他們使用了專家們幾十年來一直依賴的方法來證明某些型別的瓷磚可以創造非週期性馬賽克。但邁爾斯也超越了這些舊方法,創造了一種全新的證明方法,這種方法也可能對其他平鋪有用。
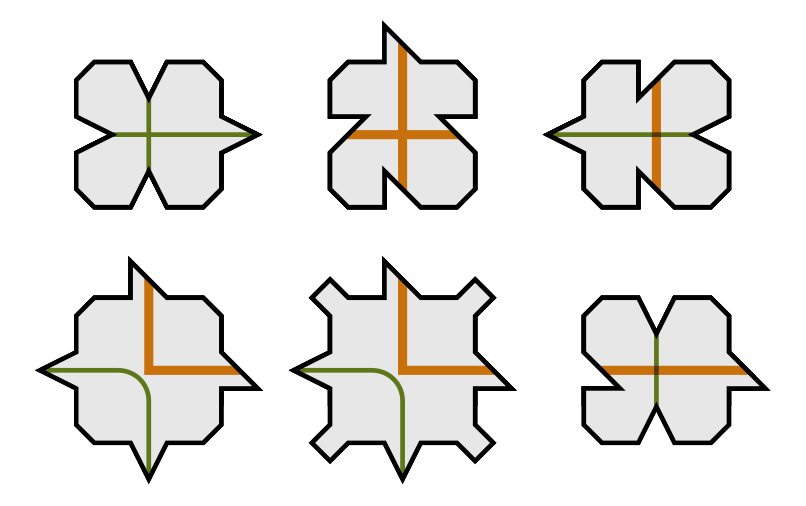
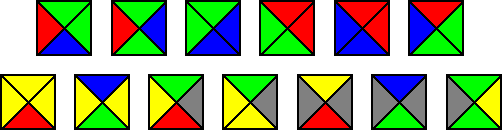
羅賓遜的六片瓷磚組合。 圖片來源:Archibald/Wikimedia
使用羅賓遜1971年的六片瓷磚組合可以最好地解釋經過驗證的可靠方法。羅賓遜瓷磚上繪製的橙色和綠色線條的作用類似於先前無限正方形示例中的彩色邊緣。這裡的規則同樣簡單:只有當綠色和橙色線條平滑地延續時,才能將兩片羅賓遜瓷磚彼此相鄰放置。
遵循此規則會產生一個可識別的圖案,該圖案由越來越大的橙色正方形組成。如果你不斷縮小,正方形會繼續變大並相互交叉。這建立了一個層次結構,其中馬賽克的每個部分都有其獨特的位置。你不能在不違反規則和破壞結構的情況下移動或交換任何部分。這告訴我們,鑲嵌必須是非週期性的。

羅賓遜平鋪形成互鎖的、分層的橙色正方形。 圖片來源:C G Strauss/Wikimedia
卡普蘭、古德曼-施特勞斯和邁爾斯能夠證明史密斯提出的帽子形愛因斯坦瓷磚也具有類似之處。為了使瓷磚更易於使用,他們將帽子的崎嶇邊緣平滑成更易識別和有用的形狀——例如,單片帽子瓷磚可以用三角形近似。他們還使用多塊愛因斯坦瓷磚的簇來建立不同的形狀。他們可以將四片帽子瓷磚排列成類似六邊形的結構,兩片瓷磚排列成五邊形,另外兩片瓷磚組合排列成平行四邊形。然後,這四種平滑後的形狀(每種形狀都僅由愛因斯坦瓷磚組成)可以完全覆蓋平面,形成圖案。
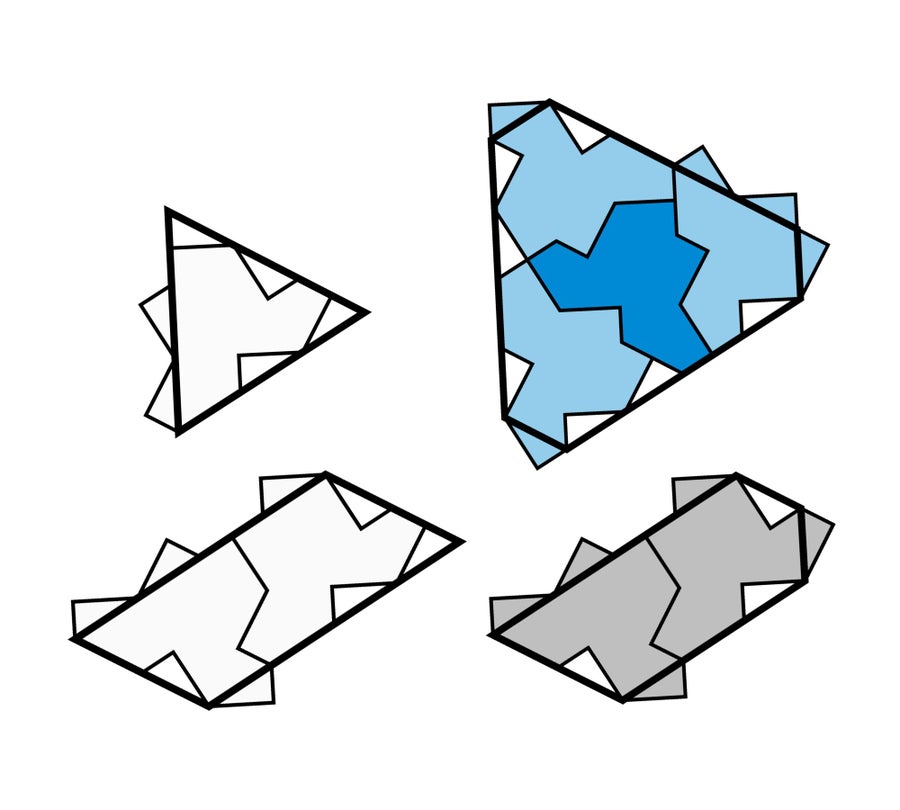
帽子形瓷磚可以組合成更大、更平滑的多邊形,以證明瓷磚形狀的非週期性。 圖片來源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
數學家證明,這種平鋪不包含重複的圖案,因為就像羅賓遜的六片瓷磚組合一樣,這四種特殊形狀形成了層次結構。如果你將這四種愛因斯坦瓷磚簇(六邊形、五邊形、平行四邊形和三角形)組合在一起,它們將不可避免地建立一個更大的版本,版本形狀與其中一個相同的形狀。然後,如果你將這些更大的形狀組合在一起,你將建立更大版本的這些形狀,依此類推。這個過程可以無限重複,從而產生層次結構。因此,整體圖案無法分割成重複的部分。如果你只是將圖案的部分滑動到另一個位置,那麼總體結構將被破壞。
%5B2%5D_webp.jpeg?w=900)
愛因斯坦瓷磚的多邊形簇形成分層的非週期性結構。 圖片來源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
兩種證明勝過一種
這個證明需要進行一些複雜的計算,因此這三位科學家尋求了計算機的幫助。他們免費釋出了他們的計算機輔助證明,以便任何人都可以檢查是否有錯誤。
但邁爾斯仍然不滿意。他建立了一種新的證明非週期性的方法,這種方法可以透過手工完成,無需計算機,透過表明愛因斯坦帽子與更容易研究的其他著名平鋪有關。這些相關的平鋪由稱為多邊形鑽石的形狀製成,多邊形鑽石是由組合等邊三角形形成的簡單瓷磚。邁爾斯調整了一些愛因斯坦帽子的邊緣,形成了兩種不同的多邊形鑽石排列,它們遵循帽子相同的平鋪圖案——一種形狀像人字形,另一種形狀像六邊形和菱形組合在一起。儘管它們的視覺差異,但這三種排列都具有相同的屬性。如果數學家能夠證明這兩種多邊形鑽石平鋪都是非週期性的,那麼原始平鋪也必須是非週期性的。
數學家可以透過將愛因斯坦瓷磚調整為兩種更易於研究的形狀來探測其屬性。 圖片來源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
值得慶幸的是,對於多邊形鑽石,該證明只是基本的數學問題。數學家可以用一個稱為平移向量的量來表示多邊形鑽石排列的對稱性。如果這兩個新排列包含重複的圖案,則其平移向量的長度應該彼此相關——具體而言,它們的比率應該是有理數。但相反,向量的比率為根號2——絕對是一個無理數——表明多邊形鑽石排列不是週期性的。因此,最初的帽子瓷磚確實是愛因斯坦瓷磚。
科學家們在他們的論文中解釋說,邁爾斯的新證明方法也可能對其他平鋪有所幫助。但就目前而言,專家和業餘平鋪愛好者都對擁有期待已久的愛因斯坦瓷磚感到興奮。家居裝飾的可能性真的是無限的。正如威廉姆斯學院的數學家科林·亞當斯告訴《新科學家》,“如果我現在要鋪設浴室,我會把它放在我的浴室裡。”
本文最初發表於《Spektrum der Wissenschaft》,並經許可轉載。
編者注(8/2/23):本文在釋出後進行了編輯,以更正拉斐爾·羅賓遜的名字和他的六片瓷磚組合的推出年份。