大多數人很少處理無理數——這樣做是不理智的,因為它們會永遠延續下去,並且準確地表示它們需要無限的空間。但是,諸如 π 和 √2 等無理常數(無法簡化為簡單分數的數字)經常出現在科學和工程領域。自古希臘以來,這些難以處理的數字一直困擾著數學家;事實上,傳說希帕索斯因提出無理數的存在而被淹死。然而,現在,一個關於無理數可以被多好地近似的、近 80 年的難題已被解決。
許多人透過將無理數四捨五入為分數或小數來概念化它們:將 π 估計為 3.14,相當於 157/50,這導致了 3 月 14 日 Pi 節的廣泛慶祝。然而,另一種近似值 22/7 更容易處理,也更接近 π。這就引出了一個問題:這些近似值的簡單性和準確性是否會受到限制?我們是否可以以我們想要的任何形式選擇分數?
1941 年,物理學家理查德·達芬和數學家阿爾伯特·謝弗提出了一個簡單的規則來回答這些問題。考慮一個近似各種無理數的任務。首先,確定對於特定分母的分數,近似值應該有多接近。(記住,“分子”指的是分數的頂部,“分母”指的是底部。這裡,所有的分數都已完全簡化——例如,2/4 不算作分母為 4,因為它簡化為 1/2。)你可能會決定,形式為 n/2 的簡化分數可以近似任何無理數,其真值落在它們的 1/10 範圍內——給近似值一個 1/10 的“誤差”。分母為 10 的分數 n/10 在數軸上比分母為 2 的分數更接近,因此在這種情況下,你可能會將誤差限制為僅 1/100——這些分數可以近似它們 1/100th 範圍內的任何值。
支援科學新聞事業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和想法的具有影響力的故事的未來。
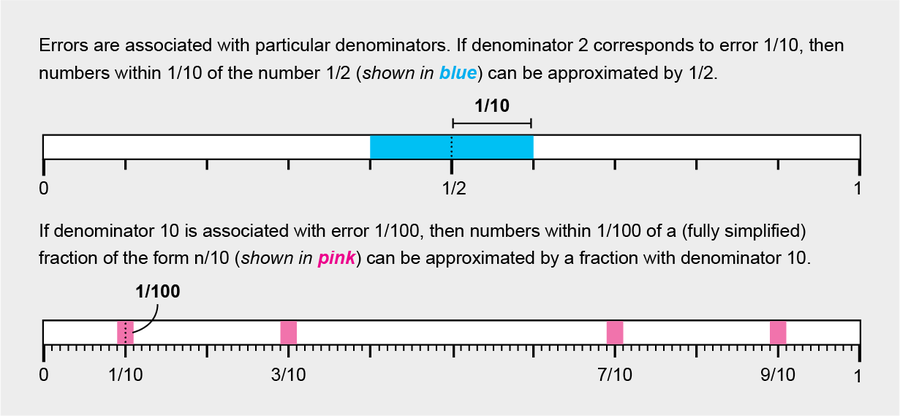
圖片來源:Amanda Montañez
通常,較大的分母與較小的誤差相關聯。如果這是真的,並且有無限多的分母可以用來將一個數字近似到相應的誤差範圍內,那麼透過增加分母,可以使近似值越來越好。達芬和謝弗的規則衡量了何時可以根據誤差的大小來做到這一點。
如果選擇的誤差在總體上足夠小,那麼隨機選擇的無理數 x 將只有有限數量的良好近似值:它可能落在具有特定分母的近似值之間的間隙中。但是,如果誤差足夠大,那麼將有無限多的分母可以建立一個良好的近似分數。在這種情況下,如果誤差也隨著分母的增大而縮小,那麼您可以選擇您想要的任何精度的近似值。
未證明
結論是,要麼你可以任意好地近似幾乎每個數字,要麼幾乎沒有一個數字可以做到。蒙特利爾大學的數學家迪米特里斯·庫庫洛普洛斯說:“存在著鮮明的二分法。” 此外,您可以隨意選擇誤差,只要它們在總體上足夠大,大多數數字就可以透過無限多種方式近似。這意味著,透過將一些誤差選擇為零,您可以將近似值限制為特定型別的分數——例如,僅限分母為 10 的冪的分數。
儘管小誤差似乎使近似數字變得更加困難,但達芬和謝弗無法證明他們的猜想——其他人也無法證明。奧地利格拉茨科技大學的數學家克里斯托夫·艾斯萊特納說,該證明仍然是數論中的“里程碑式的未解決問題”,他研究過這個問題。直到今年夏天,庫庫洛普洛斯和他的合著者詹姆斯·梅納德在釋出到預印本伺服器 arXiv.org 的論文中宣佈了他們的解決方案。
達芬-謝弗猜想“在通常異常困難和複雜的數學領域中具有這種神奇的簡單性,”牛津大學教授梅納德說。他是偶然發現這個問題的——他是一位數論學家,但與大多數達芬-謝弗專家不在同一領域。(他通常研究素數——那些只能被自身和 1 整除的數。)約克大學的一位教授在梅納德在那裡的一次演講後建議他解決達芬-謝弗猜想。“我認為他有一種直覺,即讓稍微局外的人來做這件事可能會有好處,”梅納德說。事實證明這種直覺是正確的,儘管它在幾年後才結出果實。在最初的對話很久之後,梅納德向庫庫洛普洛斯建議合作,因為他懷疑他的同事具有相關的專業知識。
梅納德和庫庫洛普洛斯知道,該領域以前的工作已將問題簡化為關於分母的素因數的問題——素因數是相乘在一起產生分母的素數。梅納德建議將這個問題視為數字著色:“想象一下,在數軸上,將所有接近分母為 100 的分數的數字著色。” 達芬-謝弗猜想說,如果誤差足夠大,並且對每個可能的分母都這樣做,那麼幾乎每個數字都將被無限多次著色。
對於任何特定的分母,只有部分數軸會被著色。如果數學家能夠證明對於每個分母,著色的區域都足夠不同,他們就可以確保幾乎每個數字都被著色。如果他們還能證明這些區域是重疊的,他們就可以得出結論,這種情況發生了很多次。捕捉不同但重疊區域這一思想的一種方法是證明由不同分母著色的區域彼此無關——它們是獨立的。
但這實際上並非如此,特別是當兩個分母共享許多素因數時。例如,可能的分母 10 和 100 共享因數 2 和 5——並且可以被 n/10 形式的分數近似的數字與可以被 n/100 形式的分數近似的數字表現出令人沮喪的重疊。
繪製問題圖
梅納德和庫庫洛普洛斯透過將問題重新定義為數學家稱為圖的網路來解決這個難題——一組點,其中一些點透過線(稱為邊)連線。他們圖中的點代表研究人員想要用於近似分數的可能分母,如果兩個點有許多共同的素因數,則它們之間透過邊連線。在允許的分母具有不需要的依賴性的情況下,這些圖恰好有很多邊。
使用圖使兩位數學家能夠以新的方式視覺化問題。“你需要獲得的最大見解之一是忘記問題的所有不重要部分,而只專注於使 [它] 非常特殊的一個或兩個因素,”梅納德說。他說,使用圖,“不僅可以讓你證明結果,而且它真正告訴你一些關於問題中正在發生的結構性事情。” 梅納德和庫庫洛普洛斯推斷,具有許多邊的圖對應於一種特定的、高度結構化的數學情況,他們可以單獨分析這種情況。
這對組合的解決方案讓該領域的許多人感到驚訝。“普遍的感覺是這個問題離解決還很遠,”艾斯萊特納說。“使用 [圖] 的技術是未來可能會被認為與——甚至可能比——實際的達芬-謝弗猜想更重要的東西,”德克薩斯大學奧斯汀分校的退休教授傑弗裡·瓦勒說,他於 1978 年證明了該猜想的一個特例。
其他專家可能需要幾個月的時間才能理解全部細節。“現在的證明是一個漫長而複雜的證明,”艾斯萊特納說。“僅僅有一個引人注目的、輝煌的想法是不夠的。有很多很多部分需要控制。” 這篇長達 44 頁的密集技術數學論文,即使是頂級的數學頭腦也需要時間來理解。然而,社群似乎很樂觀。瓦勒說:“這是一篇很棒的論文。我認為它是正確的。”