你可能會驚訝地發現,你無法在不產生旋毛的情況下將椰子上的毛髮梳平。 也許更令人驚訝的是,這個看似荒謬的主張,以及更滑稽的名字“毛球定理”,是數學分支——拓撲學中的一項重要發現。 拋開略顯幼稚的幽默感不談,這個定理在氣象學、無線電傳輸和核能領域都有著深遠的影響。
在這裡,“旋毛”可以指禿斑,也可以指像《小搗蛋》角色阿爾法法頭上的那種直立的綹。 當然,數學家在構建問題時不會提到椰子或旋毛。 用更專業的術語來說,可以將椰子想象成一個球體,而毛髮則視為向量。 向量通常用箭頭表示,它只是具有大小(或長度)和方向的東西。 將毛髮貼著椰子表面梳平,就相當於形成切向量——即沿著其長度僅在一個點與球體相切的向量。 此外,我們想要一把光滑的梳子,因此不允許在任何地方分縫。 換句話說,球體上的向量排列必須是連續的,這意味著附近的毛髮方向應該僅逐漸變化,而不是劇烈變化。 如果我們將這些標準結合在一起,該定理指出,無論你如何嘗試將向量分配給球體上的每個點,都必然會發生一些“醜陋”的事情:會出現不連續性(分縫)、長度為零的向量(禿斑)或未能與球體相切的向量(阿爾法法)。 用完整的術語來說:球體上連續的非零切向量場是不可能存在的。
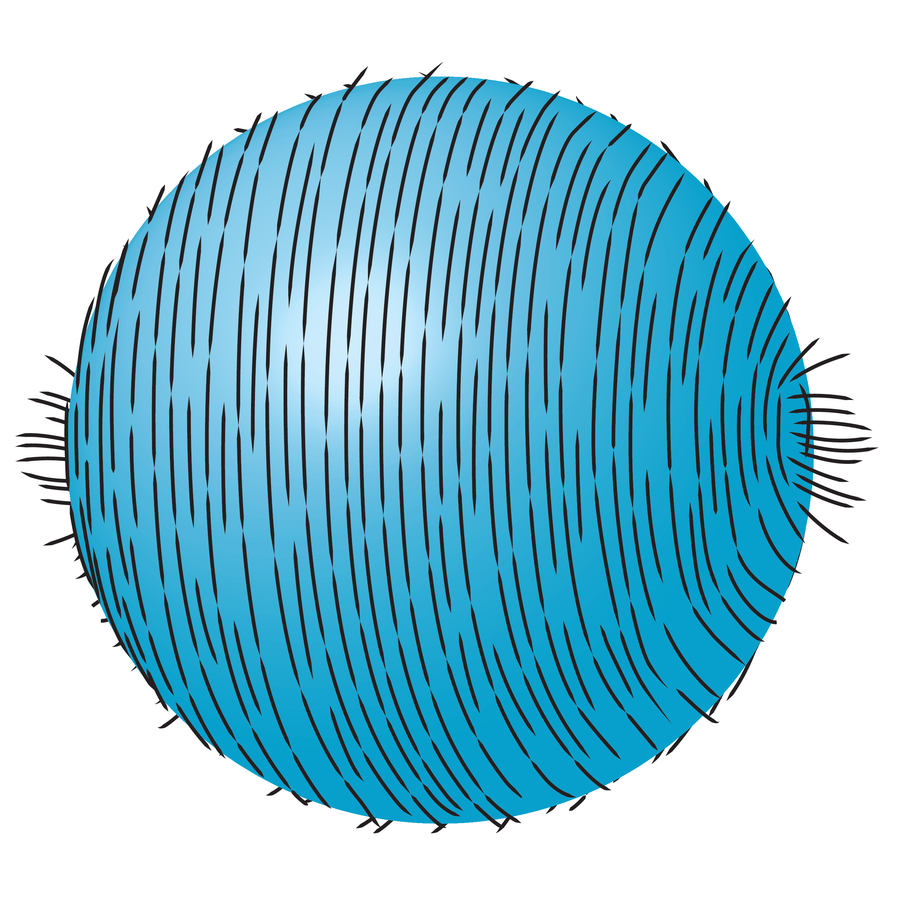
這個球體上佈滿了類似毛髮的小線條,它們都朝同一方向梳理。兩側的簇狀物演示了毛球定理。 圖片來源:Buckyball Design
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。 透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的、具有影響力的故事。
這一論斷適用於各種毛茸茸的物體。 在拓撲學領域,數學家研究形狀,就像在幾何學中一樣,但他們想象這些形狀是由一種永恆的彈性橡膠製成的。 雖然這種橡膠能夠塑造成其他形狀,但它無法撕裂、融合或穿過自身。 如果一個形狀可以平滑地變形為另一個形狀而不做這些事情,那麼對於拓撲學家而言,這些形狀是等價的。 這意味著毛球定理自動適用於毛茸茸的立方體、毛茸茸的填充動物和毛茸茸的棒球棒,它們在拓撲學上都等價於球體。(你可以用一塊橡皮泥將它們都捏出來,而不會違反橡膠規則。)
與球體不等價的東西是你的頭皮。 頭皮本身可以展平成一個表面,並像長毛地毯上的纖維一樣朝一個方向梳理。 所以遺憾的是,數學不能為你的起床頭開脫。 甜甜圈也與球體不同,因此一個毛茸茸的甜甜圈——毫無疑問,這是一個令人倒胃口的形象——可以被順利地梳理平整。

這個甜甜圈形狀上佈滿了類似毛髮的小線條,它們都朝同一方向梳理,沒有形成簇狀物。 圖片來源:Buckyball Design
這是毛球定理一個有趣的推論:地球上總會至少有一個點,那裡的風不會沿著表面吹動。 風在全球範圍內持續迴圈流動,其在地球表面每個位置的方向和大小都可以用與地球相切的向量來模擬。(向量的大小不需要表示物理長度,例如毛髮的長度。) 這符合定理的前提,這意味著風必須在某處停止(形成旋毛)。 旋毛可能出現在氣旋的中心或漩渦,或者可能是因為風直接向上吹向天空。 這個簡潔的線上工具描繪了地球上最新的風流,你可以清楚地看到那些漩渦狀的旋毛。
為了觀察該定理的另一個奇特推論,可以隨意旋轉籃球。 球的表面上總會有一個點的速度為零。 同樣,我們基於球上每個點的方向和速度,將一個切向量與該點關聯起來。 旋轉是一個連續的運動,因此毛球定理適用,並保證存在一個速度為零的點。 經過進一步思考,這似乎是顯而易見的。 旋轉的球體圍繞著一條看不見的軸旋轉,而該軸兩端的點不會移動。 如果我們沿著該軸在球上鑽一個小孔,以移除靜止的點會怎樣? 這樣一來,似乎每個點都會移動。 這是否違反了毛球定理? 不,因為鑽孔將球體變成了甜甜圈! 即使是孔異常細長的甜甜圈,也無視該定理的規則——矛盾得以避免。
從玩具場景轉向實際應用——毛球定理實際上對無線電工程師施加了實際的限制。 天線根據設計選擇在不同的方向上廣播無線電波。 有些天線將其訊號朝特定方向發射訊號,而另一些天線則更廣泛地輻射訊號。 人們可能會傾向於簡化問題,只製造在每個方向上同時傳送等強度訊號的天線,這些天線被稱為各向同性天線。 但只有一個問題:拓撲學中的一個“毛茸茸”的事實表明,各向同性天線是不可能存在的。 想象一下從中心源發出的波球。 在離源足夠遠的地方,無線電波會表現出垂直於其傳播方向的電場,這意味著該電場與波球相切。 毛球定理堅持認為,該電場必須在某處降至零,這意味著天線訊號中存在干擾。 各向同性天線僅僅作為理論理想存在,我們用它來比較實際天線的效能。 有趣的是,聲音傳播的是另一種波,它不具有無線電波的垂直特性,因此可以製造出在每個方向上發出等強度聲音的揚聲器。
也許毛球定理最酷的應用與核聚變能有關。 核聚變能承載著巨大的希望——也許在未來的某一天——能夠幫助緩解能源危機。 它有潛力產生大量的能量,而不會帶來困擾化石燃料的環境問題,並且與傳統的核裂變反應堆相比,放射性風險也大大降低。 簡而言之,聚變反應堆首先使用氫等燃料,並將其置於高溫高壓下,這會將其分解成組成部分,形成等離子體。 等離子體是電子和其他帶電粒子的雲團,它們四處移動,偶爾融合在一起形成新的粒子,並在該過程中釋放能量。
在建造聚變反應堆時,存在一個基本的工程障礙:如何容納比太陽核心熱 10 倍的等離子體? 沒有任何材料能夠承受如此高的溫度而不分解成等離子體本身。 因此,科學家們設計了一個巧妙的解決方案:他們利用等離子體的磁性將其限制在強磁場中。 最自然的容器設計(想想盒子或罐子)在拓撲學上都等價於球體。 圍繞任何這些結構的磁場都會形成連續的切向量場,而在這一點上,我們知道這種“毛茸茸”的結構會發生什麼。 磁場中的零點意味著容器洩漏,這對整個反應堆來說是災難性的。 這就是為什麼領先的聚變反應堆設計——託卡馬克裝置——具有甜甜圈形狀的腔室的原因。 國際熱核聚變實驗反應堆 (ITER) 大型專案計劃在 2025 年前完成在法國建造新的託卡馬克裝置,相關人員聲稱他們的磁約束系統將是“有史以來建造的規模最大、整合度最高的超導磁體系統”。 這就是拓撲學在我們清潔能源未來中發揮的作用。
這是一篇觀點和分析文章,作者或作者表達的觀點不一定代表《大眾科學》的觀點。
