數學家在更高維度中重新發明輪子，解決數十年之久的幾何難題

數學家們正在“重新發明輪子”，透過賦予它一種新的形狀。他們新構想的輪子看起來像一個多維度的撥片，並且理論上可以以超出我們三維理解的方式滾動。這項突破透過展示如何在無法想象的維度中構建物體，解決了數十年之久的幾何難題。

“這是一個令人驚歎的理論，”以色列愛因斯坦數學研究所的教授 Gil Kalai 說，他沒有參與這項研究。結果證明，這些難以理解的物體可以在任何維度中構建，其尺寸僅為圓形或球體等更傳統的滾動形狀的一小部分。

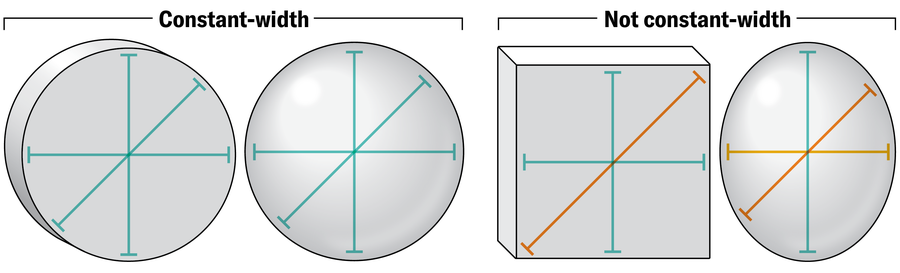
輪子之所以能滾動，是因為它們是具有“恆定寬度”的物體——從每個角度看，它們的寬度都相同。這種幾何屬性使輪子在移動時能夠在兩個平行平面（例如地面和汽車）之間保持恆定的距離。本質上，如果一個形狀可以平穩滾動而不會晃動，那麼它就具有恆定寬度。例如，將一個網球放在你平行的雙手之間並旋轉它——你會看到你的手永遠不會更靠近或更遠離，因為球具有恆定寬度的幾何形狀。像雞蛋這樣的橢圓形形狀將無法透過該測試。

支援科學新聞報道

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱，您正在幫助確保未來能夠繼續報道關於塑造我們當今世界的發現和思想的具有影響力的故事。

圓形和球體是恆定寬度形狀的簡單、直觀的例子，人類已經使用它們來促進運動數千年。這些是特殊型別的恆定寬度形狀，稱為“球體”——所有邊界點與中心距離相同的形狀。在二維中是圓形，在三維中是球體，並且這個概念延伸到我們無法輕易視覺化的更高維度。

由於邊界點都位於距中心點固定距離的位置，因此這些球體體積龐大：它們在任何維度中都具有恆定寬度形狀的最大可能體積。但是，體積如此龐大並不總是理想的。在 20 世紀 80 年代，數學家 Oded Schramm 提出了一個問題：我們如何在任何維度中找到具有最小體積的恆定寬度形狀？Kalai 說，這“是一個非常基本的問題”，數學家們一直有興趣解決這個問題。“但沒有人有任何探測它的方法。”

這個問題一直存在到今年 6 月，當時一個國際數學家團隊提出了一種構建恆定寬度形狀的新方法。研究人員的方法涉及無限數量的n維球體的交集，並在預印本伺服器 arXiv.org 上以簡潔的三頁證明形式釋出。“配方本身非常簡單，”挪威科技大學數學教授、研究合著者 Andriy Bondarenko 說。雖然使用和分析這個配方相對簡單，但研究人員花了數年時間才“[理解]為什麼我們首先應該考慮這個配方。”

平面國裡的輪子

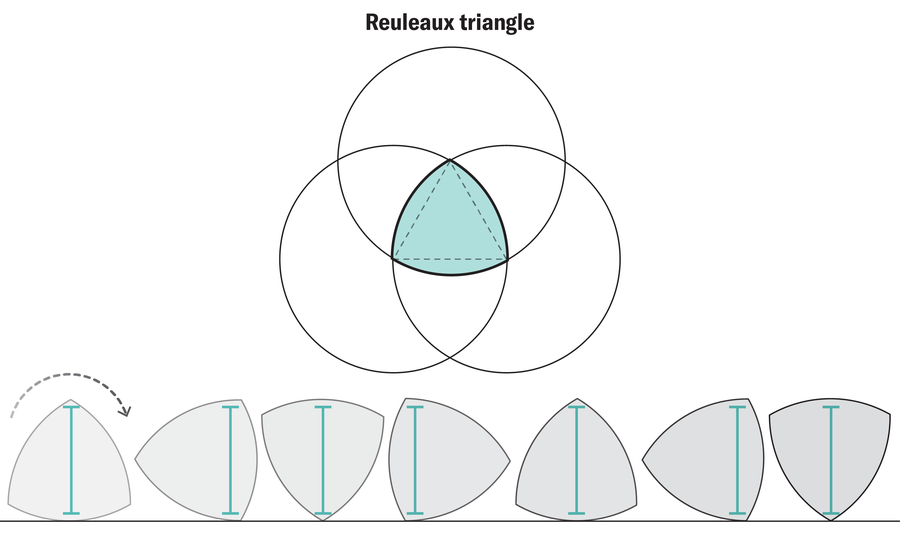
這項最新的工作率先研究了任何維度中的恆定寬度形狀，但是在二維或三維中設計輪子本身並不是一個新問題。對於這些容易理解的較低維度，數學家們已經發現了許多體積更小的恆定寬度形狀。在二維中，勒洛三角形具有恆定寬度形狀的最小面積。您可以使用一種三向維恩圖自行繪製此形狀。首先，繪製一個等邊三角形，然後在每個角周圍新增三個半徑相等的圓。在這些圓的中心，您會發現一個圓角形狀，它像一個圓一樣滾動，但尺寸只有圓形的一小部分。

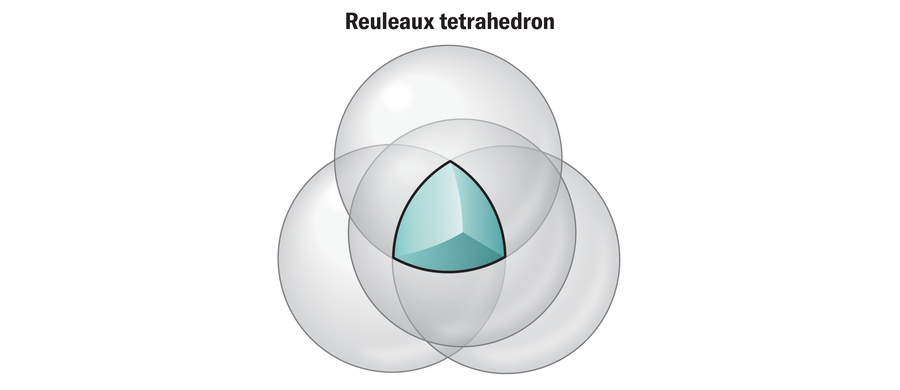
在三維中，您可以使用類似的方法：從正四面體（一種由四個等邊三角形組成的形狀）開始，並在其每個頂點新增一個球體。這些重疊球體中心形成的形狀稱為勒洛四面體。它並非完全恆定寬度——它很接近，但邊緣伸出太多。但是，稍微打磨一下，就會產生恆定寬度的形狀。這可以透過兩種不同的方式完成，以形成兩種略有不同的形狀，稱為邁斯納體。

但是，這些形狀背後的簡單公式無法提供關於如何在四維或更高維度中構建的見解，這超出了人類的感知範圍。“推廣勒洛結構非常困難，”Bondarenko 說。“如果這很容易，以前就有人做過了。”

更高維度中的輪子

最新的工作透過擴充套件勒洛交集方法，提供了一種在任何維度中構建恆定寬度物體的通用演算法。數學家團隊使用了一種相關的類似維恩圖的方法來產生所需的新形狀——一個位於更高維度空間中心的幾何異常小塊。

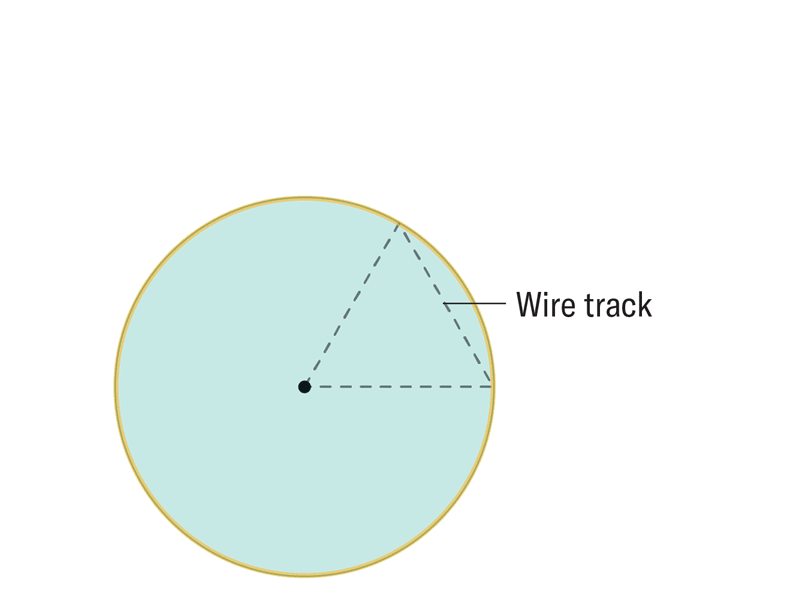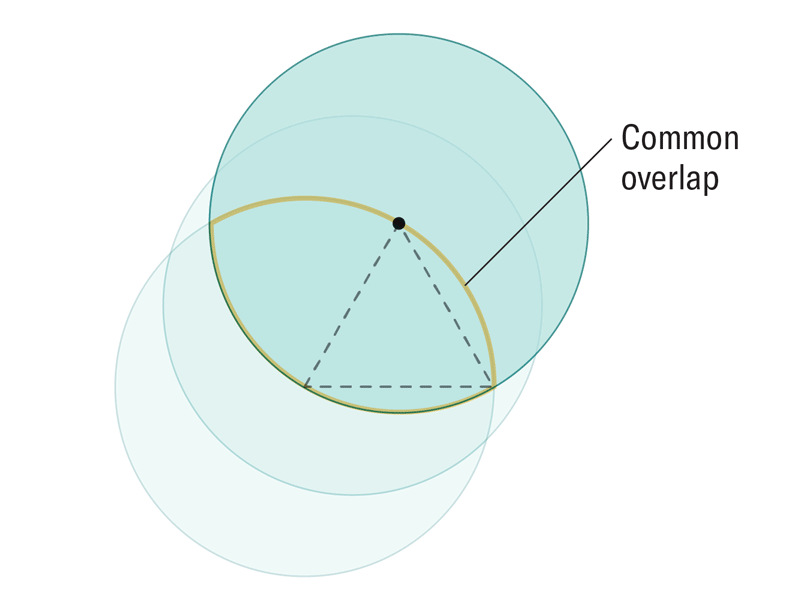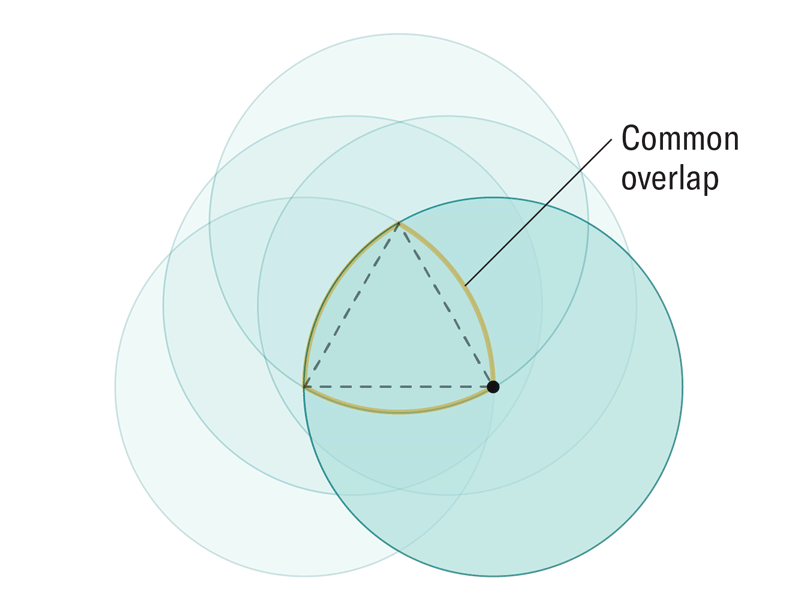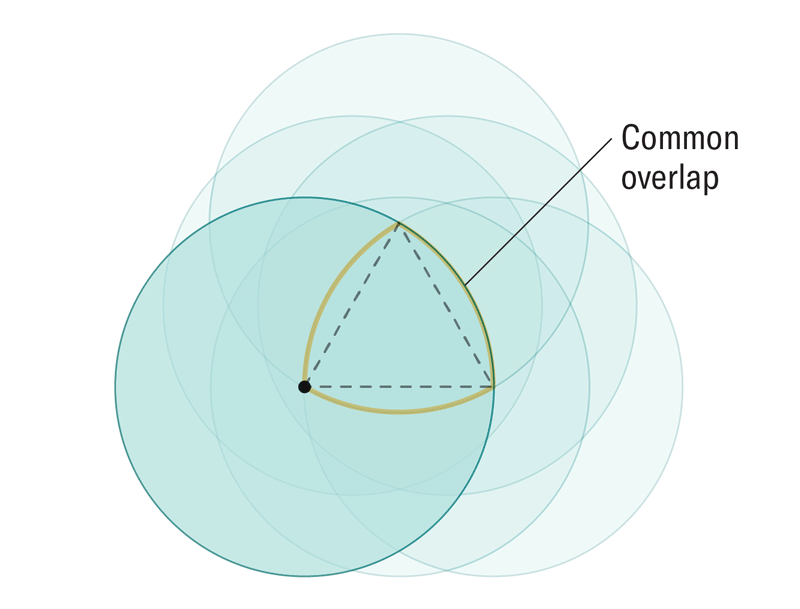
為了在二維中表示這一點，再次繪製一個等邊三角形，然後在三角形的一個頂點周圍繪製一個圓，半徑與三角形的每條邊一樣長。然後想象移動該圓，使其中心點沿著三角形的輪廓移動，沿著每條邊向上移動並經過每個頂點，然後再返回到起點。當圓移動時，有些位置它始終佔據。移動圓的無限多個位置的交集形成了一個熟悉的形狀：勒洛輪，它是勒洛三角形的推廣。“透過這樣做，您基本上得到了與勒洛三角形相同的結構，只是在這裡我們取無限多個球體的交集，而不是僅僅三個或四個，”曼尼託巴大學的數學家和該研究的合著者 Andrii Arman 解釋說。

這種簡單、可計算的技術可以揭示任何維度中恆定寬度的物體，只要我們圍繞其拖動圓的邊界針對每個維度正確選擇即可。根據這項新研究，在任何維度中選擇這個邊界都歸結為一個基本配方。在二維中，我們圍繞一個較小的四分之一圓而不是等邊三角形來追蹤圓。在三維中，我們將其進一步縮小，從球體的四分之一縮小到八分之一，並且這種模式透過增加 2 的冪擴充套件到更高的維度。在n維度中製作這樣一個邊界，並沿著它移動相應的n維球體，描繪出一個更高維度的維恩圖，作者證明該維恩圖的中心必須始終具有恰好為 2 的寬度，從而在任何維度中產生他們的新形狀。

這種無限而非有限的構建形狀的方法不僅確保了恆定寬度，而且還使得在更高維度空間中計算它們的體積變得簡單明瞭。相比之下，先前的構造涉及估計多個變數的積分，而最新的工作僅涉及兩個變數，而與形狀的維度無關。“在高維度中估計體積真的很難，”Kalai 說，但“整個[證明]相當簡單且非常優雅。”

新物體的體積比n維球體小 0.9ⁿ 倍，這意味著體積隨著每個額外維度呈指數級減小。雖然當移動到更高維度空間時，形狀的大小以越來越快的速度減小，但它們並不是保持恆定寬度的最小可能物體。Bondarenko 說，“據推測，邁斯納體在三維中具有最小的可能體積”，並補充說，“我們的結果僅比此大 0.14%。”

Kalai 認為，使用無限級數在更高維度中建立這些形狀“可能是[一個新]時代在恆定寬度集合研究中的曙光。”他總結說，隨著最初的問題現在得到驗證，“我們正處於未知的領域”，但憑藉這些新方法，“我們有希望解決許多新問題。”