在過去的幾年裡,我搬了好幾次家。一次又一次,我不得不測量房間或傢俱,然後檢查我是否能像計劃的那樣安排好一切。當我們使用捲尺、摺疊尺或直尺時,我們不會質疑我們測量的物體是否可測量。只要某物不是無限延伸的,我們就應該能夠為其指定長度、面積或體積。這正是數學家們所假設的——直到 19 世紀末,一切都發生了變化。
長期以來,如果你想測量幾何物體,你會像我搬家時那樣做:拿出捲尺就開始測量。誠然,如果你想確定複雜曲線下的面積,任務就變得更加困難。隨著 17 世紀微積分的發展,數學家艾薩克·牛頓和戈特弗裡德·威廉·萊布尼茨以積分和導數的形式提供了新的測量工具,可以用來精確地確定幾何圖形的大小。但在 200 多年的時間裡,沒有人真正問過自己應該如何測量物體。
19 世紀末,當專家們試圖將數學建立在穩定的基礎上時,集合論成為了基石。該理論提出,一切事物——包括幾何形狀和複雜的微分方程——都可以追溯到基本集合。但是,如果幾何形狀只不過是集合,那麼我們必須找到如何測量抽象集合的方法。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
讓我們以數軸上 0 到 1 之間的區間為例,記為 [0, 1]。它包含無限多個實數,但是,為了我們的目的,我們假設它的長度對應於一釐米。數學家喜歡在沒有單位的情況下進行計算,因此定義區間 [0, 1] 的長度為 1。類似地,區間 [0, 2] 的長度為 2,依此類推。
當然,專家們並沒有簡單地決定這一點,而是根據某些規則推匯出來的。為了建立這些規則,他們試圖總結長度、面積或體積等度量應具有的所有直觀屬性。即,空集的度量應為零;移動物體時,物體的度量不會改變;不重疊物體的度量等於各個物體度量的總和。從這三個簡單的結論出發,可以定義各種維度,包括上述的長度維度,這符合我們的直覺。
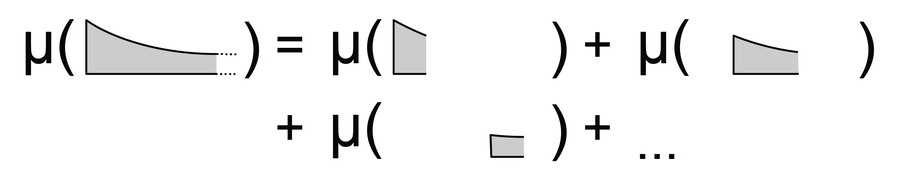
要計算不重疊集合的度量,您可以將各個集合的度量相加。
Stephan Kulla/Wikimedia Commons(CC BY-SA 3.0)
這個過程可能看起來相當繁瑣:畢竟,您憑直覺就知道結果。然而,這種方法使得更廣泛地測量量成為可能,即使是那些沒有幾何概念的量。
抽象量的度量
當數學家最初對度量感興趣時,他們最初研究的是函式(即,定義兩個變數x和y之間關係的表示式或規則)。您可能還記得中學時,可以透過積分來確定函式下方的面積。例如,您可以使用黎曼積分,其中您形成上限和下限和來確定曲線下的面積。例如,請參見下圖中的藍色條,它們表示如何將 x 軸劃分為可以加在一起以計算總面積的小區間。
但是,如果函式極其複雜,會發生什麼情況呢?例如,如果你看一下不連續的狄利克雷函式,那麼用通常的積分概念就走不了多遠。如果 x 是有理數,則狄利克雷函式 χ(x) 的值為 1。否則,該函式的值始終為零。繪製此函式的圖形,您將看到 χ(x) 由沿直線 y = 1 和 y = 0 的無數個點組成。由於函式的圖形僅由單獨的、不相連的點組成,因此不可能使用黎曼積分。
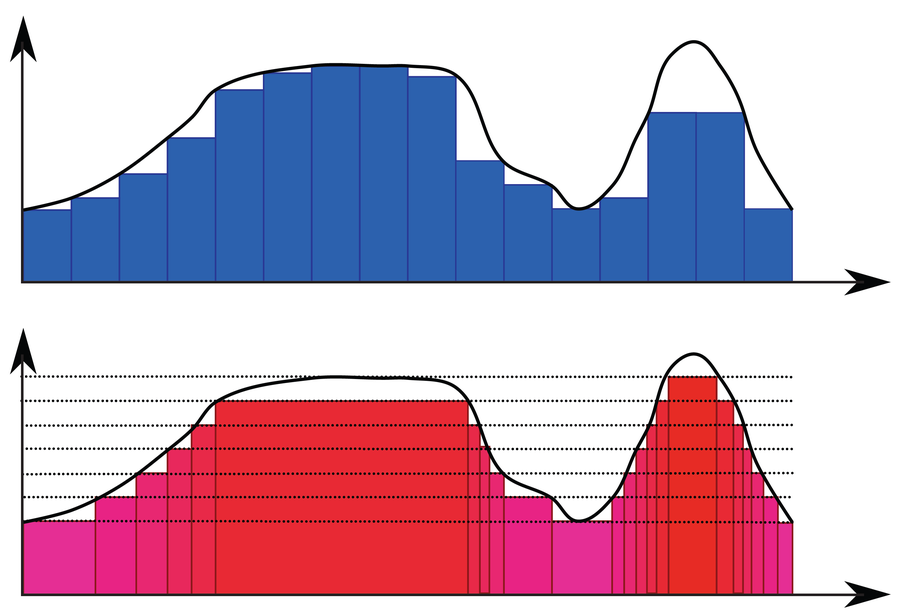
黎曼積分和勒貝格積分都透過分解來定義積分。黎曼積分垂直分解(藍色),而勒貝格積分水平分解(紅色)。
Svebert/Wikimedia Commons(CC0 1.0)
相反,您需要轉向數學家亨利·勒貝格於 1902 年提出的勒貝格積分。在這種情況下,y 軸被劃分為小區間——如上圖中的紅色條所示。要計算面積,您必須確定 x 軸上相應區間的寬度。
對於所有不像狄利克雷函式那樣不連續的普通函式,勒貝格積分和黎曼積分提供完全相同的結果。勒貝格積分的優點在於它還可以為更復雜的情況指定面積。
因此,回到狄利克雷函式,在區間 [0, 1] 中,讓我們使用勒貝格積分並將 y 軸劃分為小段。函式的點僅位於 y = 0(對於無理數 x 值)或 y = 1(對於有理數 x 值),因此結果是 0 乘以範圍 [0, 1] 中所有無理數的長度,加上 1 乘以 [0, 1] 中所有有理數的長度。此時,我們需要度量理論來為抽象集合指定長度:[0, 1] 之間的無理數和 [0, 1] 之間的有理數。由於只有可數個有理數(有關該陳述的證明,請參見下圖和說明),因此它們的度量為零。[0, 1] 之間剩餘無理數的度量因此必須為 1(因為 [0, 1] 中的所有實數加起來的度量為 1)。因此,狄利克雷函式在零和一之間的下方面積為 1 x 0 + 0 x 1 = 0。
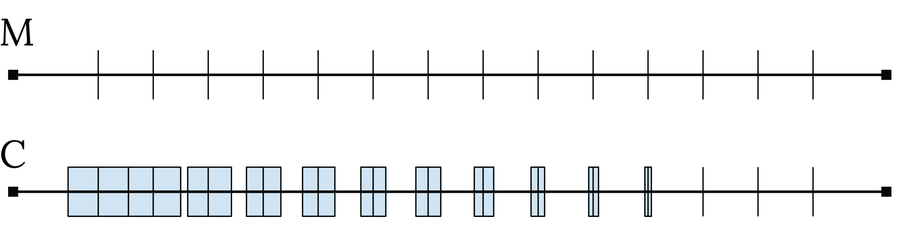
考慮集合 M = {m1, m2, m3, ..., mi, ...}。由於 M 包含可數個元素,因此可以用整數索引 i 對它們進行編號。要確定維度 μ(M),可以進行估計。為此,在每個 mi 周圍形成一個小區間 Ii,其寬度 ε/(2i) 逐漸減小且任意小:Ii = [mi − ε⁄(2i+1), mi + ε⁄(2i+1)],並從中形成一個新集合 C = {I1, I2, I3,..., Ii, ...}。因此,C 類似於原始集合,只是它不包含單個點 m,而是包含小區間。總的來說,C 的度量必須至少與 M 的度量一樣大:μ(M) ≤ μ(C)。現在可以透過假設 ε 選擇得足夠小以至於區間 Ii 永不重疊來計算 C 的度量。然後,該度量對應於區間的加法長度:μ(C) = ∑i∞ε/(2i) = ε。這意味著 M 的度量必須小於或等於 ε:μ(M) ≤ ε。由於 ε 可以選擇為任意小,因此 M 的度量必須為零。這證明對於每個可數集,μ(M) = 0 成立。
馬農·比肖夫/光譜科學
測量問題出現
勒貝格積分在 1902 年引發了所謂的測量問題。專家們想知道是否有可能為每個量指定一個度量。僅僅三年後,數學家朱塞佩·維塔利給出了一個令人沮喪的答案:不,有些集合非常不規則,無法測量。
當維塔利構造了一個具體的集合,任何型別的度量都失敗時,他意識到了這一點:維塔利集,以他的名字命名。他從簡單的開始,考慮了 0 到 1 之間的所有數字的集合。然後,他將這個集合劃分為不同的區域:如果 a – b 的結果是有理數,則兩個數字 a 和 b 最終會落在同一範圍內。例如,所有自然數和所有有理數都在同一區域。在另一個區域中,有 0.2 + √0.2 和 0.3 + √0.2,依此類推。因此,維塔利將區間 [0, 1] 劃分為(不可數)無限多個小部分。
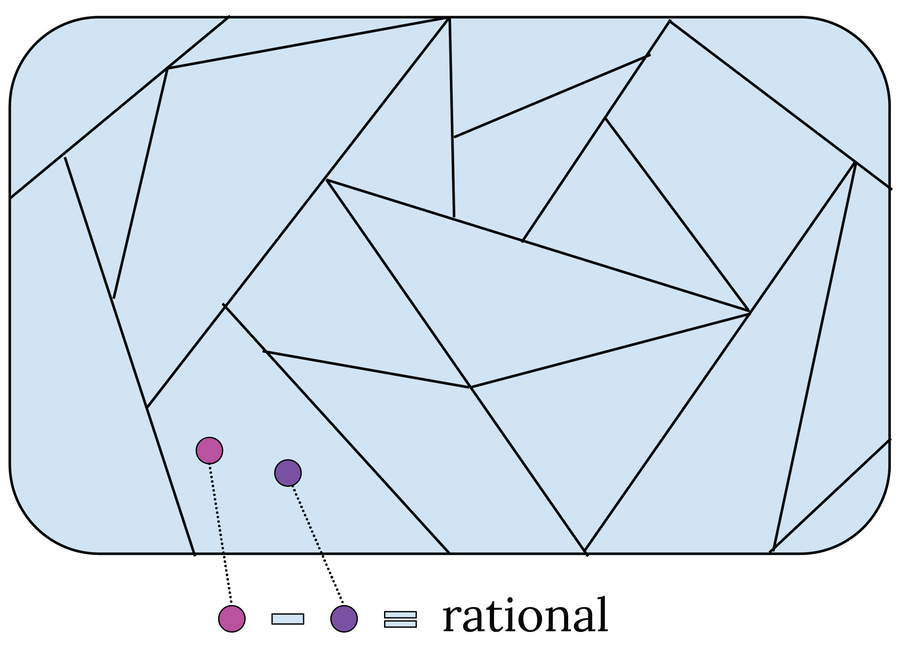
為了構造維塔利集,將區間 [0, 1] 分解為各個區域。如果兩個數字(粉紅色和紫色圓圈)的差是有理數,則它們在同一範圍內。
馬農·比肖夫/光譜科學
下一步,他從每個範圍中精確選擇一個代表 r,並將所有這些代表插入到一個新集合 V 中。因此,集合 V 包含不可數個元素,因為區間 [0, 1] 有不可數個無限個細分。然後,維塔利轉向了一個技巧:他研究瞭如果集合 V 被有理數 p 移動會發生什麼,p 的值介於 [–1, 1] 之間:Vp = V + p。結果,有理數 p 被新增到 V 中的每個元素 r 中。透過這種方式,維塔利生成了可數無限個集合 Vp,這些集合包含 [–1, 2] 之間的數字。原因是 V 包含 [0, 1] 之間的數字,而 p 添加了來自區間 [–1, 1] 的值。
這一切都非常技術性,但別擔心;我們快到了!維塔利集 V* 包含所有 Vp,正如我們將看到的,它超出了度量理論的概念。我們知道 V* 的度量至少與區間 [0, 1] 的度量一樣大(因為 V* 至少與 V 一樣大,V 的範圍為 0 到 1)。另一方面,維塔利集小於或等於區間 [–1, 2]。這意味著 μ ([0, 1]) = 1 ≤ μ(V*) ≤ μ([–1, 2]) = 3。因此,維塔利集的度量必須介於 1 和 3 之間。
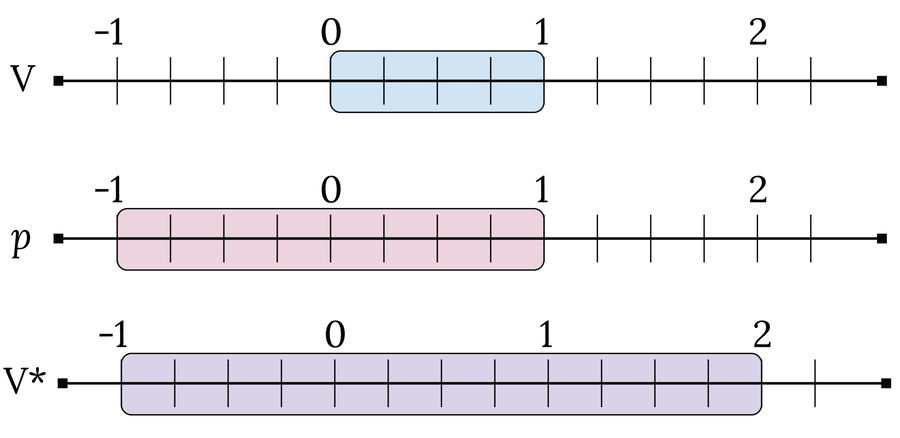
集合 V 的範圍從 0 到 1,而值 p 的範圍從 –1 到 1。因此,維塔利集 V* 的範圍從 –1 到 2。
馬農·比肖夫/光譜科學
現在您也可以直接計算維塔利集的度量:μ(V*) = ∑pμ(Vp),因為只有可數個 p。集合 Vp 包含 [p, 1 + p] 之間不可數個元素,因此 μ(Vp) 是一個大於零的有限數。事實上,所有 Vp 的大小都相同——p 的不同值僅表示平移,這與集合的大小無關。這意味著 μ(Vp) = μ(V)。因此,維塔利集的度量為 μ(V*) = ∑pμ(V),即一個常數 μ(V) 被無限次求和。這種計算的結果始終是無窮大——無論常數 μ(V) 有多小。這意味著:μ(V*) = ∞,這與上述不等式 1 ≤ μ(V*) ≤ 3 相矛盾。
總會存在不可測量的量
令人驚訝的結果並不意味著我們的數學運算有誤。相反,維塔利集非常複雜,無法為其指定度量。因此,維塔利證明並非所有量都是可測量的;也存在“不可測量”的量。
這個結果本身就令人震驚。畢竟,維塔利集是有限的,並且僅包含實數值。如果將此結果轉移到二維集合,您會得到更奇怪的結果:例如,您可以透過將球體分解為不可測量的集合來使球體的表面積翻倍。
幸運的是,不可測量的量極其罕見。例如,在物理學中,它們不會出現——畢竟,物體的分解受到原子大小的限制。您必須構造不可測量的量才能遇到它們。然而,它們又無處不在:即使在簡單的數值區間中,也潛伏著不可測量的部分。事實證明,擺脫此類量並非易事。人們將不得不改變數學的公理——以及基礎——以防止不可測量量的出現。
本文最初發表於《光譜科學》,經許可轉載。
