“一個形狀最少可以有多少個角才能鋪滿平面?” 數學家加博爾·多莫科斯在吃披薩時問我。他這個看似簡單的問題是關於平鋪的幾何形狀,也稱為鑲嵌——形狀(稱為瓦片或單元)的排列,這些形狀填充表面,沒有間隙或重疊。人類對鑲嵌的痴迷至少可以追溯到古代蘇美爾,在蘇美爾,鑲嵌在建築和藝術中佔據著突出的地位。但在思想家們擺弄瓦片的幾個世紀裡,似乎沒有人認真思考過鑲嵌的瓦片的最少頂點(線條相交的尖角)數量是否有限制。直到多莫科斯出現。追逐角越來越少的瓦片最終使他和他的小團隊發現了一種全新的形狀。
那是 2023 年的夏天,多莫科斯和我坐在黑狗餐廳的木製野餐桌旁,這是一個舒適的披薩和葡萄酒場所,離布達佩斯技術與經濟大學只有幾個街區,多莫科斯在那裡擔任教授。他穿過桌子,拿起一張紙質披薩選單,翻過來,露出了空白的背面,並示意我拿一支筆。仲夏的天空呈現出橙色和靛藍的色調,我用三角形填滿了選單。多莫科斯期待地看著。“你可以使用曲線,”他終於說道。我開始用圓形填滿頁面,當然,圓形本身無法填充空間。但多莫科斯眼前一亮。“哦,這很有趣!”他說。“繼續,你可以混合形狀。儘量保持平均角數儘可能低。”
我繼續畫下去。我的圓形頁面充滿了越來越絕望的、彎彎曲曲的形狀。多莫科斯的瑪格麗塔披薩早已消失,但他還沒有完全準備好離開。快速瀏覽一下我粗略的圖畫還不足以確定其平均角數,更不用說可能的最小值了。但正確的答案一定比三角形的三個角要少——否則,這個問題就太無聊了。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於發現和塑造我們當今世界的想法的具有影響力的故事。
這個觀察似乎讓這位數學家感到滿意,他透露真正的答案是二。“這是一個簡單的問題,”他說。“但是 3D 呢?”
“對我來說,這是一種工具,可以合理地描述比簡單地將多面體粘合在一起更廣泛的物理相關事物。”——數學家海姆·古德曼-施特勞斯
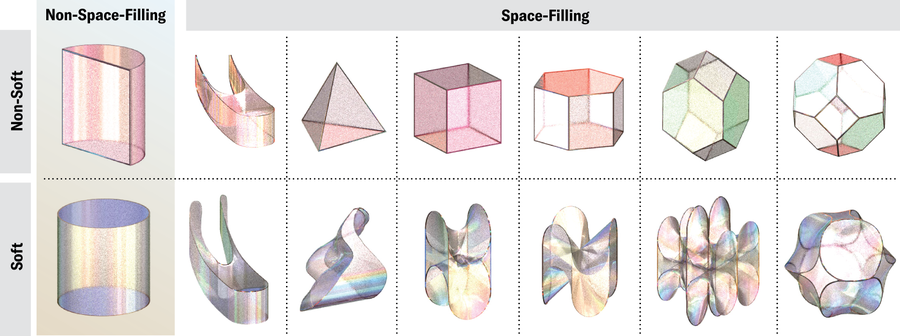
現在,在披薩店的那個晚上過去一年多之後,多莫科斯有了答案。找到答案是一個激動人心、令人沮喪的挑戰,最終促使他和三位同事發現了“軟細胞”,這種形狀可以組合在一起,完全填充平面或三維空間,並且角儘可能少。在二維中,軟細胞有兩個角,由曲線橋接。但在 3D 中,這些彎曲的、幾乎有機的形狀根本沒有角。一旦研究人員確定了新的形狀,他們就開始在各處看到它們——在自然界、藝術和建築中。這些結果現已發表在期刊PNAS Nexus上。
儘管軟細胞以前沒有被數學家分類——沒有人注意到或在學術論文中命名它們——但它們在藝術和自然界中比比皆是,從扎哈·哈迪德“曲線女王”的建築,到斑馬條紋的形狀。多莫科斯的研究生克里斯蒂娜·雷戈斯在鸚鵡螺殼的腔室中發現了第一個天然 3D 軟細胞,鸚鵡螺殼已成為展示數學和生物學融合的標誌性物體。“它們一直就在我們眼前,”雷戈斯說。與如此著名的形狀的聯絡讓多莫科斯擔心他的團隊會被搶先。他發誓讓他的合作者保密,直到他們的發現準備好發表。(它在九月釋出。)在披薩課結束時,他甚至拿走了紙質選單,將其摺疊起來並放入口袋。只是為了安全起見。
史密斯學院的數學家約瑟夫·奧魯爾克(未參與這項研究)表示,事後看來,軟細胞的存在應該是顯而易見的。但是,他說,想到提出這樣的問題,“甚至想象你可以用沒有頂點的物體來鋪滿空間”,這才是原創。“我發現這非常令人驚訝和非常聰明。”
阿肯色大學的數學家海姆·古德曼-施特勞斯是平鋪方面的專家,他說:“對我來說,這是一種工具,可以合理地描述比簡單地將多面體粘合在一起更廣泛的物理相關事物。” “只要看看一杯啤酒中的泡沫,你就會知道他們正在研究一些東西。”
多年前,多莫科斯開發了一種數學工具,用於根據鑲嵌的平均屬性而不是單個單元的形狀來描述鑲嵌。這個想法源於對天然馬賽克(如破裂的岩石表面)的研究。使用平均值可以捕捉鑲嵌的本質,而不會施加不自然的剛性。
當多莫科斯和雷戈斯探索控制馬賽克平均屬性的規則時,他們意識到了一件事:似乎不可能將每個瓦片的平均頂點(角)數降到兩個以下。由此,人們很容易意識到,單瓦片——僅用自身副本填充平面的瓦片,例如蜂巢的規則六邊形或棋盤的方塊——不可能少於兩個頂點。以前沒有人認識到這條規則。
當多莫科斯和雷戈斯找不到任何關於該主題的先前工作時,兩人意識到他們手頭有一些有趣的東西。但是,當涉及到將他們的發現轉化為正式的數學規則時,他們感到幾何學知識不足。他們招募了同樣在布達佩斯技術與經濟大學工作的幾何學家阿科斯·G·霍瓦特來幫助他們。
霍瓦特很快設計出一種演算法,可以將平面的多邊形平鋪變形為僅具有兩個頂點的形狀的平鋪。利用它,該團隊從三角形、六邊形和矩形的規則平鋪中設計出圓形、柔軟的雙頂點瓦片。他們使用的六邊形瓦片看起來像六邊形,其中兩個角被拉伸出來,其餘部分被磨成圓形的小突起。從正方形衍生的瓦片更加多樣化。一種看起來像變形的正方形,但其他瓦片類似於木瓦、魚鱗、扁豆和鯨魚的尾葉。從三角形衍生的兩種型別的瓦片看起來有點像小山和船帆。
然後,多莫科斯說,“我們開始幻想 3D 中會是什麼樣子。”
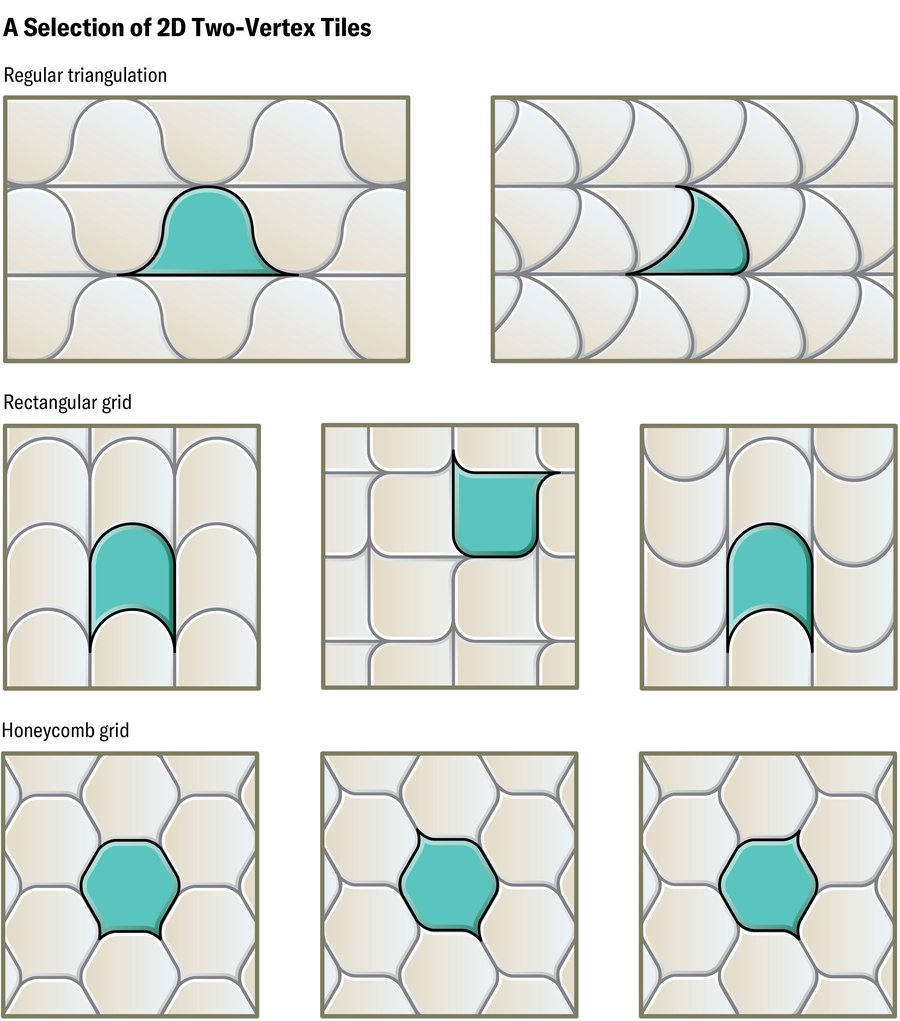
Jen Christiansen;資料來源:“軟細胞和貝殼的幾何形狀”,作者:加博爾·多莫科斯、阿蘭·戈裡利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(瓦片參考)
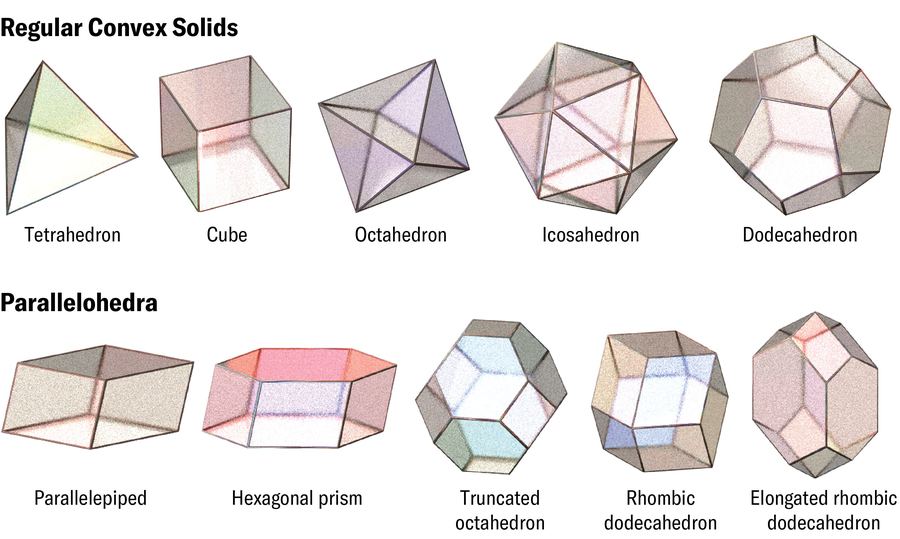
至少從柏拉圖時代起,人們就一直在想象 3D 鑲嵌。他圍繞五個正凸多面體(四面體、立方體、八面體、二十面體和十二面體)的鑲嵌構建了他的宇宙模型。柏拉圖認為,前四種形狀的鑲嵌應該構成土、氣、水和火的古典元素。十二面體是宇宙的物質。柏拉圖的錯誤不僅僅在於這種深奧的宇宙學。只有立方體實際上可以作為單瓦片填充 3D 空間——用一個形狀的精確副本——而沒有間隙和重疊(除非空間本身是彎曲的)。但是,擠壓和拉伸成立方體的平行六面體(面為六個平行四邊形的形狀)也可以填充空間。1885 年,俄羅斯晶體學家葉夫格拉夫·費多羅夫編目了一組五種形狀,稱為平行多面體——可以無任何旋轉地堆疊在一起的 3D 形狀。這些形狀包括立方體和蜂巢中常見的六稜柱,以及更深奧的菱形十二面體、拉長十二面體和截角八面體。
所有這些形狀都是具有平面和直邊的多面體。但是,具有曲線的 3D 形狀也可以填充空間——儘管現成的例子只是稍微彎曲並且具有明顯的角。具有啟發意義的是,已知的例子都源於對自然的疑問,而不是抽象數學。1887 年,英國數學家威廉·湯姆森(也稱為開爾文勳爵)提出了一個難題:體積相等的細胞或氣泡的什麼排列方式可以最大限度地減少它們之間介面的表面積?換句話說,什麼是最佳泡沫?
Violet Frances
開爾文的第一個解決方案是略微變形的截角八面體的鑲嵌。在 1994 年的一篇論文中,當時都在都柏林聖三一學院的物理學家丹尼斯·韋爾和羅伯特·費蘭用兩種不同的變形多面體的鑲嵌擊敗了開爾文的結構。2018 年,由塞維利亞大學的路易斯·M·埃斯庫德羅和西班牙綜合系統生物學研究所的哈維爾·布塞塔領導的一個生物物理學家團隊發現了一種名為盾片的形狀,類似於變形的蜂巢,人體的上皮細胞會呈現這種形狀,以便在需要彎曲和彎曲的組織中進行最佳堆積。儘管如此,似乎沒有人問過空間填充固體可以有多少個角。匈牙利團隊向 3D 的飛躍最初是一種信念的飛躍。“我們一點頭緒都沒有。甚至沒有預感,”多莫科斯說。

Violet Frances
當三人最終確定了一個只有兩個角的空間填充 3D 形狀時,多莫科斯認為他們找到了答案。“我完全痴迷於這件事,”他說。“我寫了一篇論文,證明三維空間中的最小角數是兩個。” 這個證明源於多莫科斯認為微不足道的一個簡單假設。但是,隨著幾個月過去了,他慢慢開始意識到這個假設並非那麼微不足道——甚至可能是錯誤的。“他想在聖誕節、新年夜,以及之後更晚的時候把這篇文章發給我和阿科斯,”雷戈斯回憶說,忍俊不禁。“然後他找到了一個零角的例子。就是這樣。” 這種形狀本身就是一個證明:在三維空間中,可以用根本沒有角的物體來鑲嵌空間。
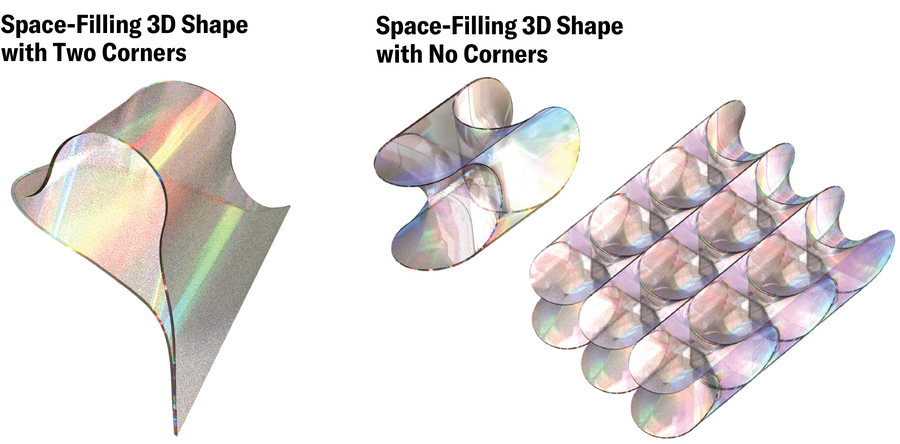
Violet Frances;資料來源:“軟細胞和貝殼的幾何形狀”,作者:加博爾·多莫科斯、阿蘭·戈裡利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(參考)
找到第一個軟細胞解決了一個問題,並開啟了無數個問題。例如,研究人員想知道是否可能存在只有一個角的空間填充形狀。多莫科斯最終找到了一種。當他在黑板上為雷戈斯和霍瓦特畫出草圖時,他們“感到厭惡”,他說。這是一個醜陋的形狀——一個沒有對稱性的變形形狀,看起來像是外星人夢寐以求的東西。但在某種程度上,雷戈斯從這種醜陋中瞥見了可能性。“我有一天看到了它,然後意識到,”她說。“我們可以做這種邊緣彎曲的事情,並創造柔軟感。”
雷戈斯的直覺是,她可以透過彎曲普通尖角多面體的邊緣來建立軟細胞。在三個邊緣相交的每個頂點處,她會抓住兩個邊緣,並將它們強制彎曲成平行於頂點之前剩餘邊緣的曲線。3D 空間中的封閉實體必須包圍 4π 度的曲率,曲率通常集中在頂點處。雷戈斯正在將曲率塗抹在邊緣上。“我花了幾天幾夜才相信她所做的事情並非完全是垃圾,”多莫科斯說。
雷戈斯在用數學語言描述她的彎曲邊緣方法時遇到了困難。但隨後她意識到,這個過程可以歸結為圖論中一個容易解決的二維問題。每個多面體都有一個對偶——另一個多面體,其面對應於其邊,反之亦然。該團隊表明,如果可以沿著多面體對偶的邊緣找到一條恰好訪問其每個頂點一次的路徑(稱為哈密頓迴路),那麼也可以將該形狀變形為無角的空間填充軟細胞。
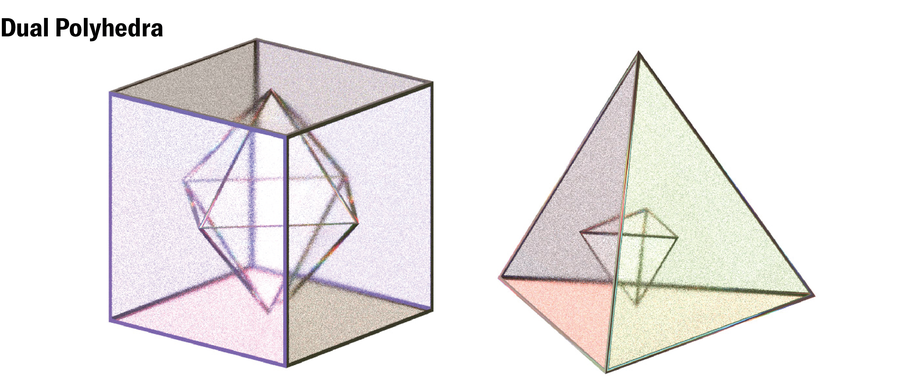
Violet Frances
有了這個條件,霍瓦特終於可以編寫一個數學 3D 邊緣彎曲演算法。透過將無限類別的多面體平鋪對映到軟平鋪,他證明了無限類別的軟細胞的存在。換句話說,對於每個可以用自身填充空間的多面體(具有平面多邊形面的 3D 形狀),也必須存在彎曲的軟細胞。
對於奧魯爾克來說,邊緣彎曲演算法是論文中最美妙和最重要的部分。這種優雅來自於將兩個完全不同的數學領域結合在一起。哈密頓迴路純粹是組合的(與計數的數學有關)——它們“與幾何無關”,奧魯爾克解釋說。“但是在這裡,你非常專注於幾何。然而,你需要這個組合條件。所以我發現這非常好。”
Violet Frances;資料來源:“軟細胞和貝殼的幾何形狀”,作者:加博爾·多莫科斯、阿蘭·戈裡利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(參考)
當數學家們開始理解二維軟細胞的數學原理時,他們開始意識到這些形狀不僅僅存在於他們的草圖和筆記中。“它們就在我們眼皮底下,”多莫科斯說。該團隊開始在各處看到雙頂點瓦片的平面馬賽克,從肌肉組織到斑馬條紋。有一次,在布達佩斯的一次散步中,雷戈斯甚至在金屬安全格柵的彎曲交叉處看到了它們。
與此同時,三人組發現了越來越多的 3D 軟細胞——雷戈斯在多莫科斯的第一個形狀(變形的立方體)的基礎上添加了四個平行多面體和四面體的變形版本。但是,研究人員很難在現實世界中識別出這些 3D 軟細胞。這種情況在多莫科斯第一次發現邊緣彎曲的立方體大約一年後發生了變化,他意識到他以前在某個地方見過它——不是在自然界中,而是在建築中。
大約十年前,建築師維基·桑多爾和維也納大學的一群學生為太陽馬戲團表演中心構思了一個 необычный 設計。這座建築從未建成,但在建築界引起了一些關注。它的基本構建模組是一個形狀,看起來幾乎與多莫科斯的立方軟細胞完全相同。
桑多爾的專案最初是圍繞“平衡”主題的熱身練習,這位現任奧地利技術研究所的建築師說。這座建築必須是模組化的,因此他們將其劃分為立方體模組,每個模組由不同的人設計。巧合的是,該設計的靈感來自一種名為 gömböc 的自平衡形狀,該形狀由多莫科斯和結構力學研究員彼得·瓦爾科尼在 2006 年發現。桑多爾和她的隊友喜歡 gömböc 的細而肥的對比,並希望找到一種類似的形狀,可以將不同的模組組合在一起。他們在網球的 C 形曲線中找到了答案。“如果你沿著 C 形切割,那麼你會得到一個非常薄和一個非常肥的元素。而 gömböc 遵循了這個原則,”桑多爾說。事實證明,將彎曲表面切割成管狀或稜柱狀是構建軟細胞的好方法——不僅在理論或設計中,而且在自然界中也是如此。
雷戈斯憑直覺發現了第一個天然 3D 軟細胞。有一天,她突然給多莫科斯發了一張鸚鵡螺殼橫截面的照片。多莫科斯回覆說,這是一個二維軟細胞的很好的例子。雷戈斯回覆說:不,它們是 3D 軟細胞。“它看起來一點都不軟,”多莫科斯心想。“我的意思是,它有角。” 但雷戈斯堅持己見。因此,多莫科斯買了兩個鸚鵡螺殼,並將它們交給雷戈斯和霍瓦特進行檢查。他們玩弄貝殼大約 30 分鐘後放棄了。多莫科斯說,即使他們可以透過觀察貝殼來說服自己,“你也不能將貝殼作為附件傳送給論文。”
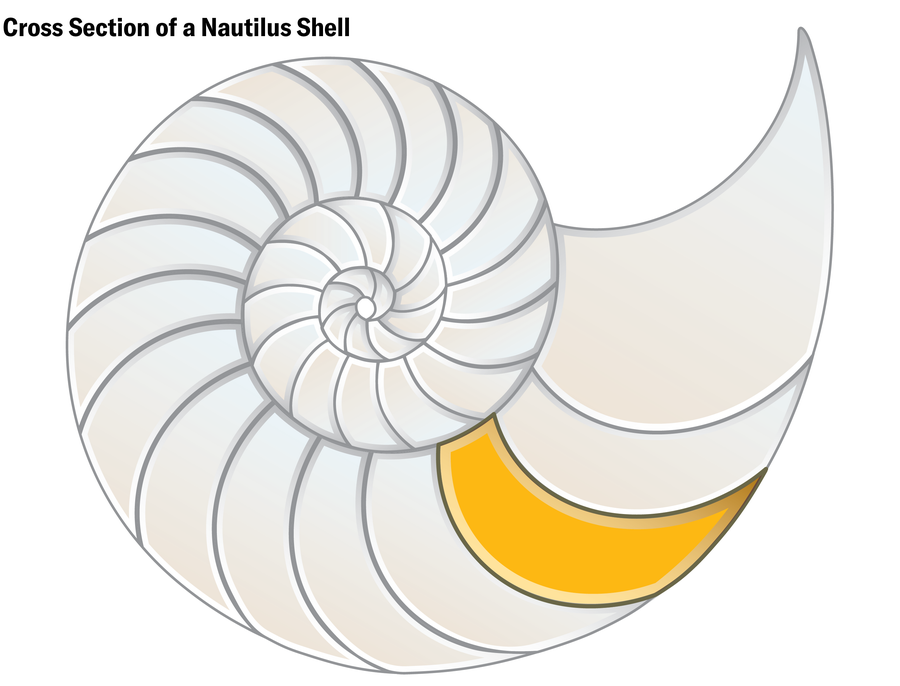
Jen Christiansen;資料來源:“軟細胞和貝殼的幾何形狀”,作者:加博爾·多莫科斯、阿蘭·戈裡利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(參考)
如果不是蘇格蘭鄧迪大學的達西·湯普森動物學博物館釋出了一組免費提供的微型 CT 掃描,這個想法可能就此作罷。多莫科斯在網上找到了掃描結果,並花費數小時“在貝殼內部爬行”,尋找角。他找不到任何角。
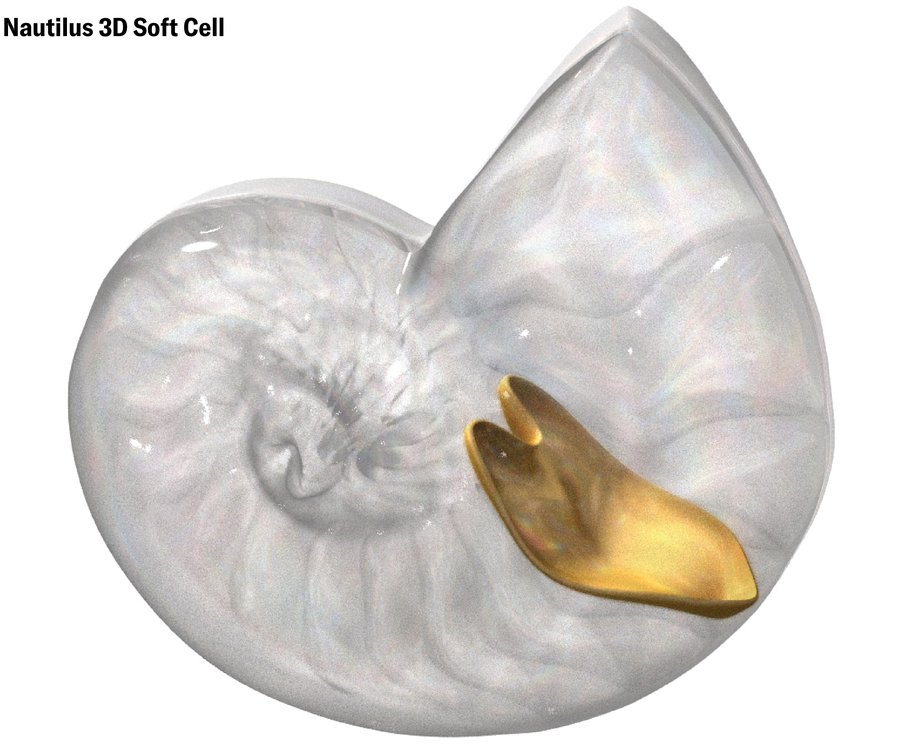
Violet Frances;資料來源:“軟細胞和貝殼的幾何形狀”,作者:加博爾·多莫科斯、阿蘭·戈裡利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(參考)
團隊中沒有人對貝殼一竅不通。但多莫科斯認識一個懂行的人:阿蘭·戈裡利,牛津大學的物理學家和應用數學家,他研究過有腔室的貝殼。多莫科斯很緊張地告訴小組外的人這個專案,尤其是現在他們已經在鸚鵡螺殼內發現了軟細胞——鸚鵡螺殼是喜歡自然形狀的數學家最喜歡的形狀。很容易搶先他們的想法並先發表。但多莫科斯認識戈裡利幾十年了,所以他決定冒險給他打電話。不久之後,他和雷戈斯登上了一架飛往牛津的飛機。
戈裡利立即被鸚鵡螺殼內軟細胞的發現所吸引。“我發現自然界中的形狀以這種方式發展是很自然的,因為形成尖角代價很高,”戈裡利說。生物細胞是柔軟的,表面張力自然會使它們變圓,除非生物體消耗能量來構建可以保持更尖形狀的剛性結構。而且,生物體內的細胞希望以少量間隙有效地填充空間。
在他們在牛津瘋狂的三天以及隨後的幾個月中,戈裡利和匈牙利人發現了越來越多的自然和藝術界的軟細胞例子。斑馬條紋、河流入海口、洋蔥橫截面、貝殼、麥穗、紅細胞、植物和真菌都類似於二維軟細胞。在建築方面,二維軟細胞為建築師扎哈·哈迪德的許多建築物賦予了未來主義的有機形式。它們也出現在日本藝術家葛飾北齋的榻榻米和服裝草圖中,葛飾北齋創作了著名的 1831 年畫作《神奈川衝浪裡》,以及光學藝術運動的“祖父”維克多·瓦薩雷裡的藝術作品中。
戈裡利還幫助該團隊找到了另一個 3D 軟細胞的例子:菊石殼的腔室。然後,雷戈斯設計了一個幾何模型,該模型從第一性原理產生了類似於貝殼示例的形狀。像鸚鵡螺殼中的軟細胞那樣,透過將稜柱與彎曲表面相交,可以輕鬆地製造出軟細胞——這與桑多爾和她的團隊用於設計太陽馬戲團建築的過程相呼應。“令人高興的是,建築師也憑直覺達到了 [這個過程],”戈裡利說。“根據我們的理解,他們是出於同樣型別的要求而達到這個目標的:他們想軟化結構。”
古德曼-施特勞斯說,這項工作建立了一個探索軟形狀的“有用詞彙”——這個詞彙開啟了新的數學問題。存在哪些類別的軟單瓦片?哪些軟形狀組可以和不可以平鋪空間?多莫科斯想知道柔軟度與非週期性(在不建立重複圖案的情況下平鋪平面的能力)有何關係。去年,第一個非週期性單瓦片(用自身副本填充空間但從不重複圖案的單個形狀)的發現成為頭條新聞。多莫科斯和雷戈斯很好奇如果他們將邊緣軟化演算法應用於 “幽靈”平鋪(第一個真正的非週期性單瓦片)會發生什麼。但他們驚訝地發現,其軟化版本無法單獨平鋪平面。

Jen Christiansen;資料來源:“手性非週期性單瓦片”,作者:大衛·史密斯、約瑟夫·塞繆爾·邁爾斯、克雷格·S·卡普蘭和海姆·古德曼-施特勞斯;2023 年 5 月 28 日;arXiv:2305.17743(參考)
阿肯色大學的古德曼-施特勞斯和安大略省滑鐵盧大學的克雷格·S·卡普蘭(他們都為第一個非週期性單瓦片的發現做出了貢獻)一點也不感到驚訝。卡普蘭說,數學家們才剛剛開始探索非週期性單瓦片,還有許多問題有待解答。
儘管軟細胞在自然界中似乎無處不在,但這些形狀的數學與生物學之間的聯絡目前只是一種視覺觀察。多莫科斯承認這是這項工作的一個弱點,並希望確定它們在自然界中如此普遍的原因。“論文的很大一部分是關於視覺相似性,這非常不尋常,”他說。卡普蘭說,進一步探索這種聯絡似乎很有希望。“我確實喜歡這種動機:只是簡單地聲稱自然不喜歡尖銳的特徵,所以讓我們從數學的角度來研究它。這是一個很好的開場白,你可以從中發展出豐富的理論。”
古德曼-施特勞斯說,軟細胞的概念最終可能會被證明是有用的——“不一定是今天的生物學家,而是 30 年後的生物學家”。也許軟細胞的數學最終將捕捉到一些關於軟物質的真實資訊——軟物質構成了我們世界的大部分,從我們血管中的血液到你現在可能正在閱讀的液晶顯示器。
關於軟幾何的問題特別棘手,因為它們往往會跨越學科界限。多莫科斯掙扎了幾個月才找到一家願意發表該團隊“古怪”手稿的期刊,該手稿混合了數學、藝術和生物學。古德曼-施特勞斯對此並不感到驚訝。當被問及他認為軟細胞在科學領域中屬於哪裡時,他不假思索地說。“我認為,”他說,“唯一的答案是它屬於未來。”
