編者注:本文發表於 1957 年,摘自馬丁·加德納的傳奇《大眾科學》專欄“數學遊戲”。在我們的特別數字期刊《趣味遊戲》中閱讀更多內容。
正如本雜誌的許多讀者所知,莫比烏斯帶是一種幾何奇觀,它只有一個面和一個邊緣。這種圖形是稱為拓撲學的數學分支所關注的。對數學有粗淺興趣的人可能會認為,拓撲學家是一個數學花花公子,他把時間花在製作莫比烏斯帶和其他有趣的拓撲模型上。如果他們開啟任何最近的拓撲學教科書,他們會感到驚訝。他們會發現一頁又一頁的符號,很少有圖片或圖表來緩解這種枯燥。誠然,拓撲學起源於對幾何謎題的思考,但今天它已成為抽象理論的叢林。拓撲學家懷疑那些必須透過視覺化才能理解的定理。
儘管如此,嚴肅的拓撲學研究仍然不斷產生怪異而有趣的模型。例如,考慮一下雙莫比烏斯帶。它是透過將兩條紙條放在一起形成的,像一條紙條一樣給它們一個半扭,並將它們的末端連線起來,如下面的插圖所示。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
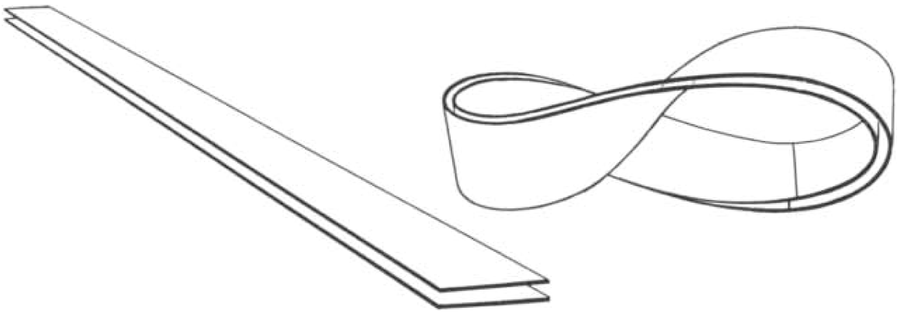
雙莫比烏斯帶是透過將兩條紙條放在一起(左),給它們都扭轉半圈,然後按照右側直線指示的方式連線起來製成的。
詹姆斯·埃格爾森
我們現在擁有看起來像是兩個巢狀的莫比烏斯帶。事實上,您可以透過將手指放在帶子之間並繞著它們一直移動,直到回到您開始的點來“證明”有兩個獨立的帶子。一隻在帶子之間爬行的蟲子可以無限期地繞著它們轉圈,始終在一個帶子上行走,而另一個帶子沿著它的背部滑動。它永遠不會發現“地板”與“天花板”相遇。一隻聰明的蟲子會得出結論,它正在兩條獨立帶子的表面之間行走。
然而,假設這隻蟲子在地板上做了一個標記,並繞著帶子轉圈直到再次到達標記。它會發現標記不在地板上,而是在天花板上,並且需要第二次繞著帶子轉圈才能在地板上找到它!這隻蟲子需要相當的想象力才能理解地板和天花板都是同一條帶子的一個面。看起來像是兩條巢狀的帶子實際上是一條大的帶子!當您將模型展開成大的帶子時,您會發現很難將其恢復到原來的形狀。
當帶子呈雙重形式時,它的兩個獨立的邊緣彼此平行執行;它們繞著模型轉兩圈。想象一下,這些邊緣被連線起來,並且帶子是由薄橡膠製成的。那麼您將得到一個管子,可以充氣使其成為環面(拓撲學家對甜甜圈表面的術語)。連線的邊緣將形成一條圍繞環面盤繞兩圈的閉合曲線。這意味著可以沿著這樣一條曲線切割環面,從而形成雙莫比烏斯帶。
事實上,雙帶與一條在末端連線之前被給予四個半扭的單帶相同。可以將環面切割成具有任何期望的偶數個半扭的帶子,但不可能切割它以產生具有奇數個這種扭轉的帶子。這是因為環面是一個雙面表面,只有具有偶數個半扭的帶子才是雙面的。雖然雙面表面可以透過切割單面表面來製成,但反之則不可能。如果我們希望透過切割沒有邊緣的表面來獲得單面帶(具有奇數個半扭的帶子),我們必須求助於切割克萊因瓶。艾爾伯特·W·塔克和赫伯特·S·貝利在《拓撲學》中描述了這個非凡的單面瓶。[大眾科學; 1950 年 1 月]。
簡單的莫比烏斯帶是透過在連線末端之前給紙條扭轉半圈製成的。能否以某種方式拉伸帶子,直到這個邊緣變成三角形?答案是肯定的。第一個設計出這種模型的人是布萊恩特·塔克曼,他是摺疊彈性多面體藝術的四位先驅之一 [“數學遊戲”;1956 年 12 月]。下面的插圖展示瞭如何切割、摺疊和貼上一張紙來建立塔克曼的模型。
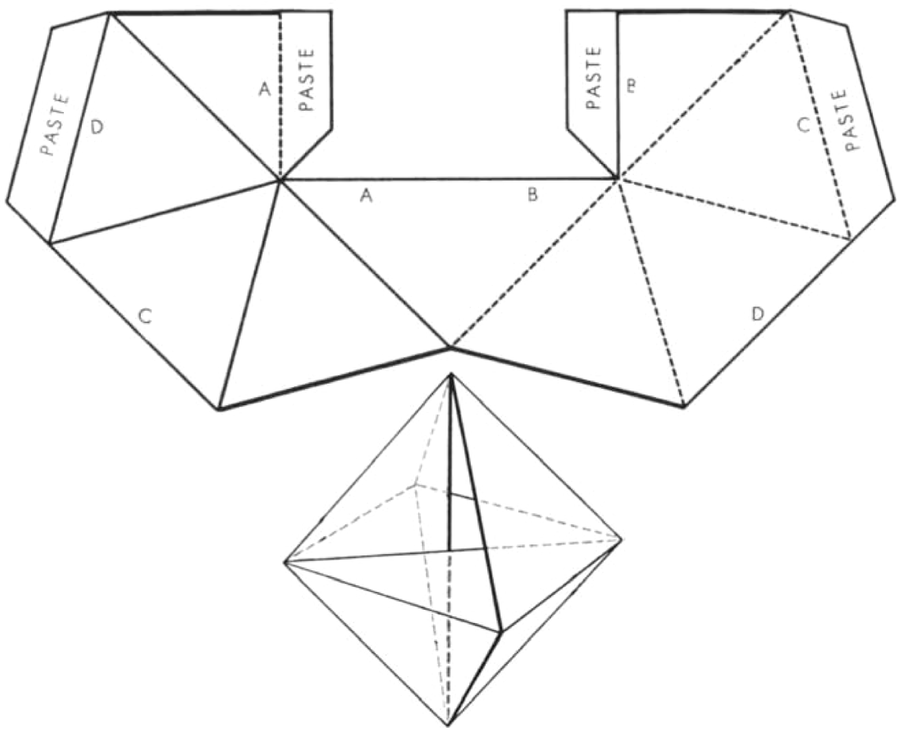
帶有三角形邊緣的莫比烏斯帶是由布萊恩特·塔克曼設計的。如果將平面圖形重新繪製,最好按比例放大,則可以按如下方式組裝尺寸多面體模型。首先,剪下圖形。其次,沿著實線“向下”摺疊。第三,沿著虛線向相反方向摺疊。第四,透過將膠水塗在四個標籤上,連線邊緣 A 和 A、B 和 B、C 和 C 以及 D 和 D。完成的多面體中的粗線描繪了莫比烏斯曲面的三角形邊界。
詹姆斯·埃格爾森
表面不僅可以有一個或兩個面;它們的拓撲結構也可能因邊緣的數量和結構而異。這些特徵不能透過扭曲表面來改變;因此,它們被稱為拓撲不變數。讓我們考慮邊緣不超過兩個的表面,以及邊緣是簡單的閉合曲線或普通單結形式的表面。如果表面有兩個邊緣,它們可以是彼此獨立的或連結的。在這些限制範圍內,我們可以列出以下 16 種表面(不包括無邊緣表面,如球體、環面和克萊因瓶):
單面,單邊緣
1. 邊緣是簡單的閉合曲線。
2. 邊緣是打結的。
雙面,單邊緣
3. 邊緣是簡單的閉合曲線。
4. 邊緣是打結的。
單面,雙邊緣
5. 兩個邊緣都是簡單的閉合曲線,未連結。
6. 兩個邊緣都是簡單的閉合曲線,已連結。
7. 兩個邊緣都是打結的,未連結。
8. 兩個邊緣都是打結的,已連結。
9. 一個邊緣是簡單的;一個是打結的,未連結。
10. 一個邊緣是簡單的;一個是打結的,已連結。
雙面,雙邊緣
11. 兩個邊緣都是簡單的閉合曲線,未連結。
12. 兩個邊緣都是簡單的閉合曲線,已連結。
13. 兩個邊緣都是打結的,未連結。
14. 兩個邊緣都是打結的,已連結。
15. 一個邊緣是簡單的;一個是打結的,未連結。
16. 一個邊緣是簡單的;一個是打結的,已連結。
紙模型很容易構建,以說明這 16 種表面中的每一種的示例。下面描繪了表面 1 到 12 的模型。讀者可能會喜歡嘗試構建剩餘四個表面的模型,其圖紙將在下個月的專欄中出現。
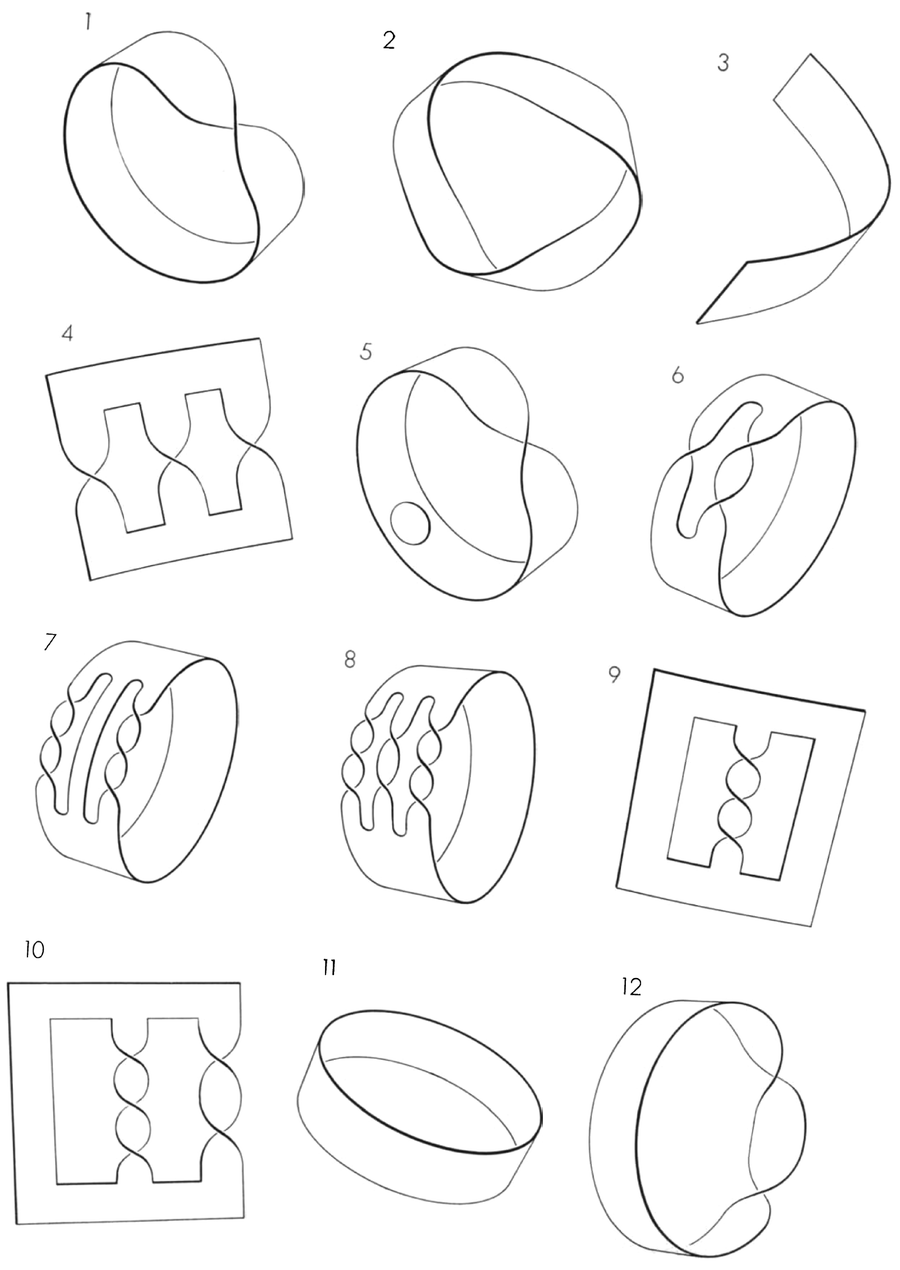
拓撲模型是 16 個模型中的 12 個,這些模型可以用邊緣不超過兩個的表面以及簡單閉合曲線或單結的邊緣製成。簡單的莫比烏斯帶是 1。
詹姆斯·埃格爾森
當用剪刀以某種方式切割其中一些模型時,結果令人震驚。正如幾乎所有玩過莫比烏斯帶的人都知道的那樣,縱向將帶子對半切割並不會像人們可能預期的那樣產生兩條獨立的帶子,而是一條大的帶子。(這條大的帶子有四個半扭;因此它可以製成前面描述的雙莫比烏斯帶。)不太為人所知的是,如果您從一個邊緣和另一個邊緣之間三分之一的位置開始切割,並一直切割到回到起點,則莫比烏斯帶會展開成一條大的帶子,並與一條小的帶子連結在一起。
將表面 12 對半切割會產生兩條相同大小的互鎖帶子,每條都與原始帶子完全相同。將表面 2 對半切割會產生一條大的帶子,帶子上有一個結。後一種特技是一本小冊子的主題,該小冊子在 1880 年代在維也納廣為銷售。這本小冊子揭示了在布帶上打結而無需藉助魔術的秘密。
在說兩個邊緣“連結”時,我們指的是像鏈條中兩個鏈環一樣連結的方式。要分離這些連結,必須開啟一個鏈環並將另一個鏈環穿過開口。然而,有可能以這樣一種方式將兩條閉合曲線互鎖,以至於為了分離它們,不需要將一條穿過另一條的開口。最簡單的方法如下面的插圖中的上部曲線所示。這些曲線可以透過在 A 點將黑色曲線穿過自身來分離。

互鎖的曲線可以分離,而無需將一條穿過另一條的開口。頂部的曲線可以透過在 A 點將黑色曲線穿過自身來分離。
詹姆斯·埃格爾森
插圖底部的三條閉合曲線也是不可分離的,但沒有連結。如果您移除任何一條曲線,其他兩條曲線是自由的;如果您連結任何一對曲線,它會釋放第三條曲線。順便說一句,這種結構在拓撲學上與著名啤酒品牌的熟悉的三環商標相同。這些被稱為博羅梅安環,因為它們構成了文藝復興時期義大利博羅梅奧家族的紋章。
