2024年10月12日

數學謎題：用紙牌屋玩建築師

作者：漢斯-卡爾·埃德爾

喬萬用總共 90 張撲克牌搭建了這五座紙牌屋。現在他想用正好 100 張牌搭建一座大型紙牌屋。這樣的紙牌屋存在嗎？

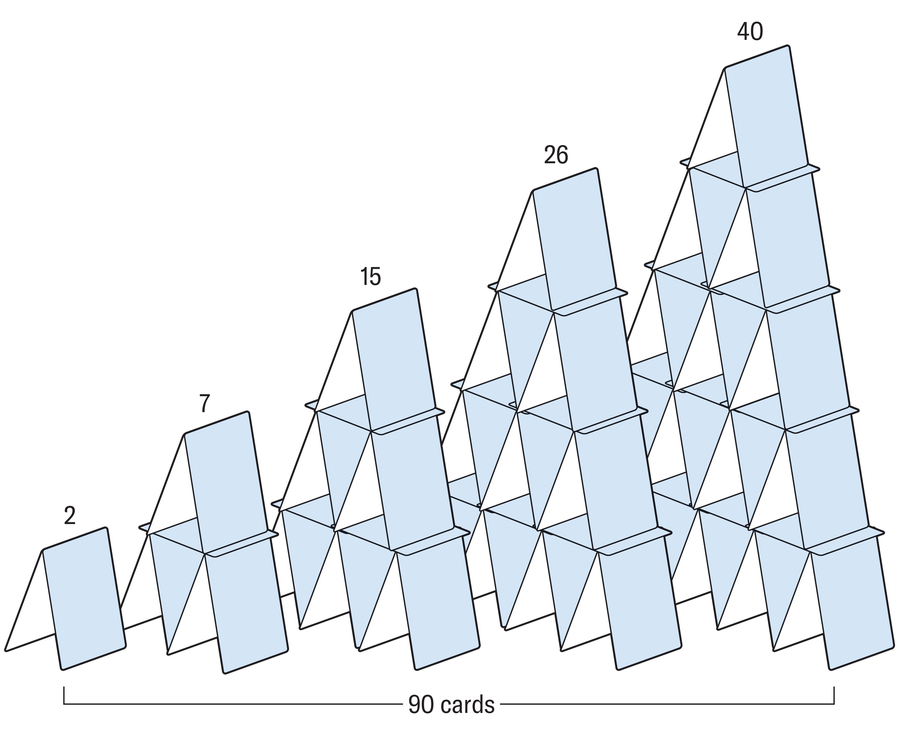
Graphic shows five triangle-shaped houses of cards composed of the following numbers of cards: 2, 7, 15, 26 and 40. The total number of cards shown is 90.

阿曼達·蒙塔涅斯；來源：漢斯-卡爾·埃德爾/《科學光譜》(參考文獻)

你可以用正好 100 張牌搭建一座紙牌屋；它將有八層。

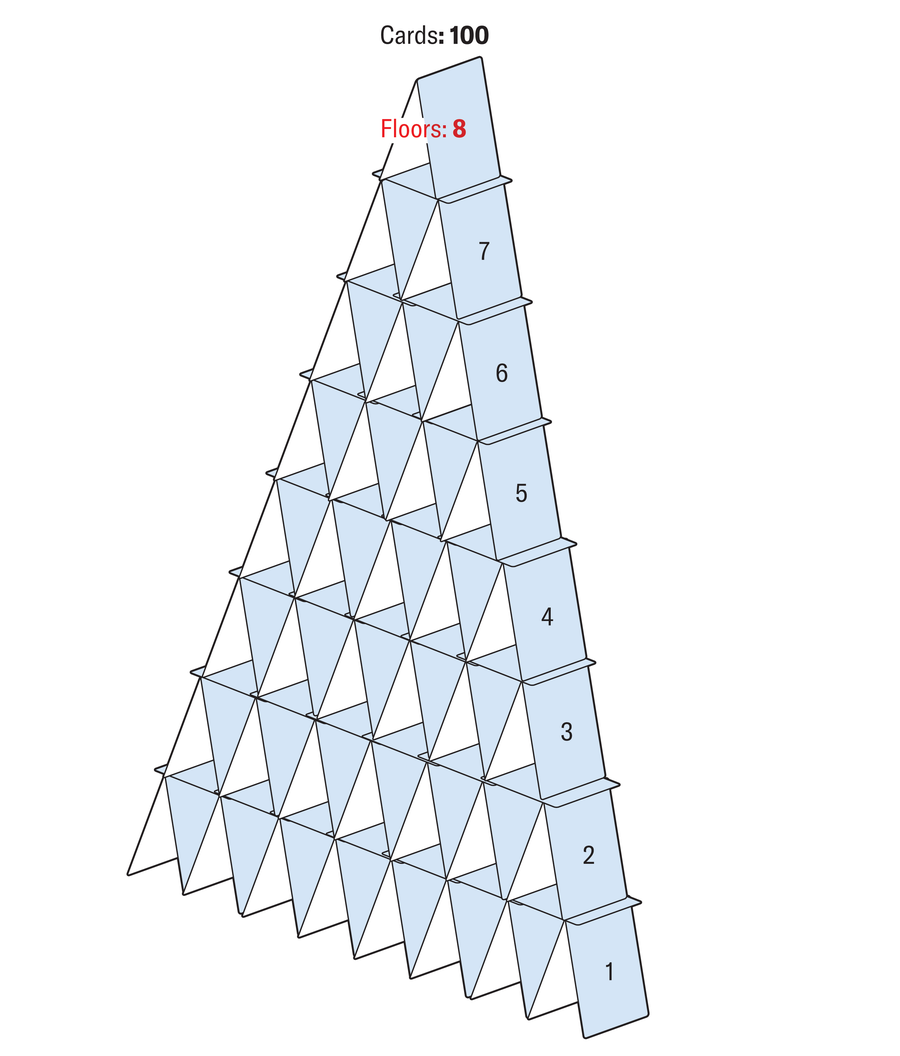
Graphic shows a triangle-shaped house of cards that has eight floors and is composed of 100 cards.

阿曼達·蒙塔涅斯；來源：漢斯-卡爾·埃德爾/《科學光譜》(參考文獻)

紙牌的數量逐層以恆定序列增加。如果你想證明謎題的答案，你必須證明 100 是這個序列中的一項。

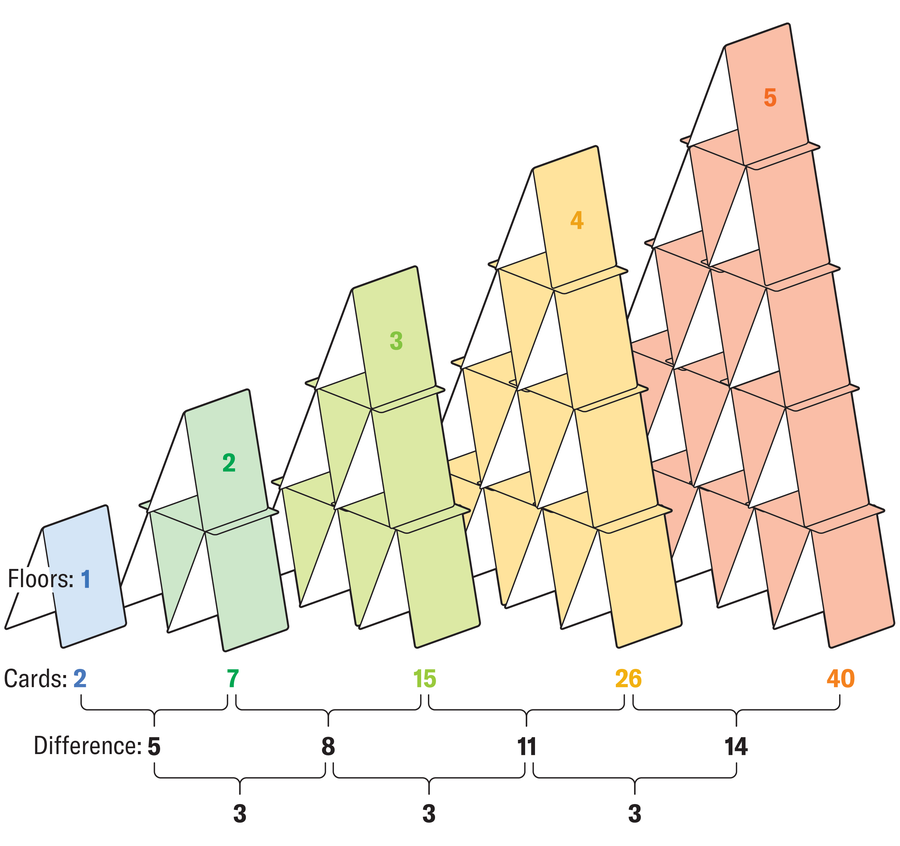
Graphic shows five triangle-shaped houses of cards composed of 2, 7, 15, 26 and 40 cards. The number of floors in each house is highlighted: 1, 2, 3, 4 and 5. The increase in the number of cards at each step is shown (7 minus 2, 15 minus 7, and so on), followed by the difference between each of those increases (8 minus 5, 11 minus 8, and so on), which equals 3.

阿曼達·蒙塔涅斯；來源：漢斯-卡爾·埃德爾/《科學光譜》(參考文獻)

這是一種方法。因為項之間的差值始終變化相同的量——“二階差分”是恆定的——你可以得出結論，紙牌數量 K 和層數 x 的序列可以用 K = ax2 + bx + c 形式的二次方程表示。

首先，確定 a、b 和 c 的值。這可以使用三個方程組來實現

A system of three equations is created from the first three terms in the house of cards sequence: 2 equals a times 1 squared plus b times 1 plus c; 7equals a times 2 squared plus b times 2 plus c; 15 equals a times 3 squared plus b times 3 plus c. Subtracting the first equation from the second one gives an equation designated capital A: 5 equals 3a + b. And subtracting the second equation from the third one gives an equation designated capital B: 8 equals 5a plus b. Subtracting equation capital A from equation capital B allows you to calculate that a equals 1.5. And inserting that into equation capital B lets you find that b equals 0.5. Combining those values for a and b with your original first equation, 2 equals a plus b plus c, reveals that c equals 0.

阿曼達·蒙塔涅斯；來源：漢斯-卡爾·埃德爾/《科學光譜》(參考文獻)

有了 a、b 和 c 的值以及計算出的 K = 100 值，你現在可以解二次方程。

Graphic 5 alt text: Now you can insert the number of cards K equals 100 into the quadratic equation K equals a times x squared plus b times x plus c. Using the values you found earlier, you get the equation 100 equals 1.5 times x squared plus 0.5 times x plus 0. Divide both sides by 1.5 and move all terms to one side to find x squared plus one third times x minus 200 thirds equals 0, which is equivalent to x minus 8 times x plus 25 thirds equals 0. Therefore, x equals 8 or negative 25 thirds.

阿曼達·蒙塔涅斯；來源：漢斯-卡爾·埃德爾/《科學光譜》(參考文獻)

x 的值之一是自然數，它讓你可以用正好 100 張牌搭建一座紙牌屋。

我們很樂意聽到你的來信！請傳送電子郵件至 games@sciam.com 分享你的體驗。

這個謎題最初出現在《科學光譜》中，經許可轉載。

0
© .