核心概念
數學
加法
計數
謎題
引言
你是否曾經使用數學作為工具來解決有趣的問題?在 20 世紀 70 年代,數學通常是透過簡單的練習冊來教授的。一位老師正在尋找一種方法來幫助他的學生在數學和邏輯中獲得更多樂趣。因此,他開發了現在被稱為周長幻方三角形謎題的東西。嘗試一下——並開始以全新的方式思考計數,享受一些樂趣!
背景
計數是如此普遍,以至於我們忘記了它與更廣泛的數字研究領域(稱為算術)的聯絡。我們可以將計數視為重複加一:當你將一個物體新增到另一個物體時,你有兩個物體。再加一個,你就有了三個,以此類推。加法是加數字的過程。加法的結果稱為和。對於較小的數字,你可能會使用計數來找到和。例如,當你得到三,想加上二時,你可以從三開始數兩個數字,得到五。經過大量的練習,你通常可以記住 1 到 10 的數字之和——此時,玩數字,找到構成特定和的所有方法會很有趣。
關於支援科學新聞
如果你喜歡這篇文章,請考慮訂閱以支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,你正在幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。
數學謎題和遊戲可以是一種練習使用數字的有趣方式。謎題還提供了有趣的途徑來培養戰略性和邏輯性思維。透過一些試錯,你通常可以開始找到新的策略來更快地完成謎題。這些正是數學家使用的技術:從小處著手,並嘗試在答案序列中找到模式。然後,這些模式用於預測更大謎題的答案。
如果這一切都太抽象,請嘗試此活動中提供的謎題!它可能會使學習算術的過程變得清晰。
材料
兩張 9 英寸 x 12 英寸的紙,例如結構紙或工藝紙(如果可能,請選擇對比色)
鉛筆或記號筆
尺子
剪刀
四分之一硬幣或其他類似大小的圓形物體
21 個硬幣、小方塊或其他小型可堆疊物體
更多紙張(可選)
準備工作
在紙上畫一個大三角形(你可以使用尺子來幫助畫直線)。
在三角形的每個角上用四分之一硬幣描出一個圓。現在在三角形的每條邊的中間描出一個圓。你應該有六個圓。
在第二張紙的底部畫六個大小與三角形上繪製的圓相似的圓。
剪下這些圓,並將其編號為 1 到 6。這些圓將被稱為數字盤。
保留第二張紙的頂部。你將用它來寫下你的結果。
步驟
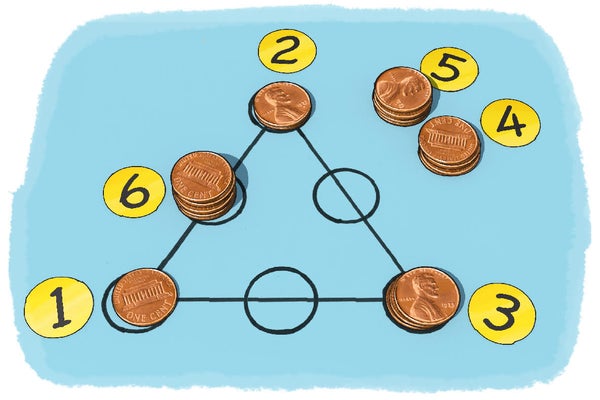
在畫有三角形的紙上,使用 21 個硬幣在每個圓上建造塔。每個圓必須至少有 1 個硬幣,但沒有兩個塔的高度相同。你能做到嗎?
不斷嘗試,直到找到解決方案!
數數每個塔中的硬幣數量。按從小到大的順序寫下每個總和。你對這組數字有什麼看法?
移動塔或重建塔,直到你能滿足另一個要求:用於在三角形的每一邊上建造三個塔的硬幣總數必須相同。例如,如果在三角形的一側排列的圓中建造 1、5 和 3 個硬幣的塔,則在該側使用了 1 + 5 + 3 = 9 個硬幣。在相鄰側排列 1、2 和 4 個硬幣的塔將不起作用,因為 1+ 2 + 4 = 7——不像第一側那樣是 9。(請注意,1 個硬幣的塔位於此三角形的角上,因此它對兩條邊都有貢獻。)如果你嘗試用 1、2 和 6 作為相鄰側,那將起作用,因為 1 + 2 + 6 = 9。現在你可以放置剩下的一個塔,並檢查此三角形的第三側的三個塔中是否使用了 9 個硬幣。嘗試一下!你找到解決方案了嗎?
如果這不是一個解決方案,請思考。你能重新排列幾個塔並得到一個解決方案嗎?
如果使用抽象數字對你來說更容易,請用數字盤替換塔。然後,每個數字盤代表一個硬幣塔。數字盤上寫的數字會告知你該塔中的硬幣數量。
每邊使用 9 個硬幣是可能的!你找到解決方案了嗎?是否可以通過幾種方式排列塔,使每邊都使用 9 個硬幣?
你能否排列硬幣,使每邊使用 10 個、11 個甚至 12 個硬幣?
附加題:證明沒有每邊使用 8 個或更少硬幣的解決方案,或者證明沒有每邊總共使用 13 個或更多硬幣的解決方案。
附加題:此活動中提出的謎題稱為“三階周長幻方三角形”。要將其擴充套件到更高階的周長幻方三角形,首先畫一個新的三角形。像第一次一樣在角落上新增圓,但這次在角落之間的每一側新增兩個圓。對於這個謎題,你將需要九個數字盤。將其編號為 1 到 9。就像在之前的謎題中一樣,你需要找到將數字盤放在圓上的方法,以便此三角形每側的數字之和都相同。數學家稱此三角形為四階三角形,因為它每側有四個數字。解決此謎題後,繼續使用五階三角形(在角落之間新增三個圓並剪下 12 個數字盤),然後使用六階三角形,以此類推。
附加題:你能否建立一種策略來快速找到此類謎題的解決方案?
觀察和結果
你是否發現,如果需要製作六個高度不同的塔,你只能將 21 個硬幣排列成 1、2、3、4、5 和 6 個硬幣的塔?你是否能想出排列塔的方法,使三角形每邊使用的硬幣之和對於所有三邊都相同?每邊總共可以使用 9、10、11 和 12 個硬幣。
為了在每邊使用總共 9 個硬幣,你將 1、2 和 3 個硬幣的塔放在三角形的角上。6 個硬幣的塔放在 1 和 2 個硬幣的塔之間,因為 1 + 2 + 6 = 9。5 個硬幣的塔位於 1 個硬幣的塔和 3 個硬幣的塔之間,因為 1 + 3 + 5 也等於 9。2、4 和 3 個硬幣的塔填滿了第三行。請注意,對於此解決方案,最小的塔放在角落裡。
要排列塔,使每邊使用 12 個硬幣,首先在三角形的角上排列最高的塔(那些有 6、5 和 4 個硬幣的塔),並在中間的圓中填充。將你剩下的最小的塔(高 1 個硬幣)放在兩個最高的塔(每個 5 和 6 個硬幣)之間。你是否看到剩下的最小的塔(高 2 個硬幣)位於需要中間塔的最高的塔之間(每個塔有 6 和 4 個硬幣)?
你可以用來找到每邊都有 10 個硬幣的解決方案的策略是列出所有可以透過新增三個不同數字得到 10 的方法。你會發現 3 + 2 + 5 = 10、5 + 4 + 1 = 10 和 1 + 6 + 3 = 10。你能看到 3、5 和 1 是這些總和中的兩個的一部分嗎?這意味著這些位於三角形的角上。你可以使用相同的策略來找出如何放置硬幣,以便每邊使用 11 或 12 個硬幣。
你是否想知道你怎麼知道每邊使用 8 個硬幣是不可能的?每邊使用 8 個硬幣,你將在三角形上使用 3 X 8,即 24 個硬幣。因為你重複使用角塔上的硬幣,所以你最多使用 1 + 2 + 3(三個最小塔的總和)或少用 6 個硬幣。換句話說,你最多可以使用 18 個硬幣。該謎題要求你使用 21 個硬幣。
更多探索 來自幻方網的周長幻方三角形
《漢諾塔》,來自《大眾科學》 統計科學:入口即化的數學,來自《大眾科學》 兒童 STEM 活動,來自科學夥伴
此活動由 科學夥伴 合作提供