我在2022年11月,一位同事隨意地問我正在研究什麼。我茫然的回答反映了當時吞噬我所有腦力的各種想法:“實際上,我認為一個重大的未解決問題的答案剛剛落入我的手中。” 在一週前,我收到一封電子郵件,要求我看看一個形狀。那是我第一次看到“帽子”,一個不起眼的多邊形,結果證明是幾十年數學探索的結晶。
這封電子郵件來自大衛·史密斯,我從一個對平鋪感興趣的小型郵件列表中認識他——平鋪是排列形狀以覆蓋平面的不同方式。史密斯不是數學家;他是一位自稱的“形狀愛好者”,在他位於英格蘭約克郡的家中,在業餘時間進行幾何實驗。在史密斯給我傳送了他一直在玩的帽子形狀後,我們開始定期通訊,花費了2022年的剩餘時間研究帽子及其屬性。2023年,我們聯絡了另外兩位研究人員,數學家查伊姆·古德曼-施特勞斯和軟體開發人員約瑟夫·塞繆爾·邁爾斯,他們也都是郵件列表的成員,並且在更廣泛的平鋪理論領域廣為人知。我們四個人繼續研究帽子,並在感覺是創紀錄的時間內,成功證明該形狀是許多人認為不可能存在的長期尋求的目標:一個非週期性單瓦片,也稱為愛因斯坦瓦片。

圖片來源:珍·克里斯蒂安森
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
事實證明,史密斯的帽子只是揭示一系列啟示的開始。當我們探索這種形狀揭示的新思想領域時,我們多次驚訝於額外的發現,這些發現進一步加深了我們對平鋪理論的理解。很快,帽子就引出了“海龜”、“幽靈”和其他奇蹟,這些奇蹟產生的見解超出了我們最初的預期。
自古代以來,瓦片就讓人們著迷,但數學家在20世紀才開始認真研究它們。所謂的平面平鋪是無限形狀的集合,它們覆蓋一個平面,沒有間隙,也沒有重疊。我將重點關注平鋪中無限多的瓦片來自有限數量的不同形狀的情況。想象一下,一些模板可以用來從無限量的紙張中切割形狀的副本。我們的目標是在無限的桌面安排剪裁件,以便桌面的每一部分都被恰好一層紙覆蓋。我們可以透過反射(翻轉紙張)、旋轉(在原地轉動)和平移(在不轉動形狀的情況下滑動形狀)的某種組合將每個剪裁件移動到位。如果我們實現了構造平鋪的目標,我們就說這組形狀“允許”平鋪,更一般地說,這些形狀平鋪了平面。
並非所有形狀集合都允許平鋪。正方形產生類似於方格紙的平鋪,以及其他圖案,因此是單瓦片:它自己平鋪平面(作為一個形狀集合)。相比之下,正五邊形本身不能平鋪平面。正八邊形也不能,儘管由正八邊形和正方形組成的二元素集合確實可以平鋪。
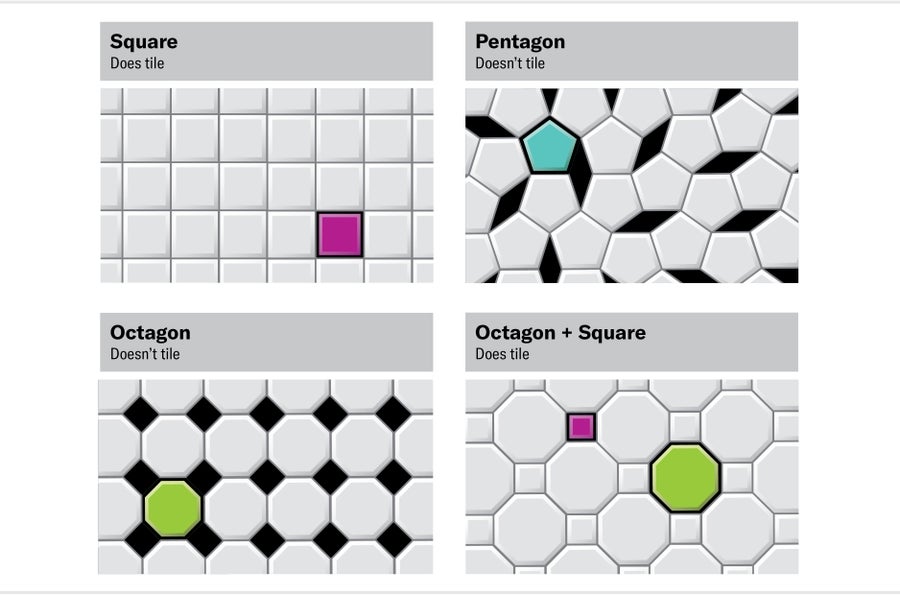
圖片來源:珍·克里斯蒂安森
我們如何確定給定的形狀集合是否可以平鋪平面?我們沒有演算法可以用來回答這個問題,實際上也不可能存在——這個問題在理論計算機科學中被稱為“不可判定的”。儘管如此,我們可以研究單個集合,並嘗試透過試錯法或其他方法構建平鋪。在這個過程中,我們經常遇到有趣的例子,說明區域性相互作用(兩個瓦片可以並排放置的不同方式)如何影響全域性行為(平鋪在各個方向無限延伸的大尺度結構)。
有多種方法可以弄清楚單個形狀是否可以平鋪平面。有些人,例如史密斯,甚至會使用計算機控制的切割工具切割形狀的物理紙質副本,並在實際的(遺憾的是有限的)桌面上擺弄它們,利用觸控的直接性來增強視覺直覺。在像史密斯這樣熟練的探索者手中,形狀會在短時間內揭示其平鋪秘密。在前帽子時代,形狀總是以兩種方式之一表現出來。
第一種可能性是形狀無法平鋪平面。作為一個快速測試,我們可能會嘗試用自身的副本完全包圍它;如果我們不能,那麼該形狀肯定不允許任何平鋪。例如,正五邊形是不可包圍的,這立即將其排除為非平鋪者。但是,儘管可包圍性提供了可平鋪性的證據,但它不是確鑿的證據:存在欺騙性的非平鋪者,它們可以被一個或多個同心層的副本完全包圍,然後不可挽回地卡住。1968年,數學家海因裡希·海施展示了一個可以被包圍一次但不能被包圍兩次的形狀,並詢問在一個非平鋪者周圍可以構建的同心環數量是否存在上限,這個數量現在被稱為形狀的“海施數”。目前的記錄保持者是一個特別難纏的多邊形,其海施數為六,由塞爾維亞諾維薩德大學的博揚·巴西奇於2020年發現。
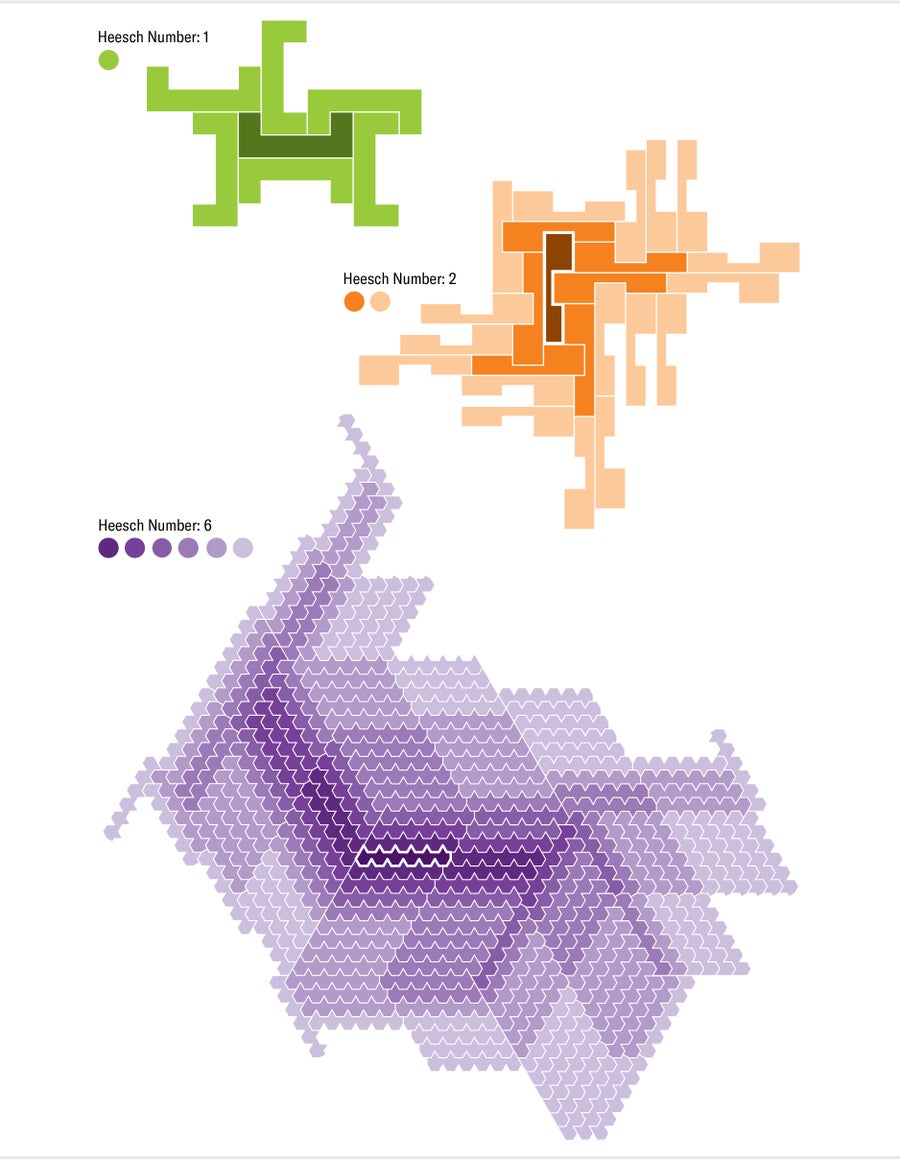
圖片來源:珍·克里斯蒂安森
第二種可能性是形狀週期性地平鋪平面。在週期性平鋪中,瓦片的排列以由無限平行四邊形網格確定的規則模式重複。我們可以使用三個資訊來描述週期性平鋪:一個稱為平移單元的有限瓦片簇,以及定義網格中平行四邊形邊長的兩條線段。我們可以將平移單元的副本滑動到網格中的每個頂點,而無需旋轉或反射它,並且這些副本將互鎖以完成平鋪。這種方法提供了一個快速測試形狀平鋪能力的方法:我們組裝候選平移單元,然後檢視它們中的任何一個是否透過在規則網格中重複來覆蓋平面。與海施數一樣,沒有人知道形狀可能需要的最小平移單元是否存在任何界限,然後才能重複平鋪平面。邁爾斯發現了當前的記錄保持者,一個形狀,其最簡單的平移單元包含10個瓦片。

圖片來源:珍·克里斯蒂安森
當史密斯開始試驗帽子時,引起他注意的是,它拒絕遵守這些選項中的任何一個。帽子顯然沒有平鋪平面:他找不到任何尺寸的平移單元的構建方法。但它也顯然沒有無法平鋪平面:透過努力,他可以用多層副本包圍帽子而不會卡住。可以想象,帽子可能是一個具有高海施數的非平鋪者,或者是一個具有大型平移單元的週期性單瓦片,但史密斯知道這種情況很少見。他聯絡我是因為他也知道還有另一種可能性,一種非常特殊,以至於需要充分考慮的可能性。
大約60年前,數學家開始想知道是否存在只能以非週期性方式平鋪平面的形狀集合——也就是說,有人可以將副本組裝成任意大的補丁,而永遠不會遇到平移單元。這樣的集合稱為非週期性的。至關重要的是,非週期性是比非週期性更強的屬性。許多形狀,包括一個不起眼的 2 × 1 矩形,可以允許週期性平鋪以及非週期性平鋪。非週期性集合沒有可能的週期性平鋪。

圖片來源:珍·克里斯蒂安森
非週期性的概念最初由郝旺在1960年代初期提出,當時他是哈佛大學的數學教授。他正在研究我們現在所說的王氏瓦片:邊緣帶有符號標籤或顏色的正方形瓦片,必須將其放置成相鄰正方形的相鄰邊緣具有相同的標記。(這些標籤是可以用幾何方式表達的等效規則的便捷速記。)旺觀察到,如果給定一組瓦片,可以找到一個矩形,其頂部和底部邊緣具有相同的標籤序列,並且其左右邊緣也匹配,則該矩形是一個平移單元,因此該集合平鋪了平面。然後他推測了逆命題:如果一組王氏瓦片允許平面平鋪,那麼就必須有可能構建這樣的矩形。換句話說,他聲稱王氏瓦片永遠不可能是非週期性的。
根據當時關於平鋪的知識,旺的猜想相當合理。然而,幾年後,旺的學生羅伯特·伯傑在這一工作的基礎上,透過構建第一個非週期性瓦片集合(一個龐大的20,426個王氏瓦片的系統)駁斥了這個猜想。順便說一句,伯傑推測應該有可能構建更小的非週期性集合,從而開啟了一個不可抗拒的數學探索,以瞭解集合可以有多小。到1971年,加州大學伯克利分校的拉斐爾·M·羅賓遜已經縮減到一組六個修改後的正方形。

圖片來源:珍·克里斯蒂安森
然後在1973年,牛津大學數學家羅傑·彭羅斯用一組只有兩個瓦片的集合取得了驚人的突破:“風箏”和“飛鏢”。
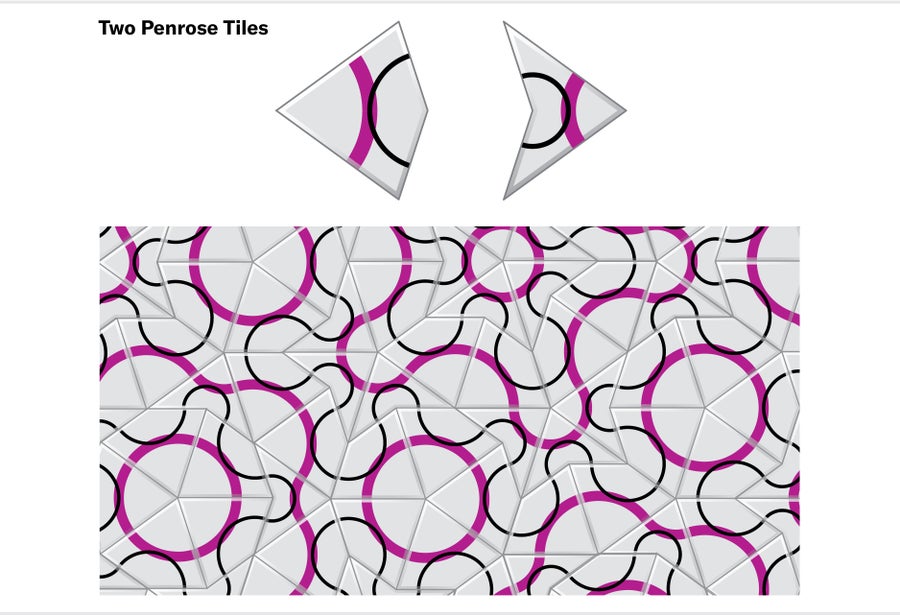
圖片來源:珍·克里斯蒂安森
彭羅斯的工作讓我們離一個顯而易見的終點線只差一步:非週期性單瓦片,一種只允許非週期性平鋪的單一形狀。這種形狀有時也稱為“愛因斯坦”,來自德語“ein stein”,意思是“一塊石頭”。(這是對“愛因斯坦”這個名字的文字遊戲,但在其他方面與著名的阿爾伯特無關。)是否存在非週期性單瓦片的問題被稱為愛因斯坦問題。
在彭羅斯之後,進展停滯了近50年。又發現了一些大小為二的集合,包括古德曼-施特勞斯發現的一個集合。一些數學家提出了單形狀解決方案,但這些解決方案不可避免地需要對遊戲規則進行小的修改。例如,索科拉爾-泰勒瓦片是一種修改後的正六邊形,可以非週期性地平鋪。問題在於,為了使這種六邊形的副本串通一氣,迫使所有平鋪都成為非週期性的,不相鄰的瓦片必須就其相對方向達成一致。如果沒有引入技巧,例如將六邊形擠壓成三維或將其分解成不連貫的碎片,就無法將這種限制烘焙到瓦片的輪廓中。
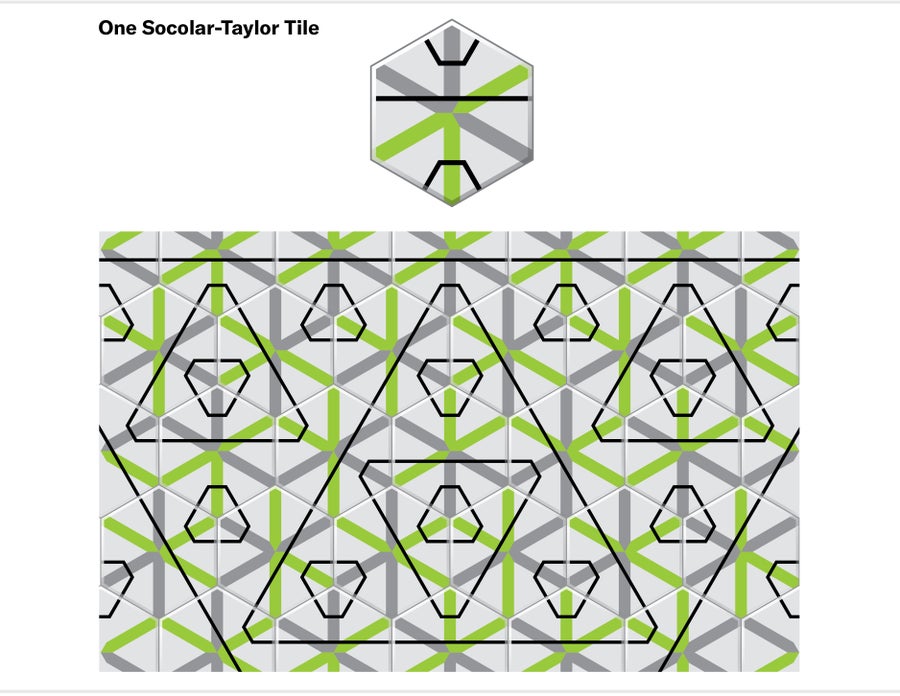
圖片來源:珍·克里斯蒂安森
即使數學中的問題尚未解決,數學家之間通常也會對其可能的答案達成廣泛的共識。例如,哥德巴赫猜想指出,每個大於二的偶數都是兩個奇素數之和。這個猜想尚未證明,但我們掌握的證據壓倒性地表明它是正確的。我一直對愛因斯坦問題著迷的一個原因是我沒有看到支援或反對它的明確證據(除了50年乾旱期的嚴峻現實)。一些數學家對非週期性單瓦片的不可能性感到無奈,但我對任何結果都持開放態度。如果說有什麼不同的話,我懷疑存在性證明可能比非存在性證明更容易處理。前者很可能是一個關於特定形狀屬性的論證,但後者必然是關於所有形狀的陳述。正如我們現在所知,在這種情況下,宇宙中存在某種正義。
史密斯並沒有專門著手尋找非週期性單瓦片,但他了解這個問題的歷史和意義。他一直在他的探索中尋找非週期性的跡象。正是史密斯在2022年11月24日的一封電子郵件中首次大膽地建議,帽子可能是愛因斯坦瓦片,並謙虛地補充說:“那豈不是很棒嗎?”
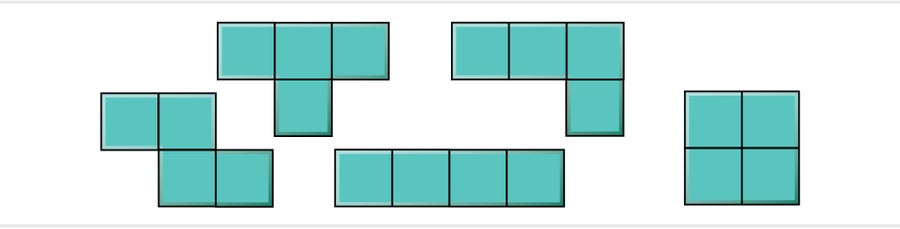
史密斯和我開始嘗試理解帽子的行為。帽子被稱為多形體:一種由一些簡單單元元素的副本組成的形狀。例如,影片遊戲俄羅斯方塊中的碎片代表了將四個正方形粘合在一起的所有方式。
圖片來源:珍·克里斯蒂安森
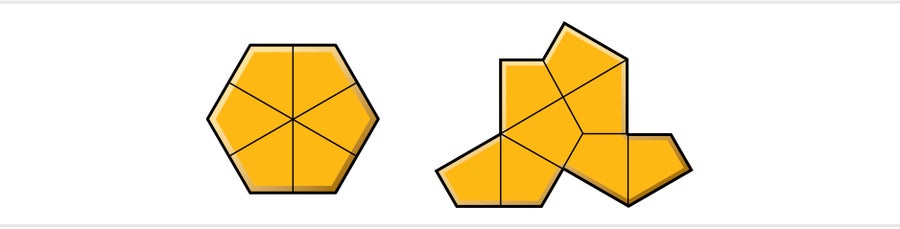
帽子由八個風箏組成。這些風箏與彭羅斯的風箏不同;史密斯透過將正六邊形切成六等份,並用連線相對邊緣中點的線段來製作它們。
圖片來源:珍·克里斯蒂安森
他知道我最近編寫了軟體來計算多米諾骨牌(粘合在一起的正方形)、多六邊形(正六邊形)和多菱形(等邊三角形)的海施數,他想知道它是否可以適用於多風箏。幸運的是,在滑鐵盧大學本科生艾娃·潘的幫助下,我在前一年添加了對風箏的支援。
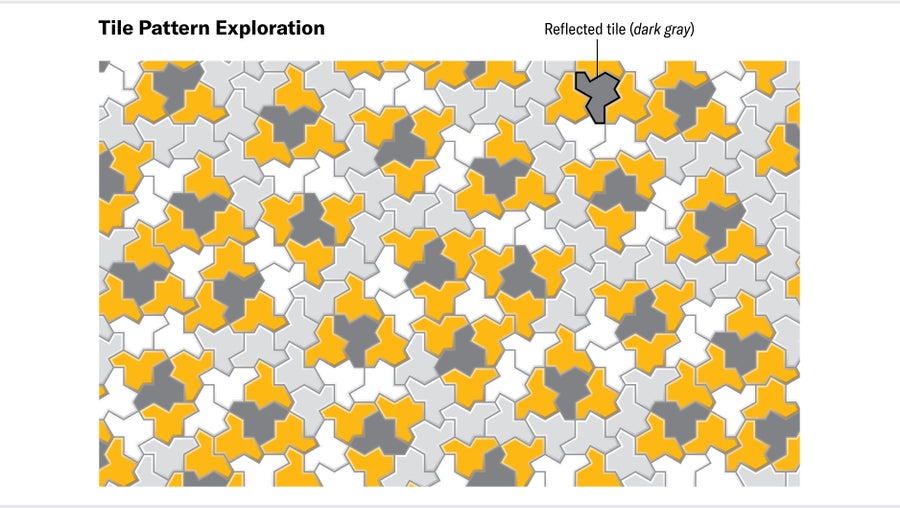
我的軟體輕鬆生成了大量的帽子簇,而沒有卡住,這加強了我們關於帽子平鋪平面的信念。更好的是,這些新的計算機生成的簇成為了原始資料,史密斯和我可以研究這些資料以完善我們的直覺。我們開始以不同的方式對帽子進行分組,通常在數字插圖中手動為它們著色,以尋找秩序。重複出現的模式立即跳了出來,圍繞著嵌入在更大的未反射帽子區域中的稀疏排列的反射帽子(史密斯在他的紙質實驗中也觀察到了這一點)組織起來。
圖片來源:珍·克里斯蒂安森
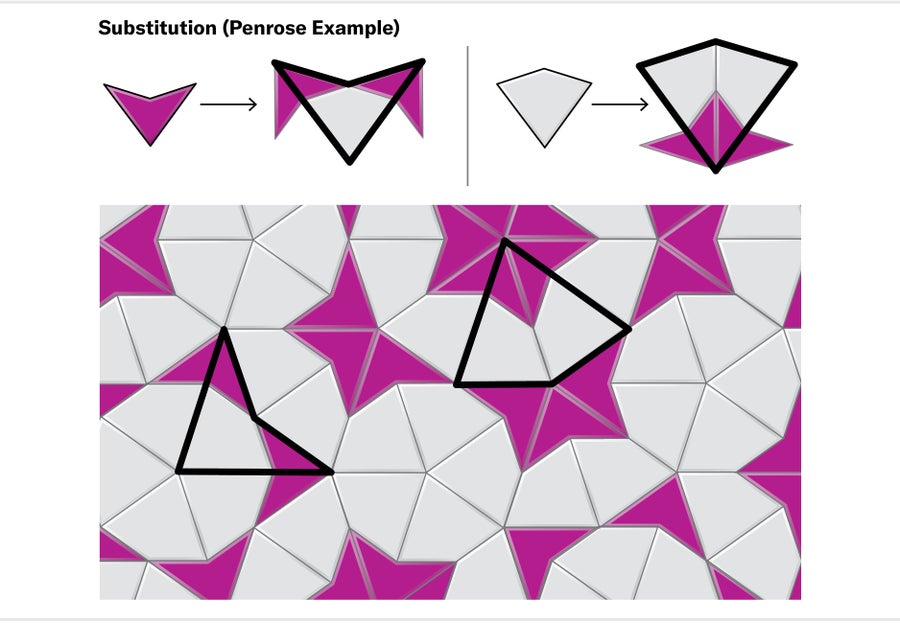
然而,這些模式從未形成平移單元。此外,瓦片似乎以多尺度的相關“圖案”族的形式構建起來。這種重複出現的層次結構暗示了最終證明帽子是非週期性的最佳情況:我們可以希望找到所謂的替換規則系統。在替換系統中,集合中的每個瓦片形狀都配備了一個規則,該規則可以應用於將其替換為瓦片較小副本的集合。有了合適的帽子替換系統,我們或許可以從瓦片的“種子”配置開始,並迭代地應用規則,在進行過程中放大以保持比例。透過這種方式,我們將定義一系列越來越大的帽子簇,這些帽子簇最終將填充整個平面。許多非週期性瓦片集合,包括彭羅斯的集合,都可以證明可以用像這樣的替換系統來平鋪平面。
圖片來源:珍·克里斯蒂安森
在我50歲生日那天,大約在我第一次看到帽子兩週後,我找到了一套初步的替換規則。訣竅是避免直接處理“裸露的”或單個的反射帽子,它們必然表現得與未反射的對應物不同。相反,我將每個反射帽子與其三個鄰居分組在一起,形成一個不可分割的單元,一個新的“元瓦片”,可以將其視為具有自身替換規則的成熟瓦片形狀。我在2022年的剩餘時間裡完善了元瓦片及其規則,最終得到了一個由四個元瓦片組成的系統,每個元瓦片都是小型帽子簇的示意性表示。

圖片來源:珍·克里斯蒂安森
到2023年初,史密斯和我已經完成了一半的非週期性證明,並且可以說這是容易的一半。我們的元瓦片和替換規則保證了帽子是一個單瓦片:它平鋪了無限平面,而不是意外地以一個大的但有限的海施數逐漸消失。而且很容易看出,規則生成的平鋪是非週期性的。但請記住,非週期性與非週期性相去甚遠。也許我們的規則只是構建帽子平鋪的一種過於複雜的方式,並且也存在週期性平鋪。為了完成證明,我們必須證明帽子的每一種平鋪都必然是非週期性的。我對這一步可能會如何發展有一些瞭解,但我的感覺就像我猜想史密斯在前年11月的感覺一樣:接近我的數學專業知識的極限。是時候請求增援了。
2023年1月初,史密斯和我聯絡了古德曼-施特勞斯,一位數學家,他發表了許多關於平鋪理論的重要文章。我認為他是當代研究的權威。他還以數學傳播者和動手活動組織者的身份而聞名,當時他正在過渡到紐約市國家數學博物館的推廣數學家的新角色。換句話說,他已經忙得不可開交了。但他提供了寶貴的意見,並堅持我們立即聯絡邁爾斯。邁爾斯在獲得數學領域組合學的博士學位後離開了學術界,但他仍然對平鋪感興趣。特別是,他維護了一個長期專案,以編目多形體的平鋪屬性。早在2006年,我就為他運行了一些支援計算,並且我正在使用他的軟體作為我自己的海施數研究的一部分。
我以前沒有與邁爾斯進行過如此密切的合作,所以我對他的思維能力、編碼技能和該領域的知識結合感到措手不及。他之前在平鋪方面的工作使他為這一刻做好了充分的準備。僅僅在被介紹到我們正在進行的工作八天後,邁爾斯就完成了證明,並在1月下旬確認帽子是世界上第一個非週期性單瓦片。
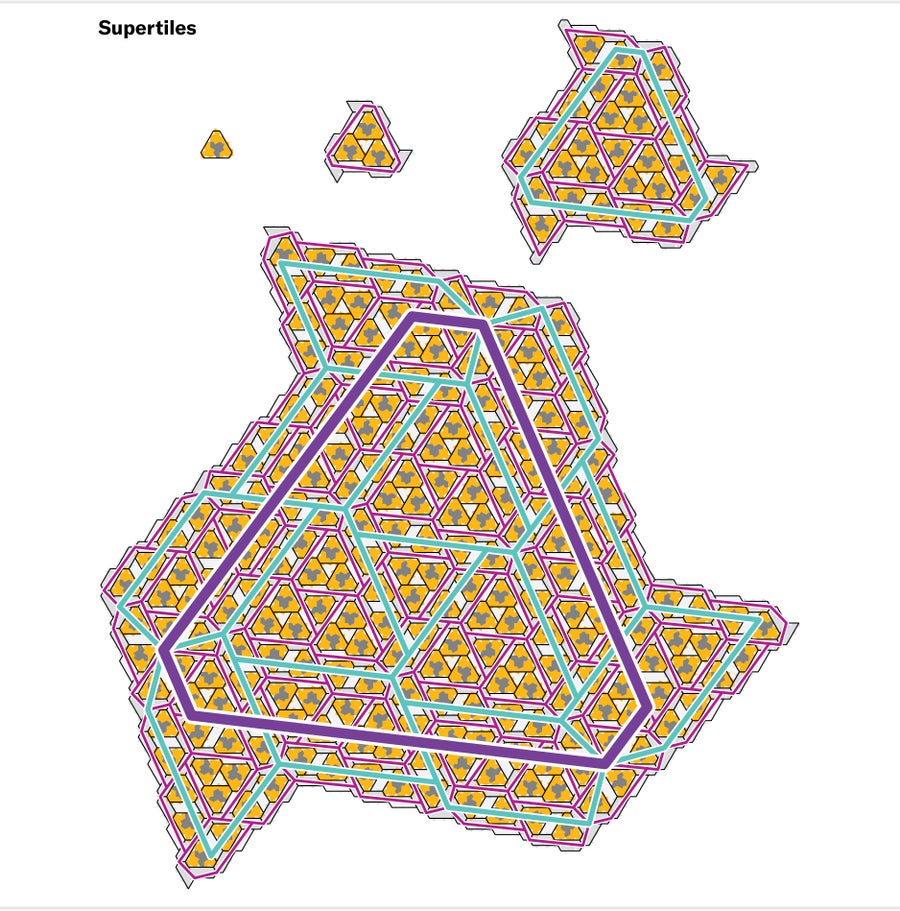
在邁爾斯加入之前,我們已經有了我們的替換規則,並且可以生成平鋪;他的任務是證明帽子的所有平鋪都必須是非週期性的。在非週期性劇本中,此時的標準步驟是證明任何平鋪都帶有替換規則的印記。換句話說,他需要證明對於任何任意的帽子平鋪,都有一種獨特的方式將瓦片分組為元瓦片,將元瓦片分組為超瓦片,依此類推,永遠反向工程一個以完整、無限平鋪結束的無限替換塔。然後,一個預先存在的數學論證將使我們得出結論,即平鋪必須是非週期性的。這種策略的挑戰是在任意帽子平鋪之上找到這個塔,而帽子平鋪的構造在開始時並未被限制為遵守我們的規則。
邁爾斯開發了一種計算機輔助方法來解決這個問題。我們生成了一個詳盡的188個小瓦片簇列表,這些瓦片簇可能出現在帽子平鋪中。這些簇代表圍繞單個帽子的每一種合法排列,以便任何可想象的平鋪中的每個瓦片都必須位於這樣一個簇的中心。然後,邁爾斯證明了這些簇中的每一個都可以以獨特的方式劃分為元瓦片的碎片,這意味著任何平鋪中的帽子都可以分組以產生元瓦片平鋪。最後,他證明,在由元瓦片製成的平鋪中,總是可以將元瓦片分組為更大的簇,稱為超瓦片,這些超瓦片的行為與更大的元瓦片完全相同。最後一步啟動了一種遞迴:因為超瓦片的行為與元瓦片完全相同,所以相同的分組過程也適用於它們。一旦我們將帽子分組為元瓦片,並將元瓦片分組為超瓦片,層次結構的所有後續級別都將透過一個數學技巧鎖定到位。
圖片來源:珍·克里斯蒂安森
我們獲得了我們的獎品,並在2023年2月初開始撰寫一份手稿,與世界分享帽子。如果不是史密斯的數學發現能力,這可能已經是一個神奇故事的結尾。早在2022年12月,他就透過電子郵件給我傳送了第二個形狀,我們稱之為海龜的多風箏,它的行為很像帽子。海龜也散發出一種神秘的非週期性光環。難道史密斯在其他人徒勞地尋找了50年後,在兩週內發現了兩個革命性的形狀嗎?我懇求耐心;可以這麼說,我的腦子裡已經裝滿了帽子。
圖片來源:珍·克里斯蒂安森
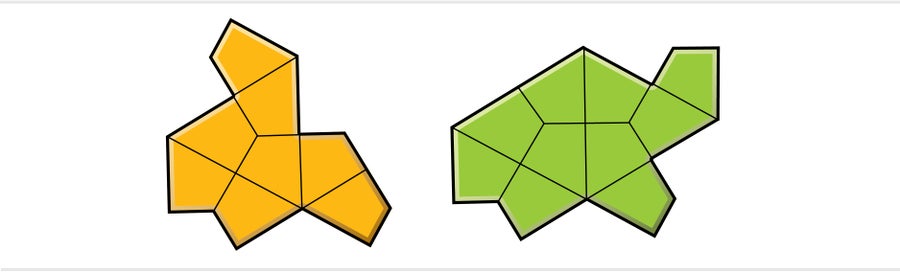
但是在解決了帽子的狀態之後,邁爾斯開始思考被忽視的海龜。一兩週後,他以一個觀察結果震驚了我們三個人,即海龜也必然是非週期性的,因為它實際上只是偽裝成帽子的形狀。事實上,帽子和海龜是連續多邊形家族中的兩個形狀,它們都是非週期性的,並且以相同的方式平鋪。

圖片來源:珍·克里斯蒂安森
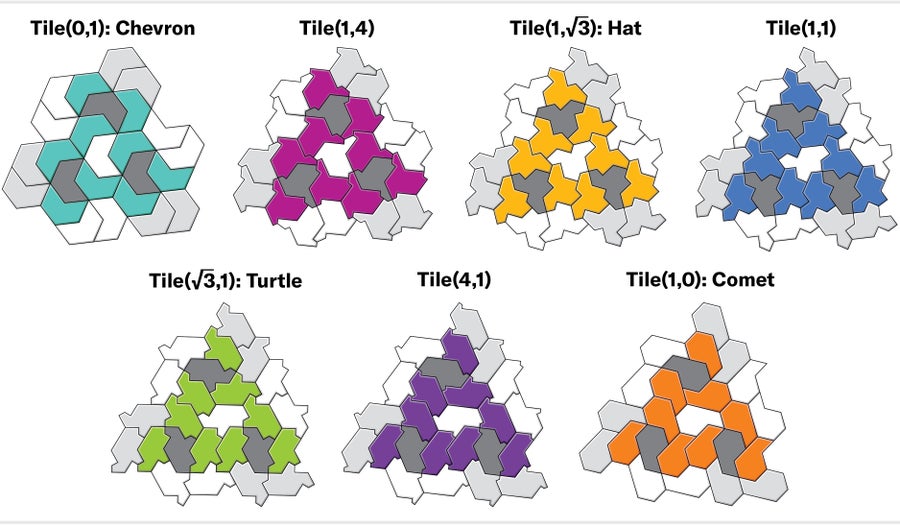
帽子可以被視為邊長為 1 和 √3 的多邊形(其中兩個連續的邊長為 1 的邊形成一個更長的邊)。正如人們可以透過獨立改變矩形水平邊和垂直邊的長度來構造矩形族一樣,我們可以選擇任意兩個數字a和b來替換帽子的邊長,並獲得一個新的多邊形,我們將其稱為瓦片(a,b)。使用此符號,帽子是瓦片(1,√3 ),海龜是瓦片(√3 ,1)。邁爾斯表明,幾乎所有瓦片(a,b)形式的形狀都是非週期性單瓦片,具有相同的平鋪。只有三個例外:瓦片(0,1)(“人字形”)、瓦片(1,0)(“彗星”)和等邊多邊形瓦片(1,1)(從未獲得朗朗上口的暱稱)。這三種形狀都更靈活,既允許週期性平鋪,也允許非週期性平鋪。
圖片來源:珍·克里斯蒂安森
不久之後,邁爾斯加倍強調了他建立的帽子和海龜之間的聯絡,基於瓦片(a,b)連續統,開發了帽子非週期性的第二個顯著證明。他依賴於反證法的經典技術:他假設存在帽子的週期性平鋪,然後,從這種平鋪的存在中,他得出了一個荒謬的結論,表明最初的假設(週期性帽子平鋪)是不可能的。具體來說,他發現可以拉伸和擠壓週期性帽子平鋪中的邊緣,以獲得等效的、週期性的人字形和平鋪。但是人字形和彗星都是建立在不同尺度的規則三角形平鋪之上的多菱形(等邊三角形的並集)。在一個涉及組合學、幾何學和少量數論的論證中,邁爾斯證明,由於人字形和彗星平鋪起源於同一個假定的週期性帽子平鋪,因此它們的底層三角形平鋪必須透過數學上不可能的比例因子相互關聯。這是證明帽子是非週期性單瓦片的第二種方法。這令人興奮,不僅因為它支援了帽子非週期性的主張,而且因為它代表了該領域全新的證明方法,這可能對未來分析其他瓦片有用。
我們在2023年3月將我們的手稿線上釋出,並收到了數學家和平鋪愛好者的熱情、壓倒性的回應。帽子立即成為藝術家、設計師和謎題創作者的靈感來源(例如,您現在可以在Etsy上購買帽子平鋪套裝)。重要的是要記住,這項工作尚未從同行評審的考驗中脫穎而出,儘管它經受了專家的嚴格審查,幾乎沒有留下任何痕跡。
當我們第一次公開帽子時,人們反對我們工作的某一方面比任何其他方面都更頻繁:使用反射瓦片。正如史密斯和我早些時候發現的那樣,帽子的每個平鋪都必須包括稀疏分佈的反射帽子。從數學上講,這種反對意見並沒有破壞我們的結果:單瓦片的公認定義始終允許將反射作為平鋪中的合法移動。儘管如此,許多人想知道,是否有可能存在一種形狀,可以產生“單手”或“手性”非週期性平鋪,其中沒有瓦片被翻轉過來?我們的手稿沒有提供對此問題的見解,我們和其他所有人一樣準備好等待很長時間直到問題解決。
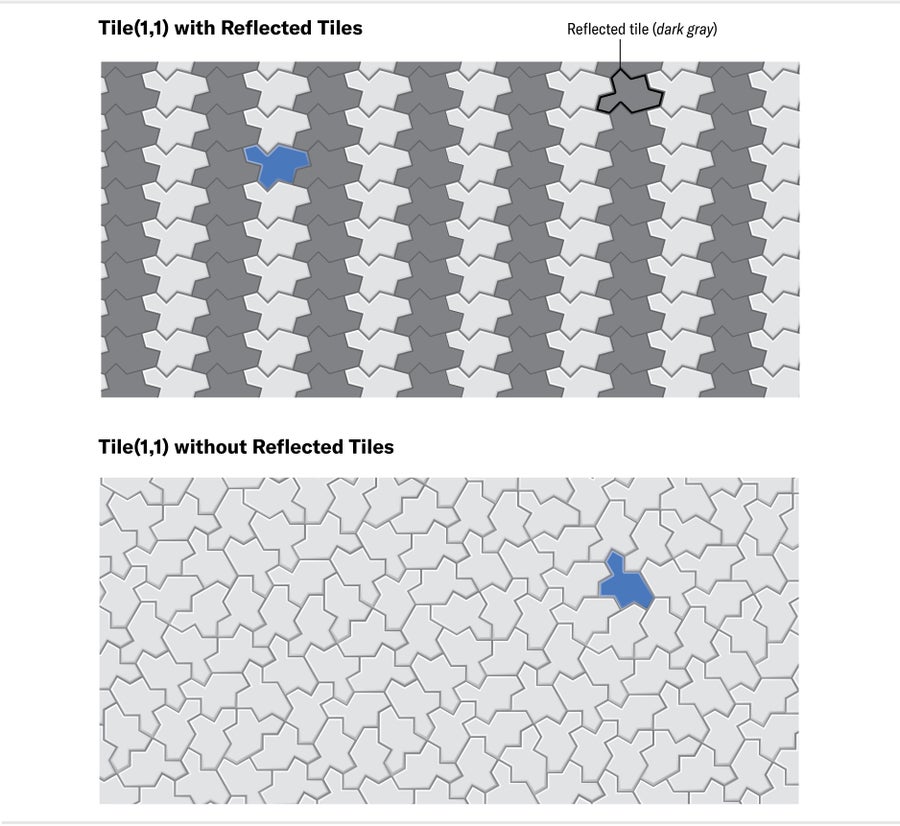
令人高興的是,史密斯又給我們帶來了一個令人震驚的驚喜。在我們第一份手稿釋出不到一週後,他開始透過電子郵件向我們其他人傳送關於瓦片(1,1)的訊息,瓦片(1,1)是包括帽子和海龜在內的連續形狀家族的等邊成員。我們知道這個多邊形不是非週期性的:它允許混合未反射和反射瓦片的週期性平鋪。但是史密斯觀察到,如果他故意將自己限制為單手性瓦片(不允許翻轉),他會產生有趣的瓦片簇。
圖片來源:珍·克里斯蒂安森
我們四個人立即投入到新的合作中。我們計算了瓦片(1,1)未反射副本的大片區域,並研究了它們的模式。我們發現了一種將瓦片分組為重複出現的簇的方法,然後確定了這些簇的替換規則,這些規則產生了具有相同行為的超簇。再一次,這種遞迴分組保證了唯一的無限替換層次結構的存在,該層次結構迫使所有未反射(單手)平鋪都是非週期性的。最後的技巧只是用任意曲線替換瓦片(1,1)的邊緣,這保證了瓦片及其反射不能共存於平鋪中。結果是一個我們稱之為幽靈的形狀家族,所有這些形狀都被證明是手性非週期性單瓦片。
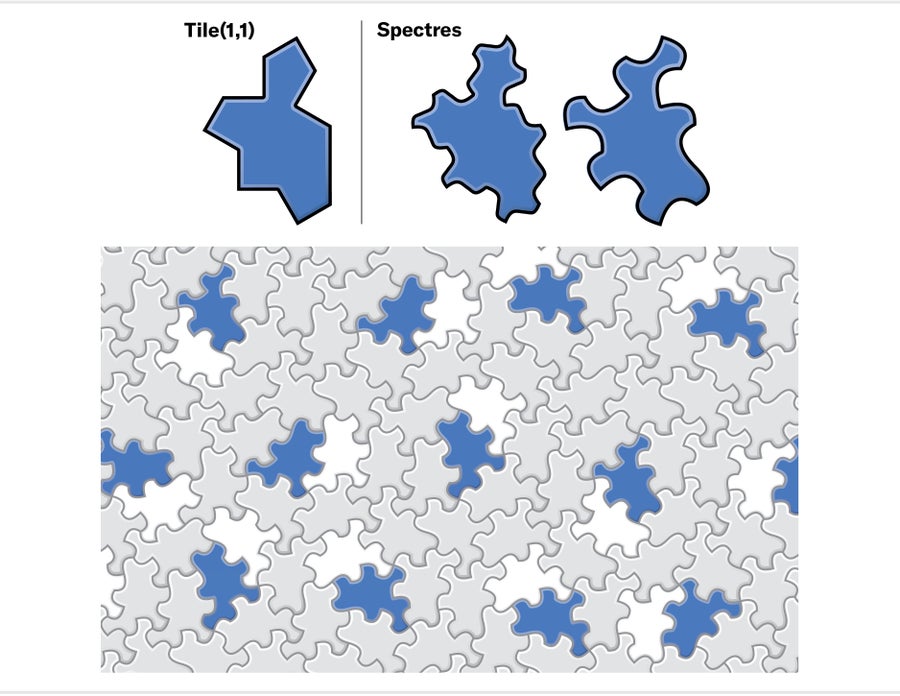
圖片來源:珍·克里斯蒂安森
數學家多年來秘密地研究棘手的問題,最終帶著新的成果出現在陽光下,這其中有一種浪漫色彩。這不是我們的故事。儘管我一直對愛因斯坦問題著迷,但我從未直接研究過它——我只是在2022年11月答案交到我手中時才開始研究。帽子或多或少在史密斯手中成型,我很幸運他選擇聯絡我。幾個月後,我們有了一個完整的證明,這個證明過程據我所知,對我們四個人來說都是輕鬆的。也許我們的速度反映了一個事實,即如果你一開始就擁有正確的形狀,那麼在生成非週期性證明方面有一個清晰的程式可以遵循。我們的輕鬆感也肯定是我們每個人花了數十年思考愛因斯坦問題和相關問題的結果。這種經驗使我們能夠很好地認識到帽子可能是解決方案,並知道該如何處理它。
平鋪理論中不乏未解決的問題,平鋪理論是數學的一個分支,入門門檻低,並且具有很強的視覺吸引力。史密斯加入了一群熱情的業餘愛好者的行列,他們為該領域做出了重要貢獻,通常是在閱讀了本雜誌上的未解決問題之後。他與羅伯特·阿曼並駕齊驅,後者獨立發現了許多與彭羅斯相同的結果,併為平鋪理論貢獻了其他重要的思想;瑪喬麗·賴斯,她發現了新的五邊形單瓦片類別;以及瓊·泰勒,她是索科拉爾-泰勒瓦片的原創者。我還應該包括藝術家M.C.埃舍爾,他發明了繪製他的鑲嵌圖案所需的數學,即使他根本不會認為這是數學。
隨著我們的非週期性單瓦片的影響向外擴散,我相信它將刺激新的學術研究。但我希望我們也吸引其他可能認為數學令人望而生畏,但現在認識到有玩耍機會的人。

圖片來源:米里亞姆·馬丁西克

