可能的最大自然數是多少? 透過使用“自然”這個詞,我已經排除了你簡單地回答無窮大 (∞) 來破壞猜謎遊戲的可能性。但即使我們允許無限大的值,這個回答也會引起問題。那麼 ∞ + 1,∞2 或 ∞∞ 呢? 如果人們提出這些答案來回答最大的自然數問題,誰才是對的?
答案是誰都不對,因為無窮大不是一個普通的數字,它不遵循通常的計算規則。 例如,無論你從 –∞、0 還是 1 開始,數軸都是無限的。 因此,諸如 ∞ + 1 之類的陳述毫無意義。 此外,即使是無限值也存在差異:無窮大並不總是等於無窮大。 因此,無窮大不會是最大數字競賽中有保證的獲勝者。
人類花費了數千年的時間才意識到這個想法並將其鑄造成一個簡潔的理論。 19 世紀末,數學家格奧爾格·康托爾透過思考數量及其大小,為無窮大的數學概念奠定了基礎。 例如,{1, 2, 3, 4} 和 {x, y, z, q} 都由四個元素組成,因此大小為 4,專家稱之為“基數為 4”。
支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。 透過購買訂閱,您將幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。
另一方面,自然數 {0, 1, 2, 3,...} 包含無限多個元素。 我們可以將 1 加到任何自然數上; 結果也是一個自然數。 如果我們現在看一下所有偶數的集合 {0, 2, 4,...},我們可能會認為它只有一半大小——畢竟,只有每隔一個自然數才包含在其中。 但康托爾認識到,這兩個集合(自然數和偶數)具有相同的基數。
匹配集合和可數無窮大
正如我在另一篇專欄文章中討論的那樣,當康托爾比較兩個集合的元素時,他得出了這個令人驚訝的結果。 如果你想知道集合 A(例如,公交車站的人)是否與另一個集合 B(公交車上的空座位)完全一樣大,你可以為 A 中的每個元素分配一個來自 B 的元素。 如果最後還有人站著,那麼 A 比 B 大。 另一方面,如果還有空座位,那麼 B 必須比 A 大。
但是,如果你可以為每個人精確地分配一個座位,那麼這兩個集合的大小完全相同,因此具有相同的基數。 透過這種方式,康托爾還研究了無限集合的基數。 例如,你可以將任何自然數精確地對映到一個偶數,例如,透過形成對 (0,0)、(1,2)、(2,4)、(3,6)、...、(n, 2n)。 對映完全有效。 最後既沒有留下自然數,也沒有留下偶數。 因此,這兩個集合包含相同數量的元素。
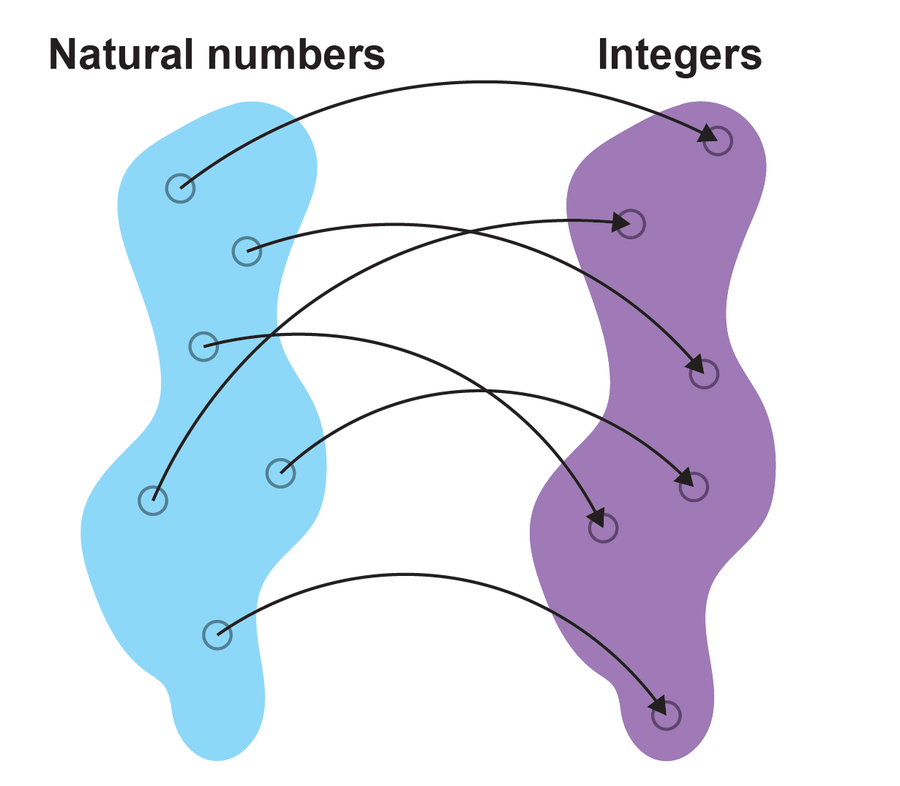
如果兩個集合之間存在一對一的對映,則這兩個集合相等。 信用:Spektrum der Wissenschaft/Manon Bischoff,大眾科學風格
這裡出現了一個重要的教訓。 當涉及到無窮大時,不要憑直覺行事。 這些想法很少是直觀的。
不僅自然數和偶數的基數相同,對映兩個集合的技巧也可以應用於其他例子。 例如,所有奇數的集合與所有自然數的集合大小相同——所有整數(包括負值)、素數甚至有理數(包括分數)的集合也是如此。 對於這些集合中的每一個,都存在一個對映,該對映將自然數 {1, 2, 3,...} 唯一地分配給每個元素。 這意味著你可以——至少在理論上——為這些集合的元素編號(如果你有無限的時間和空閒)。
最小的無窮大因此得名。 自然數的基數稱為“可數無窮大”,用 ℵ0 (讀作“阿列夫零”)表示。 因此,與其在最大數字競賽中提交答案“無窮大”,不如提供 ℵ0。
到目前為止提出的集合都具有相同的基數。 但實數打破了這個模式。 如果除了有理數之外,你還允許無理數值,例如 2 的平方根、pi 或 蔡廷常數,那麼集合突然變得如此之大,以至於你無法再列舉它的元素——即使列表是無限長的。
實數的無窮大超過了自然數
康托爾用他的第二個“對角論證”證明了這個事實。 這是一種反證法:你從假設存在可數無窮多個實數開始,並從這個想法中推匯出一個矛盾的陳述(即,“不可能存在可數無窮多個實數”)。
為了繼續,你不必考慮所有實數。 假設 0 到 1 之間的所有實數值都是可數的就足夠了(我們很快就會看到,這是錯誤的)。
因此,你可以將所有這些值寫在一個無限長的列表中,一個在另一個下面。 例如
0.32476834567854765 ...
0.84737834527845745 ...
0.78347864586745768 ...
0.78347863763547879 ...
...
列表的排序方式無關緊要。 唯一重要的是它是完整的。 如果我們真的可以數出所有的值,那麼我們的列表必須包含 0 到 1 之間的每個實數。 但康托爾證明了他可以構造另一個介於 0 和 1 之間的數字,該數字不會出現在列表中。
他是這樣做的:新數字的第一位小數對應於列表中第一個數字的第一位小數加一——即上例中的 4。 第二位小數是透過計算第二個數字的第二位小數加一得到的——即 5。 對於第三位,你將第三個數字的第三位小數加 1,依此類推。 (如果你遇到 9,你可以將值更改為 0。)
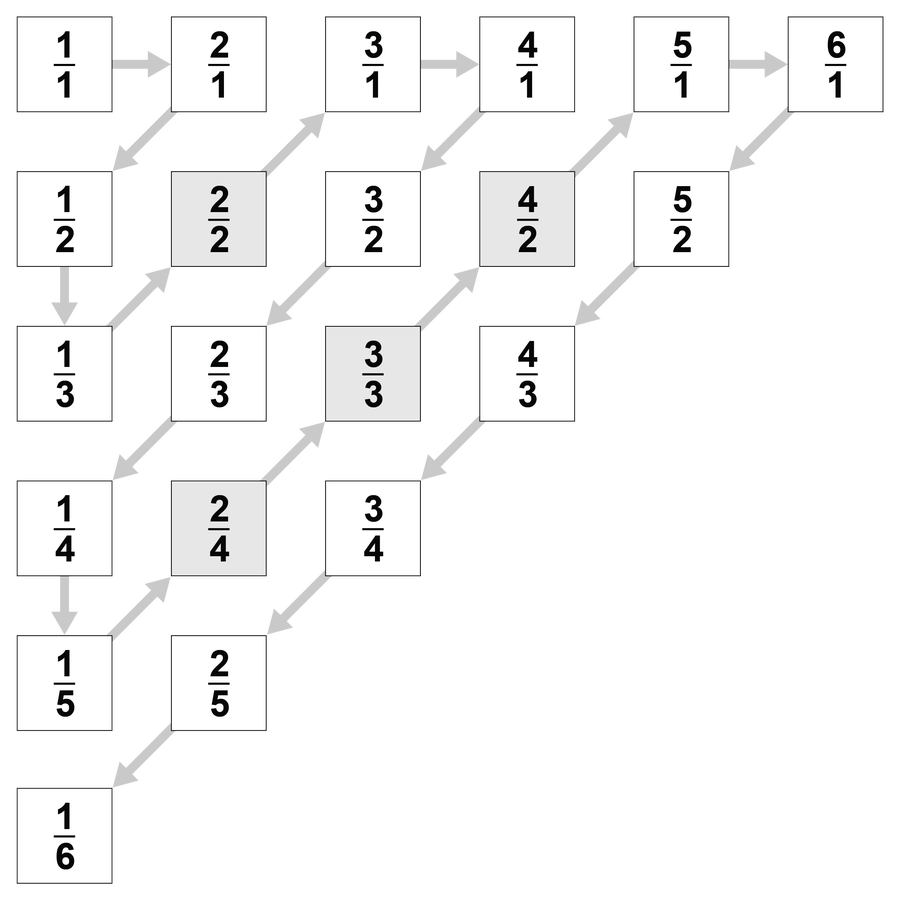
要建立康托爾的對角論證,你可以首先透過遵循箭頭並忽略分子大於分母的分數來建立所有有理數的列表。 信用:Buckyball Design; 來源 維基百科
透過這種方式,將獲得一個具有無限位小數的無理數。 它不出現在列表中,因為它總是與列表中列出的每個數字至少在一個數字上不同。 因此,列表不可能完整,這與最初的假設相矛盾。 因此,康托爾可以得出結論,存在“不可數”的實數。
一個可證明不可證明的假設
除了自然數的基數 ℵ0 之外,至少還有一個(不可數)無窮大——它可能比 ℵ0 更適合在尋找最大數字的競賽中獲勝。
實數集究竟有多大? 康托爾在調查是否存在一個數字集合,其大小大於自然數但小於實數時,也問了自己同樣的問題。 在沒有找到這樣的集合後,這位數學家在 1878 年提出了他著名的“連續統假設”。 它指出,不存在基數介於自然數和實數之間的集合。
但康托爾無法證明他的假設——任何其他人也無法證明。 事實證明,連續統假設屬於我們基本數學框架無法解決的陳述。 它們是可證明不可證明的:你既不能透過通常的數學手段證明也不能證偽這個猜想。 (庫爾特·哥德爾證明了在 1931 年,在數學的每個有意義的表述中都存在這種不完備性。)
換句話說,你可以假設連續統假設為真,並且永遠不會遇到矛盾。 然而,反過來,你可以假設在自然數和實數的基數之間存在其他無窮大——並且也不會遇到任何問題。 這對於數學家來說並不是特別令人滿意。 畢竟,我們討論的是實數的大小——沒有人知道存在多少個這樣的值。 作為回應,有些人正試圖擴充套件該學科的基本框架,以便從這個更大的理論中推匯出一個工具來證明或證偽連續統假設。
專家們在這個努力上絕非意見一致。 數學的基礎——“策梅洛-弗蘭克爾集合論”——由九個未經證明的基本陳述(所謂的公理)組成,這些公理構成了整個學科的基礎。 花費了幾次嘗試才找到適合該任務的公理集,因為它必須滿足幾個要求。 該集合應儘可能少地包含公理,並且它們應直觀地為真且不太複雜。 其他示例是空集公理,它宣告存在一個沒有元素的集合,以及配對公理,根據該公理,具有相同元素的兩個集合是相等的。
策梅洛-弗蘭克爾集合論的九個公理(連同選擇公理)足以構建我們所知道的數學。 但連續統假設避開了它們。 為了更詳細地研究實數的基數,你必須擴充套件當前的集合論以包含其他基本陳述。 例如,你可以將陳述“連續統假設為真”附加到公理組中。 然而,這不會是一個好的公理。 與其他陳述不同,並不直接清楚為什麼這個陳述應該是真的。
因此,專家們正在尋找其他直觀上為真並且可以用來研究連續統假設的公理。 已經有一些有希望的候選者——有些會證實康托爾的猜想,而另一些會反駁它。 哪種擴充套件版本的集合論會佔上風(如果有的話),仍有待觀察。 只要情況如此,實數有多少個仍然是一個未解之謎。
即使這仍然是一個謎,但早已知道存在基數比實數集大得多的集合——即使實數本身是無限的。 如果你想贏得最大數字遊戲,你應該去追逐最大的無窮大。
本文最初發表在《光譜》雜誌上,並經許可轉載。
