無窮範疇論提供了數學的鳥瞰視角

在一個清爽的新英格蘭秋日，我大學三年級的時候，走過一個地鐵入口，一個數學問題吸引了我的眼球。一個男人站在他潦草地寫在牆上的幾個腦筋急轉彎旁邊，其中一個問題是用虛構的直尺和圓規構造一個體積是給定立方體兩倍的立方體。

這讓我停下了腳步。我以前見過這個問題。事實上，這個挑戰已經有兩千多年的歷史了，據普魯塔克所說，它歸功於柏拉圖。直尺可以用來在任何方向上延長線段，圓規可以用來以選定的中心畫出任意半徑的圓。這個特殊難題的癥結在於，最終繪圖中出現的任何點或長度都必須是在開始時就存在的，或者可以從先前提供的資訊中構造出來。

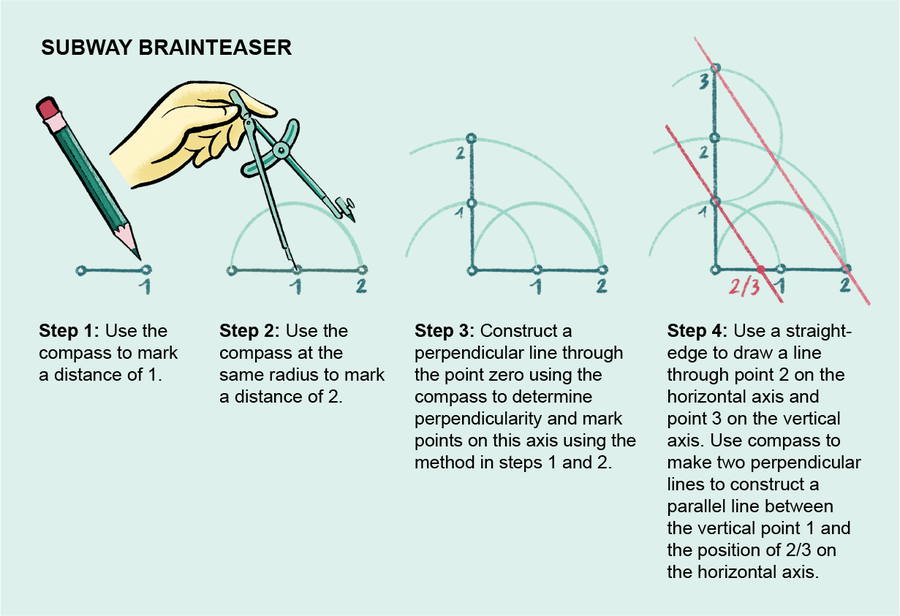
要將立方體的體積翻倍，你需要從它的邊長開始。這裡這個值不妨設為 1，因為它是唯一給出的測量單位。為了構造更大的立方體，你必須想辦法畫出它的邊，使其具有新的所需長度，即 ∛2（2 的立方根），僅使用直尺和圓規作為工具。

支援科學新聞業

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱，您將幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。

這是一個難題。2000 多年來，沒有人成功解決它。最終，在 1837 年，皮埃爾·洛朗·萬策爾解釋了為什麼沒有人成功，他證明了這是不可能的。他的證明使用了當時最前沿的數學，其基礎是由他同時代的法國人埃瓦里斯特·伽羅瓦奠定的，伽羅瓦在 20 歲時死於一場決鬥，這場決鬥可能與一段不幸的戀情有關。在我自己 20 歲的黃金年齡，我取得的數學成就遠不及他，但我至少理解了萬策爾的證明。

這是這個想法：給定一個點作為原點和一個長度為 1 的距離，相對容易地使用直尺和圓規來構造數軸上的所有點，這些點的座標是有理數（像數學家通常做的那樣，忽略在有限時間內實際繪製無限多個點的不可能性）。

萬策爾證明，如果只使用這些工具，則每個新構造的點都必須是二次多項式方程 ax² + bx + c = 0 的解，其係數 a、b 和 c 是先前構造的點之一。相比之下，點 ∛2 是三次多項式 x³ − 2 = 0 的解，而伽羅瓦的“域擴張”理論明確地證明，你永遠無法透過解二次方程來獲得不可約三次多項式的解，本質上是因為 2 的任何冪都不能整除數字 3。

有了這些事實，我就忍不住要與街上的那個人交談。可以預見的是，我試圖解釋我如何知道他的問題無法解決的嘗試並沒有真正取得任何進展。相反，他聲稱我的教育讓我思想封閉，無法“跳出框框思考”。最終，我的女朋友設法把我從爭論中解脫出來，我們繼續前行。

但一個有趣的問題仍然存在：我，一個大學三年級仍然乳臭未乾的本科生，是如何在短短幾周內學會自如地操作像伽羅瓦域這樣的抽象數系的？這些材料出現在一門課程的末尾，課程中充滿了對稱群、多項式環和相關的寶藏，這些寶藏會讓像艾薩克·牛頓、戈特弗裡德·萊布尼茨、萊昂哈德·尤拉和卡爾·弗里德里希·高斯這樣的數學巨匠感到震驚。數學家是如何快速地向每一代新的本科生傳授前一代專家感到震驚的發現的？

部分答案與數學的最新發展有關，這些發展透過不斷提高的抽象程度提供了該領域的“鳥瞰視角”。範疇論是數學的一個分支，它解釋了不同的數學物件如何被認為是“相同的”。它的基本定理告訴我們，任何數學物件，無論多麼複雜，都完全由其與相似物件的關係決定。透過範疇論，我們使用廣泛適用於整個數學範疇的通用規則，而不是深入研究僅適用於單個領域的個別定律，來向年輕的數學家傳授最新的思想。

隨著數學的不斷發展，數學家們對何時兩個事物“相同”的意識也在擴充套件。在過去的幾十年裡，許多其他研究人員和我一直在研究範疇論的擴充套件，以理解這種新的擴充套件的唯一性概念。這些新的範疇，稱為無窮範疇（∞-範疇），將範疇論擴充套件到無限維度。∞-範疇的語言為數學家提供了強大的工具來研究物件之間的關係過於微妙而無法在傳統範疇中定義的問題。“放大到無窮”的視角提供了一種思考舊概念的新穎方式，以及發現新概念的途徑。

範疇

像我認識的許多其他數學家一樣，我被這個學科吸引，部分原因是我的記憶力差。這讓許多人感到困惑，他們記得高中數學充滿了需要記憶的公式——三角恆等式就是其中之一。但令我欣慰的是，最常用的公式可以從 sin²θ + cos²θ = 1 重新推匯出來，而後者本身就有一個優雅的幾何解釋：它是勾股定理在斜邊長為 1，銳角為 θ 度的直角三角形中的應用。

數學的這種烏托邦式的願景，即一切都“有道理”，沒有什麼需要記憶，在大學層面在某種程度上瓦解了。在那個時候，學生們開始瞭解過去幾個世紀裡被設想出來的數學物件動物園。“群”、“環”和“域”屬於數學的一個領域，稱為代數，這個詞來源於九世紀波斯數學家和天文學家穆罕默德·伊本·穆薩·花剌子米的一本書，這本書的標題有時被翻譯為《還原與平衡的科學》。在接下來的千年裡，代數從研究多項式方程解的性質演變為研究抽象數系。由於沒有實數 x 滿足方程 x² + 1 = 0，數學家們透過新增一個虛數 i 並強制規定 i² + 1= 0，構建了一個新的數系——現在稱為複數。

代數只是數學本科課程中的科目之一。其他基石包括拓撲學——對空間的抽象研究——和分析學，它從對實函式微積分的嚴格處理開始，然後分支到機率空間和隨機變數以及複流形和全純函式的更奇特的領域。學生應該如何理解這一切呢？

數學中一個自相矛盾的想法是透過抽象來簡化。正如歐金妮亞·鄭在《非理性世界的邏輯藝術》中所說，“抽象的一個強大之處在於，當您忘記一些細節時，許多不同的情況會變得相同。”現代代數是在 20 世紀初建立的，當時數學家們決定統一他們對在考慮多項式方程的解或平面圖形的配置中出現的許多代數結構示例的研究。為了連線對這些結構的研究，研究人員確定了描述其共同屬性的“公理”。群、環和域被引入數學世界，以及數學物件可以用其擁有的屬性來描述並“抽象地”探索的思想，獨立於特定示例或構造的支架。

約翰·霍頓·康威曾著名地思考過數學事物的好奇本體論：“毫無疑問它們確實存在，但你無法戳和戳它們，除非透過思考它們。這非常令人驚訝，儘管我一生都是數學家，但我仍然不明白。事物怎麼能在那裡而不實際存在呢？”

但是，這個數學物件的世界可以在不實際存在的情況下存在，這造成了一個問題：這樣的世界太大了，任何人都無法理解。即使在代數內部，也有太多數學事物需要研究，以至於沒有時間理解所有事物。大約在 20 世紀之交，數學家們開始研究所謂的泛代數，指的是“集合”，它可以是對稱性的集合、某個系統中的數字或完全其他的東西，以及各種運算——例如，加法和乘法——滿足相關公理列表，例如結合律、交換律或分配律。透過做出不同的選擇——運算是部分定義的還是完全定義的？它是可逆的嗎？——人們可以得到標準的代數結構：群、環和域。但該學科不受這些選擇的約束，這些選擇僅代表無限可能性陣列中極小的一部分。

新的抽象數學物件的激增帶來了自身的複雜性。簡化的一種方法是引入更深層次的抽象，令人驚訝的是，我們可以同時證明關於各種數學物件的定理，而無需明確說明我們正在談論哪種物件。

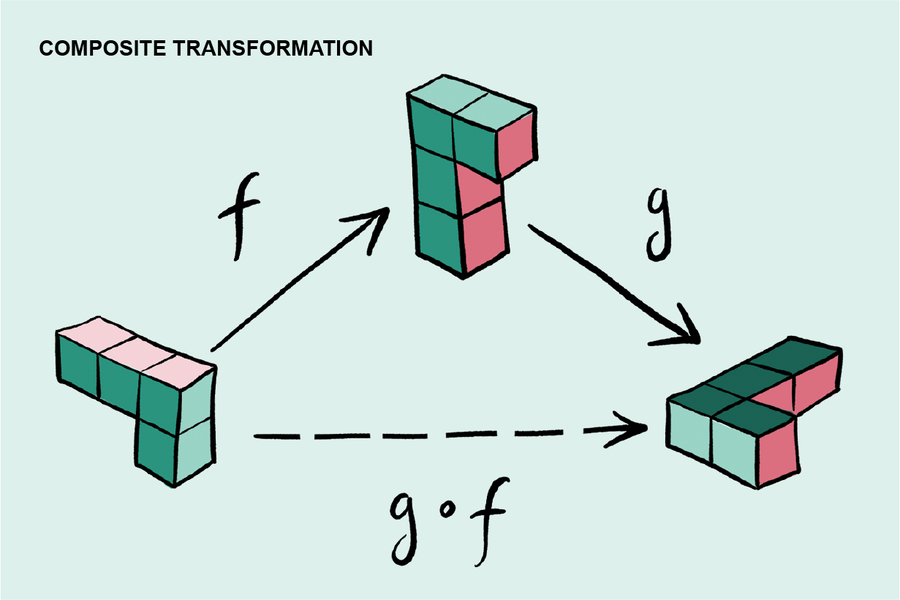
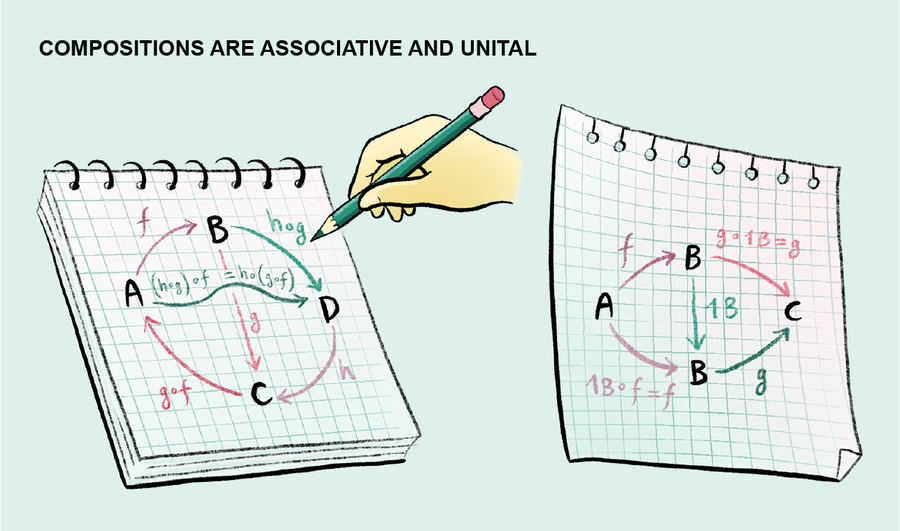
範疇論是由塞繆爾·艾倫伯格和桑德斯·麥克萊恩在 20 世紀 40 年代建立的，它正是這樣做的。儘管它最初是為了嚴格定義口語術語“自然等價”而引入的，但它也提供了一種普遍思考泛代數和數學其他領域的方式。藉助艾倫伯格和麥克萊恩的語言，我們現在可以理解，每種數學物件都屬於它自己的範疇，這是一個指定的物件集合，以及一組描繪為物件之間箭頭的變換。例如，線上性代數中，人們研究抽象向量空間，例如三維歐幾里得空間。在這種情況下，相應的變換稱為線性變換，並且每個變換都必須具有指定的源和目標向量空間，指示哪些型別的向量作為輸入和輸出出現。與函式一樣，範疇中的變換可以“組合”，這意味著您可以將一個變換應用於另一個變換的結果。對於任何一對變換 f: A → B （讀作“f 是從 A 到 B 的變換”）和 g: B → C，範疇指定一個唯一的複合變換，寫為 g ∘ f: A → C （讀作“g 複合 f 是從 A 到 C 的變換”）。最後，這個組合律是結合律的，這意味著 h ∘ (g ∘ f) = (h ∘ g) ∘ f。它也是單位的：每個物件 B 都有一個“單位變換”，通常用 1_B 表示，其屬性是對於任何變換 g 和 f ，只要它們的源和目標分別等於 B，則 g ∘ 1_B = g 且 1_B ∘ f = f。

範疇如何幫助面對太多數學物件而沒有足夠時間學習所有這些物件的倒黴的本科生？您可以在泛代數中定義的任何結構類都可能與其他所有結構類不同，但這些物件所在的範疇在可以透過範疇語言精確表達的方式上非常相似。

憑藉足夠的經驗，數學家可以知道當他們遇到一種新的代數結構時會發生什麼。這個想法反映在現代教科書中，這些教科書按系列發展群、環和向量空間的理論，本質上是因為這些理論是平行的。在這些範疇與學生在拓撲學或分析學課程中遇到的範疇之間存在其他更鬆散的類比，這些相似之處使他們能夠更快地吸收新材料。這種模式使學生能夠花費更多時間探索區分各個數學子學科的特殊主題——儘管數學研究的進展通常受到先前不相關的領域之間新的和令人驚訝的類比的啟發。

對稱性

從具體的數學結構到公理系統，再到屬於範疇的一般物件，層層遞進的抽象級別提出了一個新的挑戰：說一個事物與另一個事物“相同”不再非常清楚是什麼意思。例如，考慮一個群，在數學中，群是對稱性的抽象集合，芝加哥大學的艾米·威爾金森喜歡將群的元素描述為“移動”，這些移動翻轉或旋轉一個物體，然後將其放置到類似於原始位置的位置。

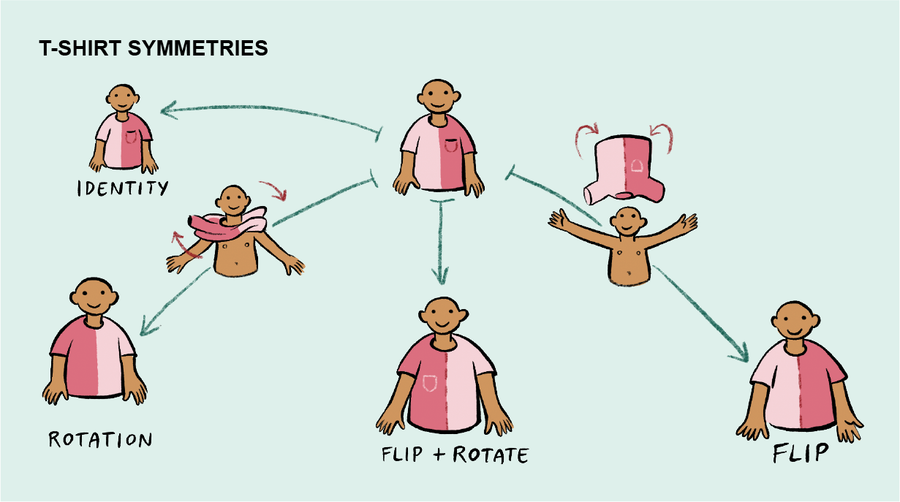
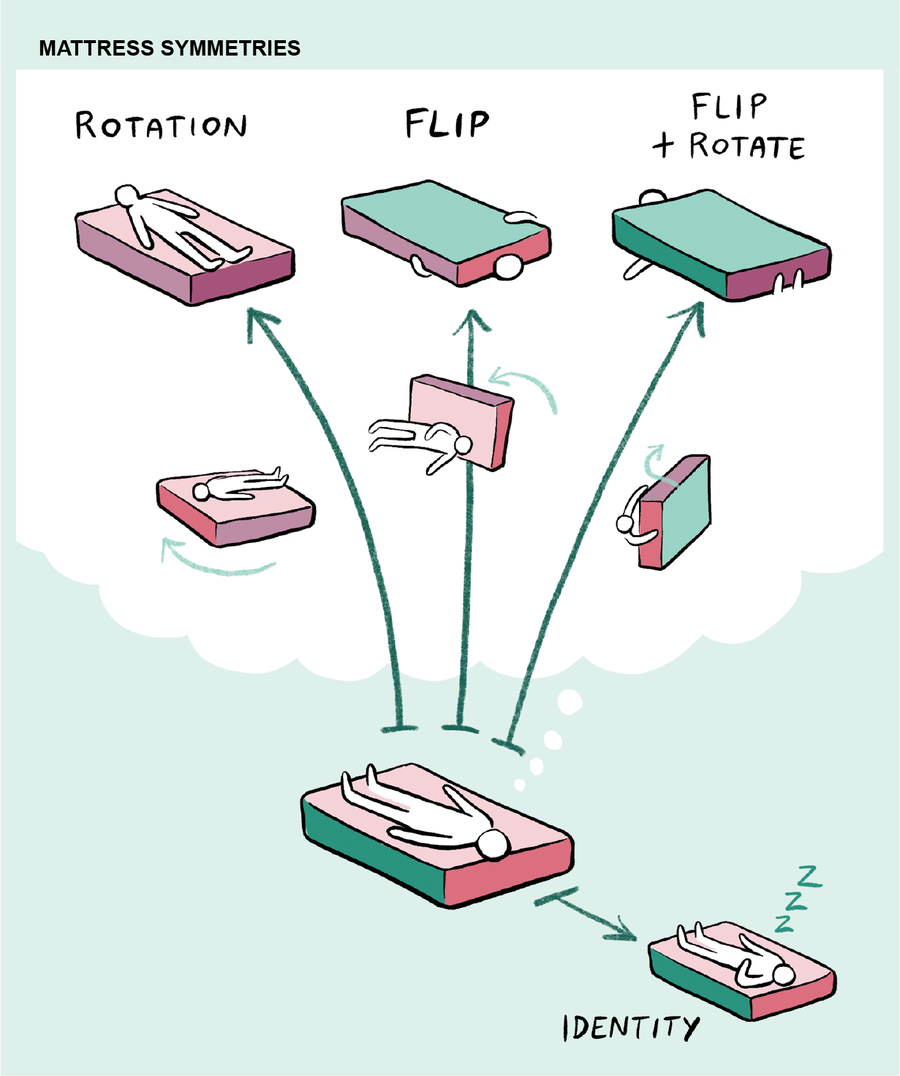
例如，我們可以探索 T 恤的對稱性。一種對稱性可以被認為是“恆等移動”，即一個人只是像通常那樣穿著 T 恤。另一種對稱性對應於這樣的移動，即穿著者將手臂從袖孔中取出，並在 T 恤仍然繞在脖子上的情況下，將襯衫旋轉 180 度，將手臂放入相對的孔中：T 恤仍然正面朝外，但現在是反向穿著。另一種對稱性對應於完全脫下 T 恤，將其翻過來，然後以使每隻手臂都穿過其最初所在的孔的方式重新穿上。T 恤現在是裡外翻轉且反向穿著。最後的對稱性結合了這兩個移動：與群體的典型情況不同，這些移動可以以任何順序執行，而不會改變最終結果。這些四個移動中的每一個都算作“對稱性”，因為它們導致襯衫的穿著方式與您開始時基本相同。

另一個群是“床墊翻轉群”，它描述了床墊的對稱性。除了恆等移動（當床墊保持在其原始位置時應用）之外，一個人還可以透過上下旋轉床墊、前後翻轉床墊或按順序執行兩個移動來移動床墊。（床墊通常不是正方形的，但如果是正方形的，則會有比此處描述的更多的對稱性。）儘管 T 恤與床墊沒有太多關係，但在某種意義上，這兩個對稱群具有相同的“形狀”。首先，這兩個對稱群都具有相同數量的移動（在這種情況下，為四個），並且至關重要的是，您可以將 T 恤群中的每個移動與床墊翻轉群中的移動配對，以便相應移動的組合也對應。換句話說，您可以匹配來自兩個群的移動（將恆等移動與恆等移動匹配，將翻轉與翻轉匹配，將旋轉與旋轉匹配，依此類推）。其次，如果您從一個群中取出兩個移動並按順序執行它們，則最終位置將與按順序執行來自另一個群的相應移動的最終結果匹配。用技術術語來說，這些群透過“同構”連線，這是一個詞，其詞源——來自希臘語 isos，意為“相等”，以及 morphe,意為“形式”——表明其含義。

我們可以在任何範疇中定義同構的概念，這使我們能夠在數學上下文之間傳遞這個概念。範疇中兩個物件 A 和 B 之間的同構由一對變換給出，f: A → B 和 g: B → A, 其屬性是複合 g ∘ f 和 f ∘ g 等於各自的恆等式 1_A 和 1_B。 在拓撲空間範疇中，同構的範疇概念由一對逆連續函式表示。例如，存在一個連續變形，可以使您將未烘焙的甜甜圈轉換為類似咖啡杯的形狀：甜甜圈孔變成把手，杯子由您用拇指按下的凹陷形成。（為了使變形是連續的，您必須在不撕裂麵糰的情況下進行此操作，這就是為什麼在嘗試實驗之前不應烘焙甜甜圈的原因。）

這個例子啟發了一個笑話，即拓撲學家無法區分咖啡杯和甜甜圈：作為抽象空間，這些物件是相同的。在實踐中，許多拓撲學家可以說比這更不善於觀察，因為通常採用更靈活的約定來處理兩個空間“相同”的情況，識別任何兩個僅僅是“同倫等價”的空間。這個術語指的是更奇特的空間同倫範疇中同構的概念。同倫等價是另一種型別的連續變形，但在這種情況下，您可以識別不同的點。例如，想象一下從一條褲子開始，然後縮小褲腿的長度，直到剩下丁字褲，另一個具有相同基本拓撲結構的“空間”——仍然有兩個腿孔——即使最初的二維服裝已縮小為一維的細繩。

另一個同倫等價透過“反向大爆炸”將三維歐幾里得空間的無限廣闊空間塌縮為一個點，其中每個點都飛回其原點，運動速度隨著距初始大爆炸位置的距離而增加。

我們可以用同構事物相互替代而不會從根本上改變構造或論證性質的直覺是如此強烈，以至於事實上範疇論者重新定義了單詞“the”，使其含義更接近口語英語中的“a”。例如，有一個概念稱為兩個集合 A 和 B 的不交併集。與普通並集類似，不交併集 A ⨆ B 具有 A 的每個元素的副本和 B 的每個元素的副本。但是，與普通並集不同，如果 A 和 B 有一個共同的元素，則不交併集 A ⨆ B 具有該元素的兩個副本，其中一個副本以某種方式記住它來自 A, 而另一個副本以某種方式記住它來自 B。

有許多不同的方法可以使用集合論的公理來構造不交併集，這些方法不會產生完全相同的集合，但必然會產生同構的集合。與其浪費時間爭論哪種構造是最規範的，不如將這種歧義掃到地毯下，並在要考慮滿足所需普遍屬性的任何特定集合時，簡單地提及“the”不交併集。在另一個例子中，數學家將 T 恤對稱群和床墊翻轉群都稱為“克萊因四元群”。

無限維範疇

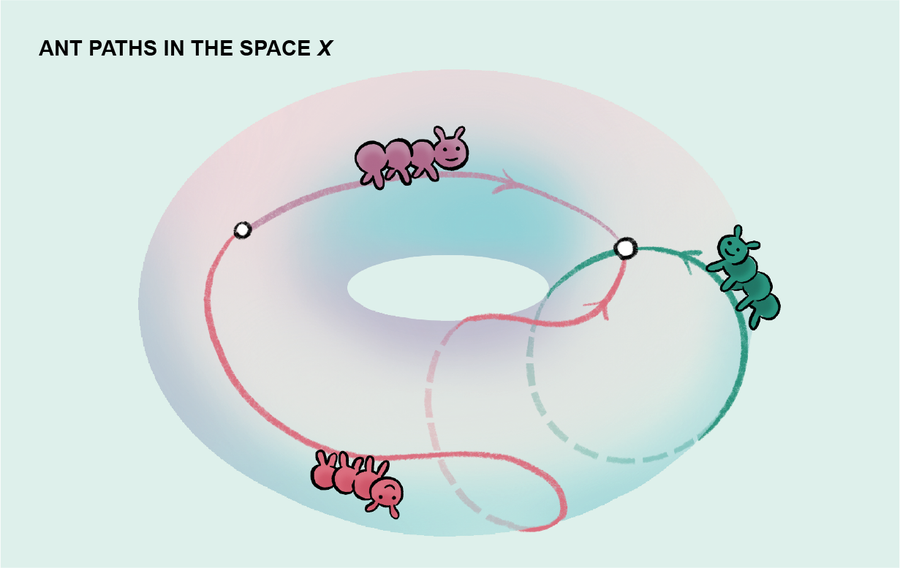
一個關於範疇論基本定理起源的經常被講述的故事是，一位名叫野田信夫的年輕數學家在 1954 年巴黎北站火車站向麥克萊恩描述了一個“引理”，或輔助定理。野田開始在站臺上解釋引理，並在火車離開車站前繼續在火車上解釋。這個引理的結果是，任何範疇中的任何物件都完全由其與其他物件的關係決定，這種關係由從該物件到其他物件或從其他物件到該物件的變換編碼。因此，我們可以透過使用連續函式 f: T → X 映射出其他空間 T 來表徵拓撲空間 X。例如，空間 X 的點對應於連續函式 x: * → X, 其域是具有單點的空間。我們可以透過考慮對映 p: I → X, 來回答空間 X 是連通的還是不連通的問題，其域是區間 I = [0,1]。每個這樣的對映都定義了空間 X 中從點 p(0) 到點 p(1) 的引數化“路徑”，可以將其視為螞蟻在空間 X 周圍走動時可能採取的軌跡。

我們可以使用空間的點和路徑將拓撲學問題轉化為代數問題：每個拓撲空間 X 都有一個關聯的範疇 π₁X，稱為 X 的“基本群胚”。此範疇的物件是空間的點，變換是路徑。如果一條路徑可以在空間中變形為另一條路徑，同時其端點保持固定，則兩條路徑定義相同的變換。這些變形，在技術上稱為同倫，對於路徑的組合定義結合運算是必要的，這是範疇所要求的。

基本群胚構造的一個關鍵優勢是它是“函子式的”，這意味著拓撲空間 X 和 Y 之間的連續函式 f: X → Y 產生基本群胚 π₁X 和 π₁Y 之間的相應變換 π₁f: π₁X → π₁Y。此賦值分別尊重組合和恆等式，這意味著 π₁(g ∘ f) = π₁g ∘ π₁f 和 π₁(1_X) = 1_π1X。這兩個統稱為“函子性”的屬性表明，基本群捕獲了關於拓撲空間的一些基本資訊。特別是，如果兩個空間不是同倫等價的，則它們的基本群胚必然是不等價的。

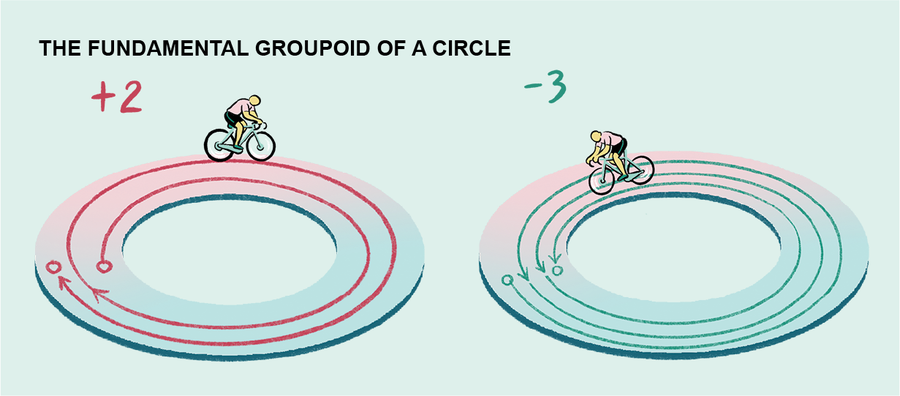
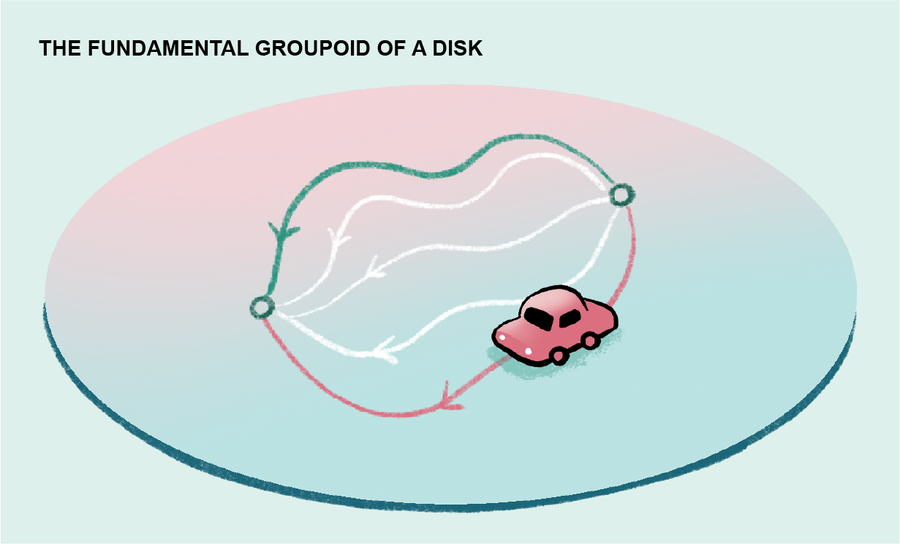
然而，基本群胚不是一個完整的不變式。它可以很容易地區分圓及其邊界的實心圓盤。在圓的基本群胚中，兩點之間路徑的不同擺動版本可以用整數標記，這些整數記錄軌跡繞圓纏繞的次數，以及分別指示順時針或逆時針方向的 + 或 − 符號。相比之下，在圓盤的基本群胚中，任何一對點之間最多隻有一個同倫路徑。由充氣沙灘球的外部形成的空間（拓撲術語中的球體）的基本群胚也具有此描述：任何兩個點之間最多隻有一個同倫路徑。

基本群胚的最大問題是點和路徑無法檢測空間的更高維度結構，因為點和區間本身分別是零維和一維的。一個解決方案是也考慮來自二維圓盤的連續函式，稱為同倫，以及“更高同倫”，由來自實心三維球的連續函式定義，對於 4、5、6 個或更多維度中的其他球也是如此。

自然要問，空間 X 中的點、路徑、同倫和更高同倫形成什麼樣的代數結構：這個結構 π _∞ X （“pi 無窮 X”），稱為 X 的基本 ∞-群胚，定義了 ∞-範疇的一個示例，∞-範疇是艾倫伯格和麥克萊恩首次引入的範疇的無限維類似物。像普通範疇一樣，∞-範疇具有物件和視覺化為一維箭頭的變換，但它也包含由二維箭頭、三維箭頭等描繪的“更高變換”。例如，在 π _∞X 中，物件和箭頭是點和路徑——不再考慮擺動——而更高維度的變換編碼更高同倫。像在普通範疇中一樣，任何固定維度中的箭頭都可以組合：如果您有兩個箭頭 f: X → Y 和 g: Y → Z, 則還必須有一個箭頭 g ∘ f: X → Z。 但是有一個問題：在試圖捕獲自然示例（例如空間的基本 ∞-群胚）時，組合律必須被削弱。對於任何可組合的箭頭對，都必須存在一個複合箭頭，但不再有唯一指定的複合箭頭。

這種唯一性的失敗使得在經典的基於集合的數學基礎上定義 ∞-範疇具有挑戰性，因為我們不能再將組合視為類似於泛代數中出現的運算。儘管 ∞-範疇在現代數學的許多領域（從量子場論到代數幾何再到代數拓撲學）中日益重要，但它們通常被認為“太難”，除了專家之外的所有人都難以理解，並且即使在研究生級別，也未定期在課程中出現。然而，許多其他人和我將 ∞-範疇視為革命性的新方向，它可以使數學家能夠夢想新的聯絡，否則這些聯絡將無法嚴格地陳述和證明。

未來的視野

然而，歷史經驗表明，今天最奇特的數學最終將被認為足夠容易，可以在未來教給數學本科生。作為 ∞-範疇論的研究人員，推測如何簡化這個學科是很有趣的。在這種情況下，有一個語言技巧——範疇“the”的超級版本——可以使 ∞-範疇像今天的普通範疇一樣容易讓 21 世紀後期的本科生思考。普通範疇中的關鍵公理是對於每對可組合的變換 f: X → Y 和 g: Y → Z, 存在唯一的複合變換 g ∘ f: X → Z, 從從 X 到 Z 的變換集合的所有元素中選擇。相比之下，在 ∞-範疇中，存在一個從 X 到 Z 的箭頭空間，在基本 ∞-群胚中，可以將其理解為一種“路徑空間”。普通範疇中複合唯一性的正確類似物是斷言在 ∞-範疇中，複合空間是“可收縮的”，這意味著它的每個點都可以透過反向大爆炸連續塌縮到單個原點。

請注意，可收縮性並不意味著存在唯一的複合：實際上，正如我們在基本 ∞-群胚中看到的那樣，可能存在大量複合路徑。但可收縮性保證任何兩條複合路徑是同倫的，連線兩條複合路徑的任何兩個同倫都透過更高的同倫連線，依此類推。

這種將唯一性作為一種可收縮性條件的想法是弗拉基米爾·沃埃沃德斯基等人提出的數學新基礎系統中的核心思想。世界各地的數學家正在合作開發新的基於計算機的“證明助手”，這些助手可以逐行檢查數學結果的形式證明。這些證明助手具有一種機制，可以模仿常見的數學實踐，即將關於一個事物的資訊轉移到透過顯式同構或同倫等價而被理解為相同的另一個事物。在這種情況下，該機制允許使用者沿著連線空間中一個點與任何其他點的路徑傳輸涉及該點的證明，從而給出拓撲學相同性概念的嚴格公式。

在 1974 年的一篇文章中，數學家邁克爾·阿蒂亞寫道，“理論的真正目標在很大程度上是系統地組織過去的經驗，以便下一代，我們的學生和他們的學生等等，能夠儘可能輕鬆地吸收基本方面，這是您可以持續累積地建立任何型別的科學活動而最終不會走到死衚衕的唯一方法。” 範疇論可以說是現代數學中的這種角色：如果數學是類比科學，是模式研究，那麼範疇論就是數學思想模式的研究——正如芝加哥藝術學院的歐金妮亞·鄭所說，“數學的數學”。

今天我們可以在本科課程中涵蓋如此多的內容的原因是，我們對各種數學概念的理解已透過抽象得到簡化，抽象可以被認為是退後一步考慮正在考慮的特定問題並採取更廣泛的數學觀點的過程。從這個層面上看不到很多精細的細節——例如，數值近似，或者實際上與數字有關的任何東西——但一個顯著的事實是，代數、集合論、拓撲學和代數幾何中的定理有時是出於相同的基本原因而成立的，當情況如此時，這些證明是用範疇論的語言表達的。

未來的視野是什麼？某些數學領域的共識是，21 世紀數學物件的自然棲息地是 ∞-範疇，就像 20 世紀數學物件的棲息地是普通範疇一樣。希望在 ∞-範疇中進行深入工作所需的每個維度中令人眼花繚亂的箭頭塔在某個時刻將退居集體數學潛意識的背景，每個可收縮的選擇空間都塌縮為一個唯一的點。人們只能想知道：如果在 20 世紀取得了如此大的進步，那麼數學在 21 世紀末會發展到什麼程度？