沃倫·巴菲特曾經挑戰比爾·蓋茨進行一場不尋常的骰子游戲。巴菲特在桌子上放了四個骰子,並解釋了規則。他們每人選擇一個骰子,擲幾次,誰擲出的數字更大次數更多,誰就獲勝。這些骰子的數字不像標準骰子那樣。通常的一到六被其他數字取代,這些數字因骰子而異。作為一種所謂的禮貌,巴菲特邀請蓋茨先選骰子。這引起了懷疑,促使蓋茨親自檢查骰子,然後堅持讓巴菲特先選。
通常,在遊戲中先選會帶來優勢,那麼為什麼這些大亨爭奪第二個選擇權呢?答案在於巴菲特骰子的一種特殊屬性。為了理解這一點,讓我們檢查一個與巴菲特使用的骰子具有相同屬性但更易於分析的類似骰子的例子。
來源:Amanda Montañez
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的有影響力的故事的未來。
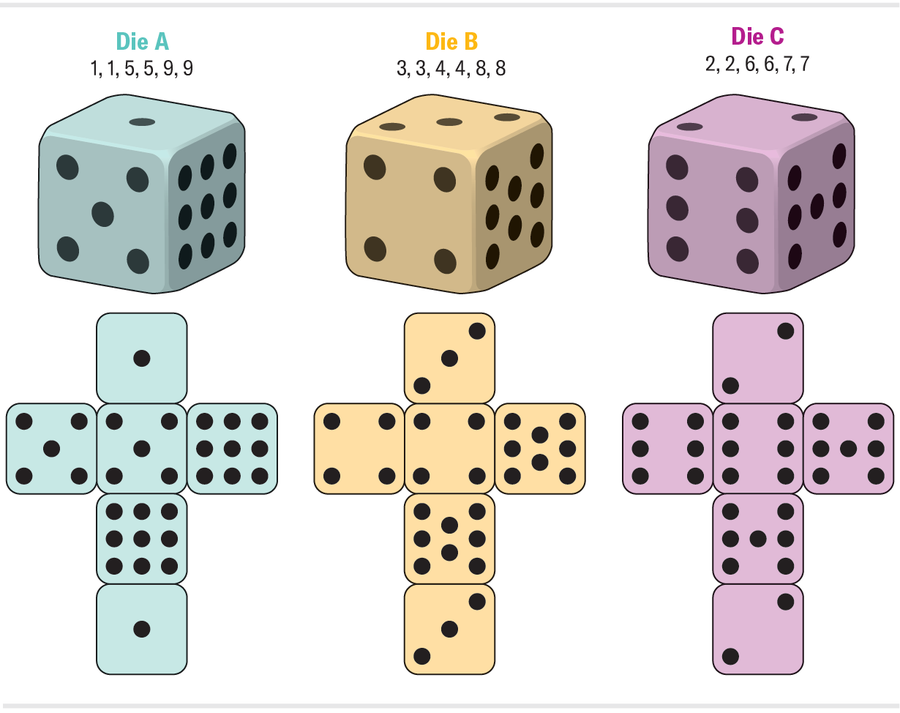
骰子 A 比骰子 B 擲出更高數字的頻率有多高?由於每個骰子上只有三個不同的數字,三分之一的時間,骰子 A 將擲出 9,無論 B 擲出什麼都會獲勝。三分之一的時間,A 將擲出 1,無論 B 擲出什麼都會輸。剩下的三分之一的時間,A 將擲出 5,這將在 B 的三分之二的擲骰中獲勝(擲出 3 或 4 的那些)。使用機率規則彙總這些觀察結果,我們得到 A 擊敗 B 的機率為 (⅓ x 1) + (⅓ x 0) + (⅓ x ⅔) = 5/9,約為 56%。類似的計算得出 B 擊敗 C 的機率也相同。也就是說,B 擊敗 C 的機率也約為 56%。因此,如果 A 通常擊敗 B,而 B 通常擊敗 C,那麼 A 肯定通常會擊敗 C,對嗎?錯了!C 實際上也擊敗 A 的機率約為 56%。
我們稱這些不守規矩的立方體為非傳遞骰子。生活中遇到的許多關係都表現出相反的傳遞性:如果艾麗西亞比布魯諾年長,而布魯諾比卡桑德拉年長,那麼艾麗西亞比卡桑德拉年長。這是一個有效的推論,因為“比……年長”的關係服從傳遞性。非傳遞骰子讓我們感到驚訝,因為“通常擲出更高數字”的關係不是傳遞的,儘管它看起來應該是傳遞的。請注意,為了平均擲出比骰子 B 更高的數字,骰子 A 不需要總是擲出更高的數字。至關重要的是,A 擊敗 B 的情況和 A 輸給 C 的情況之間存在重疊。面上的數字的這種交錯使得非傳遞性成為可能。
對於任何一組非傳遞骰子,在巴菲特的遊戲中先選的人都處於劣勢,因為第二個玩家總是可以選擇可能擊敗對手選擇的骰子。許多人最初透過石頭剪刀布遊戲接觸到非傳遞遊戲。其迴圈獲勝結構確保沒有一種選擇可以唯一地勝過任何其他選擇。巴菲特的骰子游戲類似於誘騙你的對手宣佈他們打算在石頭剪刀布遊戲中接下來出什麼——這是一個會讓他們輸掉遊戲的錯誤。
斯坦福統計學家布拉德利·埃夫隆在 50 多年前發明了非傳遞骰子。埃夫隆的四組骰子中的每個骰子擊敗另一個骰子的機率令人印象深刻,達到三分之二(約 67%)。馬丁·加德納在他的傳奇“數學遊戲”專欄中普及了埃夫隆的骰子《大眾科學》,但數學愛好者從那時起就設計了許多巧妙的變體。我們現在知道,任意數量的骰子(大於兩個)都可以表現出非傳遞迴圈,例如,存在一組 26 個骰子,其中骰子 A 通常擊敗骰子 B,骰子 B 通常擊敗 C,骰子 C 通常擊敗 D,依此類推,一直到骰子 Z,儘管骰子 Z 位於一系列佔優勢骰子的末端,但它卻透過迴圈返回並通常擊敗 A 來製造冷門。
非傳遞骰子不必包含六個面。事實上,具有任意數量面(大於兩個)的非傳遞三骰子存在。荷蘭謎題製造者奧斯卡·範·德文特甚至發明了一套七個六面骰子,允許三名玩家參與巴菲特的遊戲。換句話說,如果巴菲特和蓋茨邀請多莉·帕頓與他們一起玩骰子,那麼蓋茨和帕頓可以各自從七個骰子中選擇,而巴菲特仍然總能在剩下的五個骰子中找到一個通常擊敗他們兩人選擇的骰子。
就在你認為你已經理解了非傳遞骰子的奇特行為時,下面這個絕妙的構造會讓你再次震驚得說不出話來。
來源:Amanda Montañez
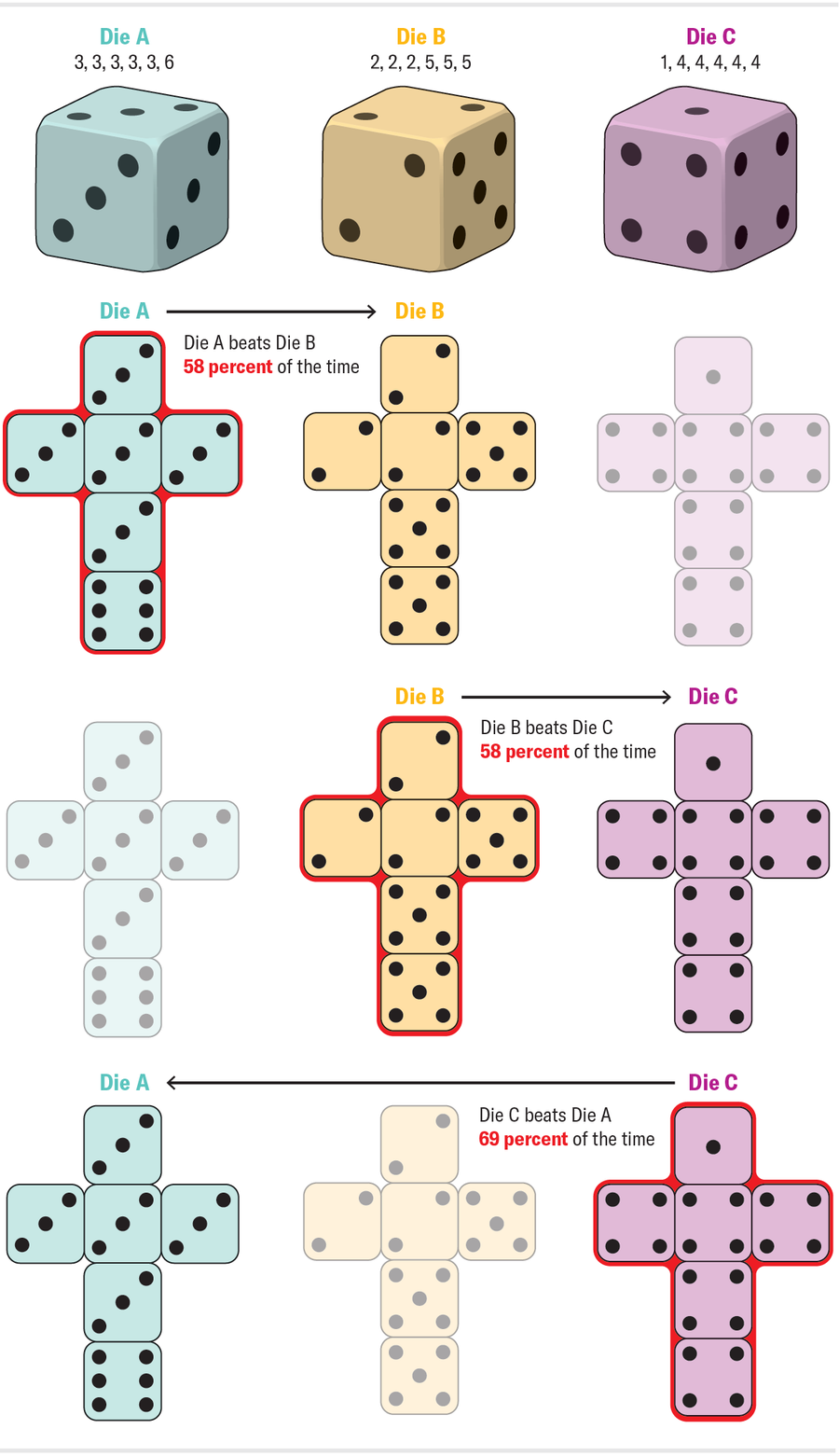
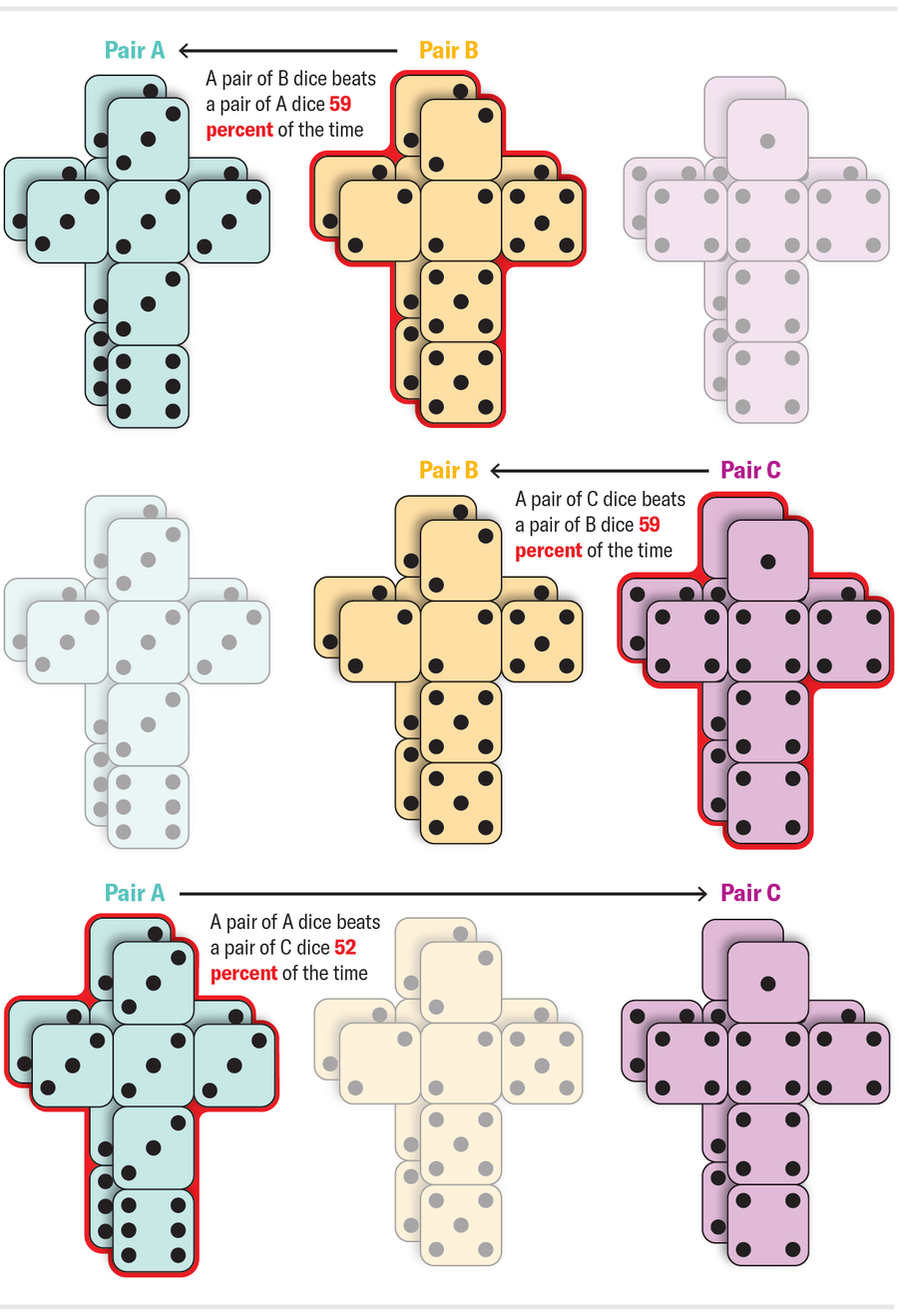
可以計算出 A 擊敗 B 的機率為 7/12(約 58%);B 擊敗 C 的機率為 7/12;C 擊敗 A 的機率為 25/36(約 69%)。到目前為止,沒有什麼我們以前沒見過的。這些骰子彼此擊敗的機率並不完全相同,但它們仍然是非傳遞的。骰子通常成對出現。當您想象擲骰子時,您可能會想到手中拿著兩個相同的骰子,並將每個骰子上出現的數字相加。如果我們從上圖擲出成對的骰子會發生什麼?兩個骰子 A 擲出的總和擊敗兩個骰子 B 擲出的總和的機率是多少?由於骰子是相同的,它是否與以前相同,或者複製骰子是否會放大 A 對 B 的優勢?在一個令人震驚的轉折中,效果逆轉了。一對骰子 A 通常輸給一對骰子 B!更重要的是,整個迴圈都逆轉了:一對骰子 B 通常輸給一對骰子 C,而一對骰子 C 通常輸給一對骰子 A。購買一套這樣的骰子是可靠的被禁止參加家庭遊戲之夜的方法。
來源:Amanda Montañez
為了感受複製骰子如何逆轉它們的相對強度,想象一下兩個兩面骰子 X 和 Y 的簡單情況。X 的兩個面都有數字 1,而 Y 的面是 0 和 3。這些骰子的強度相等。Y 有一半的時間獲勝(當它擲出 3 時),一半的時間輸掉(當它擲出 0 時)。但是,當我們複製骰子時,骰子 Y 對變得比骰子 X 對更強。骰子 X 對總是擲出總共 2。骰子 Y 對只有在它們都擲出 0 時才會輸,而這種情況只發生在四分之一的時間。類似的現象解釋了上圖中的逆轉。
非傳遞骰子應該存在根本不明顯。但這是否是因為它們很少見?如果您對一組三個骰子所知甚少,只知道 A 通常擊敗 B,而 B 通常擊敗 C,那麼 A 通常擊敗 C 還是反之亦然的可能性更大?聰明的人已經手工精心構造了上面討論的所有骰子,但是他們是否可以只是隨機選擇骰子編號,並有很大的機會找到非傳遞集合?
英國數學家蒂莫西·高爾斯著手回答這個問題。高爾斯領導著Polymath 專案,這是一種創新且相對較新的數學研究範例。Polymath 專案沒有像典型的數學研究模型那樣,由一兩所大學的少數數學家啃硬骨頭地解決問題,而是採用了眾包方法。任何數量的貢獻者都可以透過線上論壇討論來合作證明。高爾斯認為非傳遞骰子問題適合集體努力,並於 2017 年在他的部落格上提出了這個問題。用 WordPress 評論區取代黑板,數十位頭腦風暴了這個問題並破解了它。
如果您隨機為三個不同的骰子分配數字,然後想知道它們是否表現出非傳遞性的機率,這可能取決於您對“隨機分配數字”給骰子的確切含義。Polymath 團隊使用兩個自然標準對此進行了建模。正如典型的六面骰子只包含 1 到 6 之間的數字一樣,隨機的n面骰子也只包含 1 到n之間的數字(儘管有些可能會重複,有些可能根本不會出現)。此外,典型六面骰子上的數字加起來為 1 + 2 + 3 + 4 + 5 + 6。為了保持骰子的平衡(例如,沒有骰子應該包含全部為 1 或全部為巨大數字),Polymath 團隊對n面骰子提出了以下要求:它們的面之和應等於從 1 到n的數字之和。
你想猜測傳遞骰子還是非傳遞骰子更常見嗎?Polymath 專案參與者證明,三個隨機的 n 面骰子將大約一半的時間是非傳遞的。換句話說,知道 A 通常擊敗 B,而 B 通常擊敗 C,幾乎不能為您提供關於 A 通常會擊敗 C 還是反之亦然的資訊。我本以為傳遞骰子比非傳遞骰子更常見。我可以想象一些多疑的讀者,厭倦了他們的期望被顛覆,預測非傳遞骰子比傳遞骰子更常見。但是這些狡猾的骰子堅持要逃避預測。對於三個骰子,傳遞骰子和非傳遞骰子同樣常見。
