物理學定律規定,凡是不被禁止的都是強制性的。因此,錯誤是不可避免的。它們無處不在:在語言、烹飪、交流、影像處理,當然還有計算中。減輕和糾正錯誤使社會得以運轉。您可以刮擦 DVD,但仍然可以播放它。二維碼可能會模糊或撕裂,但仍然可讀。來自太空探測器的影像可以傳播數億英里,但仍然看起來清晰。糾錯是資訊科技中最基本的概念之一。錯誤可能是不可避免的,但它們也是可以修復的。
這條不可避免性定律同樣適用於量子計算機。這些新興機器利用基本的物理學規則來解決經典計算機認為棘手的問題。對科學和商業的影響可能是深遠的。但是,強大的力量伴隨著巨大的脆弱性。量子計算機遭受經典計算機所未知型別的錯誤,而我們標準的糾錯技術無法修復這些錯誤。
我是一名在 IBM 從事量子計算的物理學家,但我的職業生涯並非從那裡開始。我最初是一名凝聚態理論家,研究材料的量子力學行為,例如超導性;當時我並沒有意識到這最終會如何引導我走向量子計算。那是後來我休假去美國國務院從事科學政策工作時才發生的,這之後又引導我去了國防高階研究計劃局 (DARPA) 和情報高階研究計劃活動 (IARPA)。在那裡,我試圖利用自然的基本原理來開發新技術。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
當時的量子計算機還處於最早階段。儘管阿貢國家實驗室的保羅·貝尼奧夫在 1980 年就提出了它們,但物理學家花了將近二十年的時間才建造出第一臺。又過了十年,在 2007 年,他們發明了構成 IBM、谷歌和其他公司的量子計算機基礎的基本資料單元,稱為 超導 Transmon 量子位元。我對超導性的經驗突然變得搶手。我幫助在 IARPA 運行了幾個量子計算研究專案,後來加入了 IBM。
在那裡,我致力於改進多個連結量子位元之間的操作,並探索如何糾正錯誤。透過量子現象(稱為糾纏)組合量子位元,我們可以集體儲存大量資訊,遠遠超過相同數量的普通計算機位元所能儲存的資訊。由於量子位元狀態以波的形式存在,它們可以像光波一樣干涉,從而產生比僅翻轉位元更豐富的計算前景。這些能力使量子計算機能夠非常高效地執行某些功能,並有可能加速廣泛的應用:模擬自然、研究和工程新材料、揭示資料中的隱藏特徵以改進機器學習,或為工業化學過程尋找更節能的催化劑。
問題在於,許多解決有用問題的提案要求量子計算機在成百上千個量子位元上執行數十億次邏輯運算或“門”。這需要它們在每十億個門中最多犯一個錯誤。然而,當今最好的機器每 1,000 個門就會犯一個錯誤。面對理論與實踐之間的巨大差距,早期的物理學家擔心量子計算將仍然是科學上的好奇之物。
糾正錯誤
1995 年,貝爾實驗室的彼得·肖爾和牛津大學的安德魯·斯蒂恩獨立開發了量子糾錯技術,這改變了遊戲規則。他們展示了物理學家如何將單個量子位元的資訊分散到多個物理量子位元上,從而用不可靠的元件構建可靠的量子計算機。只要物理量子位元的質量足夠高,使其錯誤率低於某個閾值,我們就可以比錯誤積累的速度更快地消除錯誤。
為了理解肖爾和斯蒂恩的工作如此突破性的原因,請考慮普通糾錯通常是如何工作的。一個簡單的糾錯碼會備份資訊——例如,用 000 表示 0,用 111 表示 1。這樣,如果您的計算機讀出 010,它就知道原始值可能為 0。當錯誤率足夠低,以至於最多隻有一個位元副本被損壞時,這種程式碼就會成功。工程師會盡可能使硬體可靠,然後新增一層冗餘來清除任何剩餘的錯誤。

圖片來源:Jen Christiansen
然而,尚不清楚如何將經典糾錯方法應用於量子計算機。量子資訊無法複製;為了糾正錯誤,我們需要透過測量來收集有關錯誤的資訊。問題是,如果您檢查量子位元,您可能會坍縮它們的狀態——也就是說,您可能會破壞其中編碼的量子資訊。此外,除了位元翻轉錯誤外,在量子計算機中,您還會有描述量子位元狀態的波的相位錯誤。
為了繞過所有這些問題,量子糾錯策略使用輔助量子位元。一系列門將輔助量子位元與原始量子位元糾纏在一起,這有效地將噪聲從系統轉移到輔助量子位元。然後您測量輔助量子位元,這為您提供了足夠的資訊來識別錯誤,而無需接觸您關心的系統,從而讓您修復它們。

圖片來源:Jen Christiansen
與經典糾錯一樣,成功取決於噪聲的物理特性。對於量子計算機,當裝置與環境糾纏時,就會出現錯誤。為了保持計算機正常工作,物理錯誤率必須足夠小。此錯誤率存在一個臨界值。低於此閾值,您可以糾正錯誤,使計算失敗的機率任意低。高於此閾值,硬體引入錯誤的速度快於我們糾正錯誤的速度。這種行為的轉變本質上是有序狀態和無序狀態之間的相變。作為一名理論凝聚態物理學家,我職業生涯的大部分時間都在研究量子相變,這讓我著迷。
我們正在繼續研究改進糾錯碼的方法,以便它們可以處理更高的錯誤率、更廣泛的錯誤型別以及硬體的約束。最流行的糾錯碼稱為拓撲量子碼。它們的起源可以追溯到 1982 年,當時麻省理工學院的弗蘭克·維爾切克提出宇宙可能包含一種全新的粒子類別。與已知的型別(具有整數或半奇數整數值的角動量)不同,新型別可能具有介於兩者之間的分數值。他稱它們為“任意子”,並告誡說“這些現象的實際應用似乎遙不可及。”
圖片來源:Jen Christiansen
但很快物理學家發現任意子並非那麼深奧;事實上,它們與現實世界的現象有關。為了完成它們從理論到技術實際需求的遷移,加州理工學院的阿列克謝·基塔耶夫意識到任意子是量子計算的一種有用的公式。他進一步提出使用某些多粒子系統作為量子糾錯碼。
在這些系統中,粒子以晶格結構連線,其中它們的最低能量狀態高度糾纏。錯誤對應於系統處於更高的能量狀態,稱為激發。這些激發是任意子。該系統標誌著拓撲碼的誕生——以及凝聚態物理學和量子糾錯之間的又一個聯絡。由於噪聲預計會區域性作用於晶格,而拓撲碼具有區域性激發,因此它們很快成為保護量子資訊的首選方案。
圖片來源:Jen Christiansen
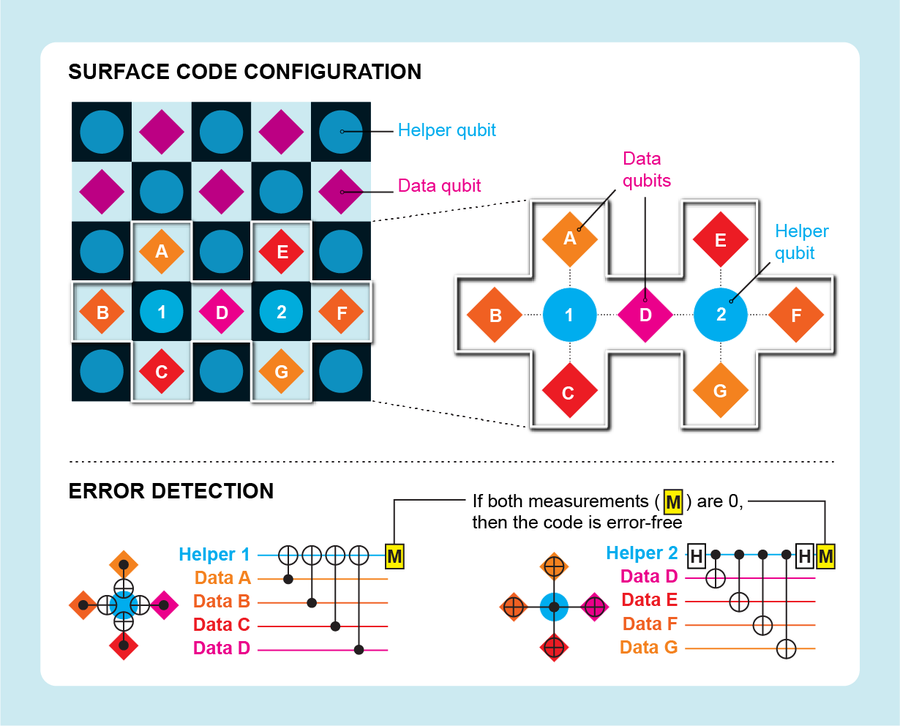
拓撲碼的兩個例子稱為表面碼和顏色碼。表面碼由基塔耶夫和我的 IBM 同事謝爾蓋·布拉維建立。它以二維正方形網格上的資料和輔助量子位元交替為特徵,就像棋盤上的黑白方格一樣。
從棋盤到卡坦島拓荒者
表面碼背後的理論引人入勝,但當我們在 IBM 開始探索它們時,我們遇到了挑戰。理解這些需要更多關於 Transmon 量子位元如何工作的知識。
Transmon 量子位元依賴於超導線電路中流動的振盪電流。量子位元 0 和 1 值對應於電荷的不同疊加。為了對量子位元執行操作,我們以特定頻率施加微波能量脈衝。我們在選擇頻率方面有一定的靈活性,我們在製造量子位元時設定頻率,為不同的量子位元選擇不同的頻率,以便能夠單獨定址它們。問題在於頻率可能偏離預期值,或者脈衝可能在頻率上重疊,因此 предназначен для 一個量子位元的脈衝可能會改變相鄰量子位元的值。表面碼的密集網格,其中每個量子位元與四個其他量子位元連線,導致了太多的頻率衝突。
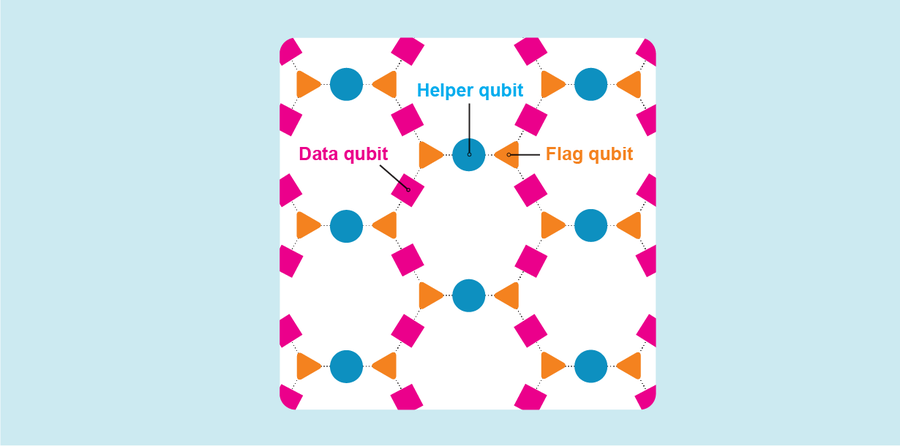
我們的團隊決定透過減少每個量子位元連線的鄰居數量來解決這個問題。由此產生的晶格由六邊形組成——我們稱之為“重六邊形”佈局——看起來更像是卡坦島拓荒者遊戲板,而不是棋盤。好訊息是,重六邊形佈局減少了頻率衝突的頻率。但是,為了使這種佈局有價值,IBM 理論團隊必須開發一種新的糾錯碼。
新程式碼稱為重六邊形程式碼,結合了表面程式碼和另一種基於晶格的程式碼(稱為 Bacon-Shor 程式碼)的特徵。我們程式碼中較低的量子位元連線性意味著一些量子位元(稱為標誌量子位元)必須充當中間人來識別發生了哪些錯誤,從而導致電路稍微複雜一些,因此成功的錯誤閾值略低。但是我們發現這種權衡是值得的。
還有一個問題尚未解決。生活在二維平面上並且僅包含最近鄰連線的程式碼具有很大的開銷。糾正更多錯誤意味著構建更大的程式碼,這需要使用更多的物理量子位元來建立一個邏輯量子位元。該設定需要更多的物理硬體來表示相同數量的資料——而更多的硬體使得構建足夠好的量子位元以擊敗錯誤閾值變得更加困難。
量子工程師有兩個選擇。我們可以接受大的開銷——額外的量子位元和門——作為更簡單架構的成本,並努力理解和最佳化導致成本的不同因素。或者,我們可以繼續尋求更好的程式碼。例如,為了將更多邏輯量子位元編碼到更少的物理量子位元中,也許我們應該允許量子位元與比最近鄰更遠的量子位元相互作用,或者超越二維網格到三維或更高維晶格。我們的理論團隊正在追求這兩種選擇。
通用性的重要性
有用的量子計算機必須能夠執行任何可能的計算操作。忽略這一要求是許多關於量子計算的常見誤解和誤導性資訊的根源。簡而言之,並非所有人們稱之為量子“計算機”的裝置實際上都是計算機——許多裝置更像是隻能執行某些任務的計算機器。
忽視通用計算的需要也是關於邏輯量子位元和量子糾錯的誤解和誤導性資訊的根源。保護記憶體中的資訊免受錯誤影響是一個開始,但這還不夠。我們需要一組通用的量子門,這組量子門必須足夠豐富,才能執行量子物理學允許的任何門。然後我們需要使這些門對錯誤具有魯棒性。這就是事情變得困難的地方。
有些門很容易防止錯誤——它們屬於稱為橫向門的類別。為了理解這些門,請考慮兩個描述級別:邏輯量子位元(受錯誤保護的資訊單元)和物理量子位元(協同工作的硬體級裝置,用於編碼和保護邏輯量子位元)。為了執行受錯誤保護的單量子位元橫向門,您需要對編碼邏輯量子位元的所有物理量子位元執行該門。為了在多個邏輯量子位元之間操作受錯誤保護的橫向門,您需要在邏輯量子位元中相應的物理量子位元之間操作該門。您可以將邏輯量子位元視為兩個物理量子位元塊,分別稱為塊 A 和塊 B。為了實現邏輯(即受錯誤保護的)橫向門,您需要在塊 A 的量子位元 1 和塊 B 的量子位元 1 之間、塊 A 的量子位元 2 和塊 B 的量子位元 2 之間執行該門,依此類推,適用於塊中的所有量子位元。由於只有相應的量子位元在相互作用,因此橫向門使每個塊的錯誤數量保持不變,因此處於受控狀態。
如果整個通用量子門集都是橫向的,那麼生活就會變得輕鬆。但是,一個基本定理指出,沒有量子糾錯碼可以僅使用橫向門執行通用計算。我們不可能在生活中擁有一切——或者在量子糾錯中也不可能。
這告訴我們一些關於量子計算機的重要資訊。如果您聽到任何人說量子計算的特別之處在於您擁有疊加和糾纏,請當心!並非所有的疊加和糾纏態都是特殊的。有些是由一組我們稱為 Clifford 群的橫向門實現的。經典計算機可以使用僅 Clifford 門有效地模擬量子計算。您需要的是非 Clifford 門,它們往往不是橫向的,並且很難進行經典模擬。
我們擁有的保護非 Clifford 門免受噪聲影響的最佳技巧稱為 魔術態蒸餾,由基塔耶夫和布拉維開發。如果您可以使用稱為魔術態的特殊資源,則可以使用僅 Clifford 門來實現非 Clifford 門。然而,這些魔術態必須非常純淨——換句話說,錯誤非常少。基塔耶夫和布拉維意識到,在某些情況下,您可以從收集的嘈雜魔術態開始,並透過僅使用完美的 Clifford 門(這裡您假設 Clifford 門已經過糾錯)和測量來檢測和糾正錯誤,從而將它們蒸餾出來,最終得到更少但更純淨的魔術態。多次重複蒸餾過程,您可以從許多嘈雜的魔術態中獲得純淨的魔術態。
一旦您擁有了純淨的魔術態,您就可以使用稱為隱形傳態的過程使其與資料量子位元相互作用,該過程將資料量子位元的狀態轉移到非 Clifford 門本應產生的新狀態。魔術態在此過程中被消耗掉。
儘管這種方法很聰明,但它也非常昂貴。對於標準表面碼,魔術態蒸餾消耗了 99% 的整體計算量。顯然,我們需要改進或規避對魔術態蒸餾的需求的方法。與此同時,我們可以透過使用錯誤緩解來推進我們使用嘈雜量子計算機可以做的事情。錯誤緩解不是試圖設計量子電路來即時修復計算中的錯誤(需要額外的量子位元),而是使用經典計算機從嘈雜實驗的結果中學習噪聲的貢獻並消除它。您不需要額外的量子位元,但您需要付出執行更多量子電路和引入更多經典處理的代價。
例如,如果您可以表徵量子處理器中的噪聲,或者從可以在經典計算機中有效模擬的嘈雜電路的訓練集中學習噪聲,則可以使用該知識來近似理想量子電路的輸出。將該電路視為嘈雜電路的總和,每個電路都有一個您從噪聲知識中計算出的權重。或者多次執行電路,每次更改噪聲值。然後,您可以獲取結果,連線點,並外推到您期望系統無錯誤時的結果。
這些技術存在侷限性。它們並非適用於所有演算法,即使適用,它們也只能讓您走這麼遠。但是,將錯誤緩解與糾錯相結合會產生強大的聯合。我們的理論團隊最近表明,透過對 Clifford 門使用糾錯,對非 Clifford 門使用錯誤緩解,這種方法可以讓我們模擬通用量子電路,而無需魔術態蒸餾。這種結果也可能使我們能夠使用較小的量子計算機獲得優於經典計算機的優勢。該團隊估計,錯誤緩解和糾錯的特定組合使您可以模擬涉及的非 Clifford 門比經典計算機可以處理的門多 40 倍。
為了向前發展並設計更有效的錯誤處理方法,硬體和理論之間必須存在緊密的反饋迴圈。理論家需要使量子電路和糾錯碼適應機器的工程約束。工程師應該圍繞糾錯碼的需求設計系統。量子計算機的成功取決於駕馭這些理論和工程權衡。
我為在將量子計算從基於實驗室的單量子位元和雙量子位元裝置演示領域發展到任何人都可以透過雲訪問具有數十個量子位元的量子系統的領域中發揮作用而感到自豪。但我們還有很多工作要做。要收穫量子計算的好處,需要低於錯誤閾值執行的硬體、可以儘可能少地使用額外量子位元和門來修復剩餘故障的糾錯碼,以及更好地結合糾錯和緩解的方法。我們必須繼續前進,因為我們尚未完成編寫計算的歷史。

