18世紀,普魯士城市柯尼斯堡的居民們苦苦思索著一個難題:他們如何才能找到一條穿過城市的步行路線,恰好一次走過其著名的七座橋樑?
這些橋樑橫跨一條河流,河流中包含兩個大島。無論他們如何規劃路線,都無法避免重複走過一座橋。
這個問題難住了當地的思想家,他們最終寫信給著名數學家萊昂哈德·尤拉(發音為“奧伊勒”),懇求他平息他們的好奇心。尤拉不屑一顧地回應道,聲稱這個問題與“數學幾乎沒有關係”。在某種程度上,他是對的,因為相關的數學尚未被髮明出來。儘管他最初表示拒絕,但尤拉最終還是解決了柯尼斯堡七橋問題,他沒有意識到,在這個過程中,他開創了兩個新的數學分支。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。 透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和思想的具有影響力的故事的未來。
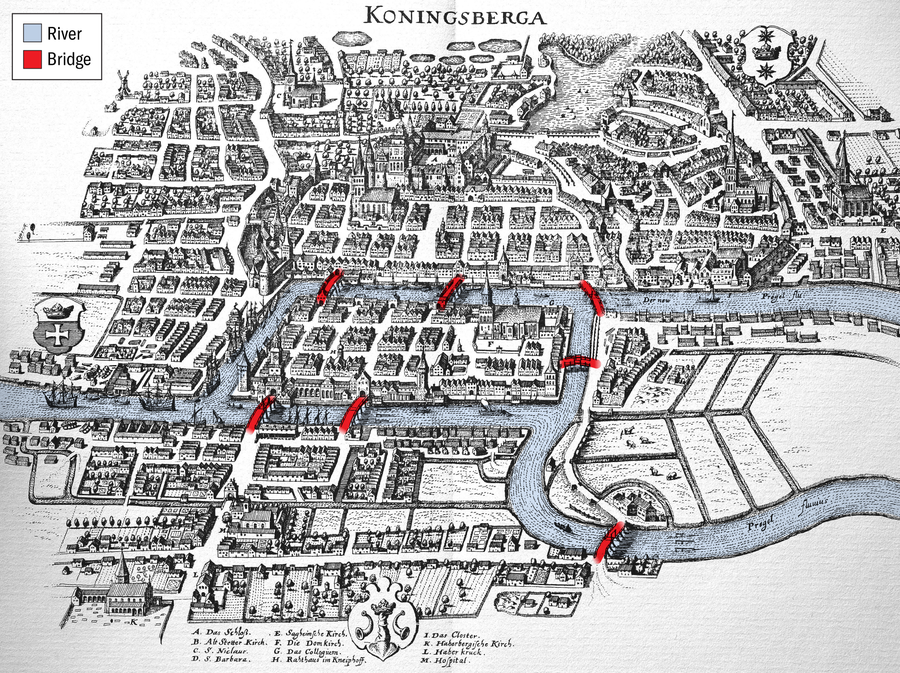
中世紀的普魯士城市柯尼斯堡,現在是俄羅斯的加里寧格勒。 這張18世紀的城市地圖是經過數字增強的複製品,經過修改以突出河流和橋樑。
圖片來源:Alamy Stock Photo(地圖);阿曼達·蒙塔內斯(突出顯示)
假設您是柯尼斯堡的居民。看著上面的地圖,您能設計出一條遍歷每座橋樑一次的路徑嗎?您必須像數學家一樣思考。解決任何數學問題的第一個障礙是剝離無關資訊,直到只剩下必要的要素,這個過程稱為抽象。地圖的許多特徵並不影響手頭的問題。橋樑的長度、陸地的大小,甚至陸地和橋樑的地理方位都可以忽略不計。重要的是哪些陸地塊與哪些其他陸地塊相連,以及連線多少次。現在我們可以建立一個更簡單的圖表,僅由圓圈和線條組成,分別代表陸地和橋樑。
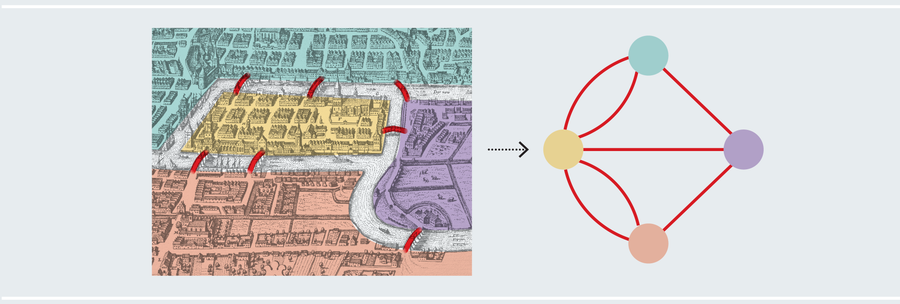
圖片來源:Alamy Stock Photo(地圖);阿曼達·蒙塔內斯(突出顯示和圖表)
現代數學術語稱之為“圖”,不要與其他不相關的數學圖(如 x-y 平面中的繪圖或統計視覺化(如條形圖))混淆。或許“網路”會是一個更好的術語,以避免任何混淆。我們稱圓圈為“頂點”,線條為“邊”。如今,圖論是數學和計算機科學的一個主要領域,應用範圍廣泛。圖不必代表陸地和橋樑。它們可以代表社交網路、蛋白質相互作用、州界、神經網路、全球資訊網或任何其他涉及成對關係的資料。
抽象使數學家能夠將一個關於舊城市特定橋樑排列的高度具體問題轉化為關於所有圖的一般問題。給定一個具有任意數量頂點和邊的圖,是否存在一條恰好遍歷每條邊的路徑?事實證明,一個非常簡單的測試可以回答任何圖的這個問題:對於每個頂點(我們當前難題中的陸地),計算從它發出的邊的數量(橋樑)。如果所有這些計數都是偶數,或者如果除了兩個之外的所有計數都是偶數,則路徑存在;否則,路徑是不可能的。
讓我們探討一下其中的道理。想象一條穿過圖的路徑,該路徑恰好穿過每條邊一次。考慮該路徑中間的頂點(不是起點或終點頂點)。如果該頂點有很多邊,那麼您的路徑將多次訪問它,但是每次您進入頂點時,也必須透過不同的邊退出它。因此,路徑中間的頂點每次被訪問時,兩條邊都會被訪問。這隻有在路徑中間的每個頂點都有偶數條邊的情況下才有效。路徑的起點和終點是唯一的例外,因為起點不必進入,而終點不必退出。因此,如果我們恰好有兩個具有奇數條邊的頂點,那麼如果您從這些頂點開始和結束,我們的路徑是可能的。如果每個頂點都有偶數條邊,那麼將存在一條路徑,該路徑從同一頂點開始和結束,形成一個環路。
這個論證被認為是圖論中的第一個成果,而穿過圖並訪問每條邊一次的路徑現在被稱為尤拉路徑。 從技術上講,尤拉的論證僅描述了使尤拉路徑不可能存在的條件,而在這些條件下尤拉路徑始終存在的證明是後來才出現的。將我們所學到的知識應用於柯尼斯堡的橋樑,我們看到所有四個頂點都有奇數條邊從它們發出,這意味著,唉,普魯士的漫步者徒勞地尋找了。
這是一個奇特的旁註。找到一條穿過圖並恰好訪問每個頂點(我們示例中的陸地而不是橋樑)一次的路徑,聽起來像是一個密切相關的問題,但實際上是一個完全不同的難題。雖然一個簡單的測試可以確定一個圖是否包含尤拉路徑,但我們不知道任何通用的高效程式來解決這個以頂點為中心的變體。這個變體被稱為哈密頓路徑問題,它屬於一類被廣泛認為計算上難以處理的問題。
儘管尤拉最初對橋樑問題嗤之以鼻,但他最終還是被他無法用他常用的工具包解決這個問題所吸引。他給一位朋友寫信說:“這個問題是如此平庸,但在我看來值得關注,因為幾何學、代數學,甚至計數的藝術都不足以解決它。” 當時,幾何學關注的是距離、角度和麵積等定量概念。但是,雖然橋樑問題在本質上似乎是幾何的,但它並沒有要求任何型別的測量。這個問題需要一種新的抽象,這種抽象忽略了傳統的幾何量,同時尊重了問題核心的成對連線。
將柯尼斯堡地圖簡化為一個簡單的圖的想法在事後看來似乎很明顯,但許多最好的抽象都是如此。數學史講述了抽象的力量。如果古代數學思想家有關於橙子、珍珠甚至地球的定量問題,他們可以開發定製的語言和技術來應對每個新的挑戰。但是,一旦人們認識到這些看似不同的物件都例項化了相同的高階實體:球體,這項工作就變得容易和清晰得多。給抽象一個名稱和一個定義,就允許從未見過面的人們在彼此的工作基礎上進行構建,而無需重新發明輪子。
尤拉的論文不僅開創了圖論領域,而且還為另一個主要的數學分支奠定了基礎,即拓撲學。拓撲學指的是研究幾何性質,即使我們像對待由高彈性橡膠製成的物體一樣拉伸、壓縮或變形物體,這些幾何性質仍然存在。因此,雖然一個層次的抽象將我們從現實世界的物體(如橙子、山脈和骰子)帶到它們的形狀(球體、金字塔和立方體),但拓撲學引入了第二個抽象層次,在這個層次中,我們將球體、金字塔和立方體視為某些甚至更高階實體的例項化。拓撲學家認為這些固體是等價的,因為它們都可以在橡膠世界中被塑造成彼此,而不像甜甜圈,無論你如何拉伸它,甜甜圈都會保持一個孔。
透過抽象掉柯尼斯堡地圖中的定量細節,尤拉為一種新的幾何思維方式打開了大門,這種思維方式擺脫了千年來一直主導該學科的距離和角度的定量細節。圖論和拓撲學今天繼續產生新的數學見解,我們應該感謝逝去的漫步文明。