在2018年4月17日上午11:03,金屬疲勞導致西南航空1380次航班(從紐約飛往達拉斯,飛行高度32,000英尺)左側引擎內部的一個風扇葉片斷裂。斷裂炸開了引擎外殼,金屬碎片撞擊機身,擊碎了14排的一個窗戶。隨之而來的急速客艙減壓導致一名乘客被吸出受損的窗戶半個身子,並受到致命傷。飛行員成功地在費城安全降落飛機,避免了更大的悲劇。
多年來,由金屬疲勞引起的飛機事故數量一直在穩步增加,在最近統計的2010年代達到高峰,為30起。其中幾起事件嚴重到需要緊急迫降。雖然2024年1月波音737 Max 9飛機門塞在16,000英尺高空脫落事件可能是由於螺栓缺失,但Max系列飛機在2019年曾發生過一起與疲勞相關的安全問題,當時易發生裂縫的機翼前緣縫翼不得不更換。
飛機被形容為“兩百萬個零件組成的密集編隊飛行”,很多地方都可能出錯。連續的飛行使這些零件經受強烈的應力和鬆弛迴圈,在此期間,製造過程中不可避免的小缺陷可能導致微小的裂縫。一旦裂縫長到足夠長,就像西南航空1380次航班的風扇葉片底部發生的那樣,相鄰的部件可能會斷裂脫落。因此,飛機設計師需要預測部件必須承受的最大應力。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
裂縫可能出現在像大壩、橋樑和建築物這樣巨大的結構中,也可能出現在像我們自己身體裡的骨骼和牙齒這樣生物學上密切相關的結構中。例如,美國國家標準與技術研究院的工程師正在對2021年佛羅里達州海濱公寓的倒塌事件進行建模,以瞭解支撐結構中的裂縫可能在災難中起到的作用。最近對在北大西洋內爆的泰坦號潛水器的分析已經確定了可能發生斷裂的區域。在金屬、混凝土和牙釉質中,裂縫形成於承受最大應力的區域——當裂縫超過臨界長度時,它們可能是最危險的,而臨界長度取決於材料。
工程師可以使用類似的工具來研究各種各樣的裂縫並防止故障。作為防止故障的重要防禦措施,機器或結構應進行物理測試,但這種測試可能很昂貴,並且可能並非總是可行。一旦部件投入使用,就應定期檢查,這也非常昂貴。
除了這些實踐策略之外,還有防止故障的第三個關鍵方面:計算機模擬。在開發過程中,模擬有助於工程師建立和測試在許多不同條件下應保持可行的設計,並且可以針對強度和重量等因素進行最佳化。例如,飛機需要儘可能輕便耐用。如果操作得當,模擬可以幫助防止事故發生。
隨著美國啟動大規模的基礎設施改造計劃,提高計算機模擬的可靠性可以幫助確保安全。
這些模擬的可靠性對於安全至關重要——但它們沒有像製造缺陷、維護錯誤或檢查頻率那樣受到同樣的審查或監管。分析1991年挪威石油平臺倒塌事件的工程師發現,由於模擬錯誤,其中一個內部支撐牆的預計應力僅為實際應力的一半左右。因此,它的設計加固比需要的要輕得多,結果就失效了。
隨著美國啟動大規模的基礎設施改造計劃,確保安全性和耐久性將至關重要。可靠的計算機模擬可以幫助實現這兩者,同時減少對昂貴的物理測試的需求。然而,令人擔憂的是,工程師使用的模擬通常不如它們需要的那樣可靠。數學正在展示如何改進它們,從而使汽車、飛機、建築物、橋樑以及其他物體和結構更安全且更便宜。
考慮到21世紀機器的複雜性,17世紀70年代釋出的字謎竟然是其力學的基礎,這真是令人好奇。被稱為胡克定律的ut tensio, sic vis(“伸長量與力成正比”)指出,彈性物體(如金屬彈簧)的形變與施加在其上的力成正比。只有當物體保持彈性時,該定律才仍然有效——也就是說,如果當力移除時,物體恢復到其原始形狀。當力變得過大時,胡克定律不再適用。
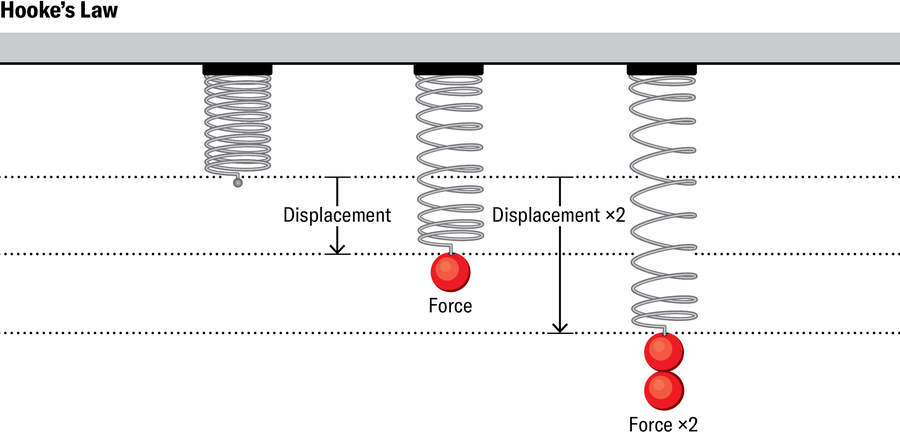
珍·克里斯蒂安森
在更高維度中,情況變得更加複雜。想象一下輕輕按下粘在桌子上的橡膠立方體。在這種情況下,立方體的高度與其原始高度相比的減少量,即“應變”,與您施加在立方體頂面單位面積上的力,即“應力”成正比。人們還可以以不同的角度對不同的面施加不同的力——用工程師的話說,讓立方體承受不同的“載荷”。然後,應力和應變都將具有多個分量,並且通常會逐點變化。胡克定律的廣義形式仍然成立,前提是載荷不要太大。它表示應力和應變仍然成正比,儘管方式更復雜。例如,將所有應力加倍仍然會使所有應變加倍。
人們使用胡克定律來分析各種各樣的材料——金屬、混凝土、橡膠,甚至骨骼。(該定律適用的力範圍取決於材料的彈性。)但該定律僅提供了確定物體將如何響應實際載荷所需的多條資訊之一。工程師還必須考慮作用在物體上的所有力的平衡,包括內部和外部力,並指定應變如何與不同方向的變形相關聯。最終得到的方程稱為偏微分方程 (PDE),它涉及諸如應力和應變等量在不同方向上的變化率。它們過於複雜,無法手工求解,甚至無法精確求解,特別是對於在風扇葉片和橋樑支架等中遇到的複雜幾何形狀。
即便如此,最值得注意的是,從1967年弗拉基米爾·孔德拉季耶夫開始,數學家們已經分析了這些 PDE 在常見幾何形狀(如多邊形和多面體)中的應用,以獲得有價值的見解。例如,應力通常在任何角和邊緣附近最高。這就是為什麼如果您先切開一個小口,然後從切口處開始拉開箔紙,就更容易撕開一張箔紙。
問題在於,許多對其完整性對於安全至關重要的機器零件在其設計中都包含了此類特徵。雖然角尖和邊緣通常會盡可能地倒圓,但裂縫仍然更容易在這些地方形成。將邊界兩側直接拉開的載荷最有可能擴充套件裂縫。因此,工程師必須特別注意這些位置以及作用在它們周圍的力,以確保物體在開始破裂之前能夠承受的最大應力不超過極限。
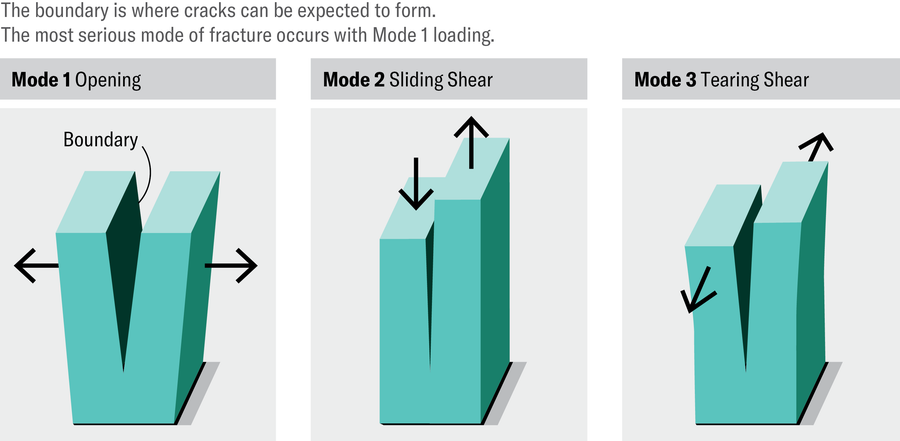
珍·克里斯蒂安森
為了做到這一點,他們需要找到在各種實際載荷下物體 PDE 的近似解。工程師有一種方便的技術來實現此目的,稱為有限元 (FE) 方法。在1956年一篇具有里程碑意義的論文中,工程師 M. 喬納森·特納、雷·W·克拉夫、哈羅德·O·馬丁和 L. J. 託普指出,為了理解物體如何變形,將物體視為由許多連線的部分組成(現在稱為有限元)會有所幫助。
假設您想找出當強大的風垂直吹襲二維彈性物體(例如沿其周邊固定的繃緊螢幕)時,該物體會如何變形。想象一下,用一堆連線的三角形面片代替螢幕,每個面片都可以移動和拉伸,但必須保持平坦的三角形。(也可以使用四邊形。)這種由三角形制成的模型螢幕與原始光滑螢幕不同,但它提供了一個更容易處理的問題。對於實際螢幕,您需要找到每個點的位移——這是一個無限的問題——對於由三角形制成的模型螢幕,您只需要找到每個三角形角的最終位置。這是一個有限的問題,相對容易解決,並且螢幕表面的所有其他位置都可以從其解中推匯出來。
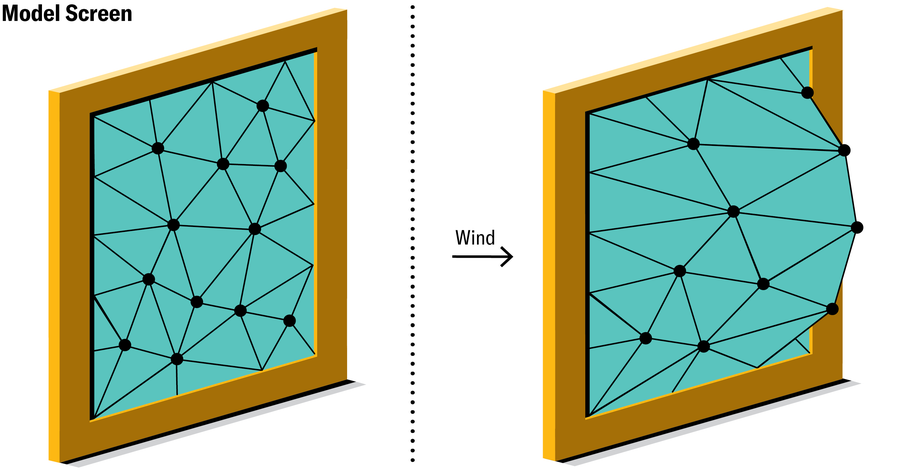
珍·克里斯蒂安森
物理學中的一個支配原則指出,螢幕將呈現出勢能最小的形狀,這是它因其位置或配置而擁有的能量。同樣的原則預測,吉他弦被撥動後,最終將恢復到直線形狀。該原則也適用於我們簡化的有限元螢幕,從而產生一組相對簡單的“線性”方程,用於求解節點處的未知位移。計算機非常擅長求解此類方程,並且可以告訴我們模型螢幕如何變形。
三維物體也可以類似地建模;對於這些物體,有限元通常是塊體或四面體,並且方程的數量通常要高得多。例如,對於整個飛機的建模,人們可能會預期一個具有數百萬個未知數的問題。
雖然有限元方法最初是為確定結構在受力時的行為而開發的,但該技術現在被視為求解 PDE 的通用方法,並且也用於許多其他領域。這些領域包括,例如,腫瘤學(跟蹤腫瘤生長)、製鞋業(實施生物力學設計)、電影動畫(使運動更逼真,如 2008 年的皮克斯電影機器人瓦力)和樂器設計(考慮振動的影響在樂器內部和周圍)。雖然有限元對於大多數人來說可能是一個陌生的概念,但人們很難找到一個我們的生活領域沒有它們發揮作用的地方。
一些應用涉及裂縫建模。例如,2018年研究的作者使用有限元來探索裂縫如何在牙齒中擴充套件以及哪種修復體可能最有效。在另一項研究中,科學家們研究了骨質疏鬆症可能導致不同年齡段的哪些型別的股骨骨折。有限元模擬還有助於在故障發生後揭示根本原因,例如佛羅里達州公寓倒塌和泰坦號內爆,並且在飛機事故後是常規操作。
憑藉他們積累的經驗,工程師理查德·H·麥克尼爾、約翰·A·斯旺森、佩德羅·V·馬卡爾和其他人在 20 世紀 70 年代釋出了幾個商業有限元程式碼。其中最著名的“傳統”程式碼最初是為 NASA 在 20 世紀 60 年代後期編寫的,現在被稱為開源 NASTRAN(“NASA 結構分析”的縮寫)。NASTRAN 仍然是航空設計關鍵步驟的首選程式,工程師在其中對正在設計的整個飛機的計算機模型進行粗略的有限元分析,以識別最有可能發生結構問題的區域和部件。然後對這些區域和部件進行更詳細的單獨分析,以確定它們將承受的最大應力以及裂縫可能在其中如何擴充套件。
諸如螺栓是否可能斷裂或風扇葉片是否可能斷裂等問題在單個部件層面上得到解答。幾乎所有此類區域性分析都涉及幾十年前推出的傳統程式,因為它們在商業環境中佔有很大的市場份額。我們乘坐的飛機或駕駛的汽車中最終使用的成品零件的設計在很大程度上取決於這些程式碼。工程師能夠從它們那裡獲得的答案有多準確?為了找出答案,我們需要深入研究數學。
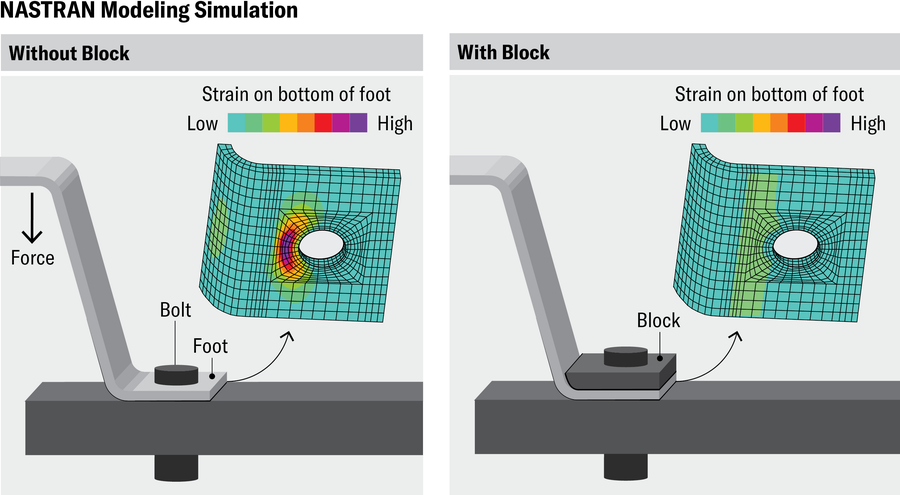
珍·克里斯蒂安森;來源:Robert J. Wingate 的“馬歇爾航天飛行中心用於研究太空梭外儲箱縱梁故障原因和糾正措施的應力分析和測試”,第 53 屆 AIAA/ASME/ASCE/AHS/ASC 結構、結構動力學和材料會議論文集,2012 年 4 月(參考文獻)
早些時候,我們瞭解瞭如何確定螢幕的有限元模型的變形,但是這個結果與真實變形有多接近呢?法國數學家讓·塞阿在他的 1964 年博士論文中首次提出的一個非凡定理,但根植於俄羅斯數學家鮑里斯·G·加勒金的工作,有助於回答這個問題。該定理指出,只要我們最大限度地減少勢能,在我們有限元螢幕可以呈現的所有可能變形中,透過我們的方法計算出的變形將是最接近 PDE 預測的精確答案的變形。
到 20 世紀 70 年代初期,世界各地的幾位數學家都使用塞阿定理來證明,隨著網格變得越來越精細,元素越來越小、數量越來越多,有限元模型的預測與真實形狀之間的差異將減小到零。數學家伊沃·巴布什卡和 A. 卡迪爾·阿齊茲(當時分別在馬里蘭大學學院公園分校和巴爾的摩縣分校)在 1972 年出版的具有里程碑意義的書中首次提出了統一的有限元理論,其中包含此定理和其他基本數學結果。
但在大約同一時間,數學家開始發現工程師正在將各種修改和“技巧”納入商業程式碼中,這些程式碼雖然經常違反能量最小化的關鍵特性,但在經驗上似乎是有效的。麻省理工學院的數學家吉爾伯特·斯特朗將此類修改命名為“變分犯罪”(“變分”來自變分法,變分法與有限元方法相關)。數學家可以證明,其中一些“犯罪”是良性的,但另一些則有可能產生明顯不正確的答案。
特別有問題的是用於處理稱為鎖定的精度下降的變通方法。當基本彈性方程包含一個接近無窮大的值時,就會出現此問題——例如,一個分母中使用極薄金屬板厚度的分數。鎖定也常發生在橡膠模型中,因為與胡克定律相關的彈性值變得非常大。直到 20 世紀 90 年代,巴布什卡和我才提供了鎖定的精確定義和表徵。到那時,其他幾位數學家,最著名的是義大利帕維亞大學的弗朗哥·佈雷齊,已經針對許多問題確定了哪些用於處理鎖定的變分犯罪是合理的,哪些應該避免,因為它們可能會給出不準確的答案。
但是,所有這些分析對傳統程式碼幾乎沒有影響,在傳統程式碼中,有風險的修改仍然存在。原因之一是,當數學家提出修改建議時,這些程式碼已經根深蒂固,因此將它們納入其中是不切實際的。此外,數學預測與實際實踐之間似乎存在差距——正如德克薩斯大學奧斯汀分校航空航天工程學教授托馬斯·J·R·休斯所說,“存在灰色地帶”。“一些在數學上可疑的修改在常見問題中可能比經過批准的修改表現更好。”
將更安全的鎖定解決方案納入其中的最大障礙也許是數學和工程學對有限元建模的不同看法。數學家將有限元解視為一系列近似值中的一個,在適當的數學條件下,這些近似值保證收斂到精確解。然而,在工程實踐中,有限元建模是一種獨立的設計工具,它可以告訴您實際建造的物體將如何表現。普通工程師通常最多在幾門課程中學習有限元,通常不會提及諸如問題修改之類的事情。休斯講述了一個軼事,一家建模公司拒絕購買較新的軟體產品,因為其結果與 NASTRAN 給出的答案不符。客戶堅持認為 NASTRAN 的解決方案是精確且正確的。(新軟體的設計人員只有透過逆向工程新軟體,才能使其產生的答案與 NASTRAN 的答案相匹配)
有限元解實際上可能與它們應該預測的物理結果大相徑庭。原因包括變分犯罪、基本數學模型的侷限性、模擬中排除較小的特徵以及使用有限問題代替求解 PDE 的無限問題。例如,大型飛機部件(如機身和機翼)的初步分析就是這種情況。工程師必須使用過去的實驗結果來“調整”有限元輸出,然後才能弄清楚真實的預測是什麼。這種積累的智慧對於解釋尚未經過物理測試的新設計的有限元結果至關重要。
較小零件(如耳片和緊韌體)的強度分析可能會帶來更多問題,因為通常沒有可用於調整事物的物理資料。一家大型航空航天公司向四個使用傳統程式碼的承包組織提出的 2022 年裂縫分析挑戰問題發現,三組的結果與真實的實驗確定解存在顯著差異。計算顯示裂縫的擴充套件速度比實際速度慢得多,導致預測的安全裕度令人不安地膨脹。
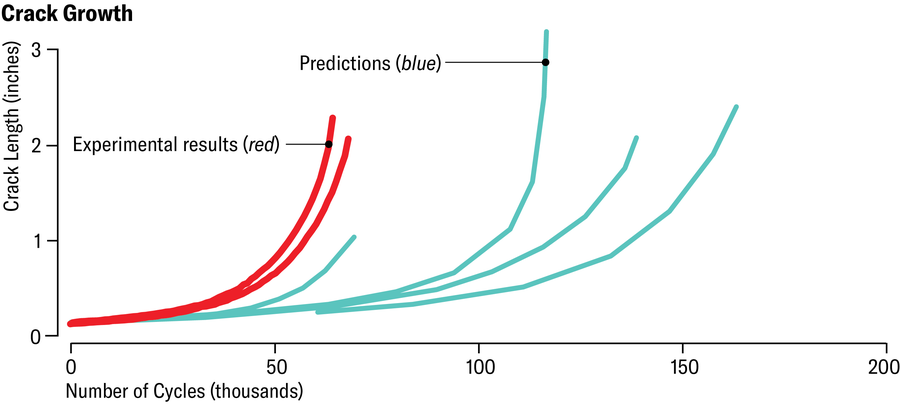
珍·克里斯蒂安森;來源:Barna Szabó 和 Ricardo Actis 的“應用科學中的劃界問題”,計算機與數學及其應用,第 1632 卷;2024 年 5 月(資料)
其他此類挑戰問題表明,不準確的程式碼不一定是核心問題——參與者通常會做出無效的簡化假設,或者從原始三角形和四邊形的眾多可用變體中選擇了錯誤的元素型別。此類錯誤可能會代價高昂:前面提到的 1991 年挪威石油平臺倒塌事件造成的損失按今天的美元計算超過 16 億美元。模擬缺陷也與F-35 戰鬥機的許多疲勞和裂縫問題有關,這些問題導致其成本嚴重超支和延誤。總的來說,對計算結果的確定性越小,就必須越頻繁地進行昂貴的檢查。
估計模擬的可靠性的問題似乎令人絕望。如果我們不知道飛機部件等計算機模型的精確解,我們如何才能衡量任何近似解中的誤差呢?但我們確實對解有所瞭解:它滿足物體的偏微分方程。我們無法求解 PDE,但我們可以使用它們來檢查候選解的效果——這是一個容易得多的問題。如果將未知的精確解代入 PDE,它將簡單地產生 0。近似解將產生餘數或“殘差”,通常稱為 R——衡量解的優劣的指標。
此外,由於物體是透過只能以某些方式變形的有限元建模的,因此計算出的應力不會像現實中那樣平滑地變化,而是在元素的邊界之間跳躍。這些跳躍也可以從近似解中計算出來。一旦我們計算出殘差和跳躍,我們就可以使用巴布什卡和匹茲堡大學的沃納·C·萊因博爾特以及其他數學家在 20 世紀 70 年代後期開始開發的技術來估計任何元素上的誤差。從那時起,也開發了其他策略來估計有限元分析的誤差。
估計誤差有幾個好處。首先,由於包含更小、數量更多的元素通常會提高精度,因此您可以對程式碼進行程式設計,使其在連續步驟中自動生成誤差可能很大的區域中的更小元素。我們已經從 PDE 的數學分析中看到,應力在角和邊緣附近增加得非常快。這種現象也使得這些區域的誤差最大。無需手動在這些關鍵位置建立更精細的網格,就可以自動完成此步驟。
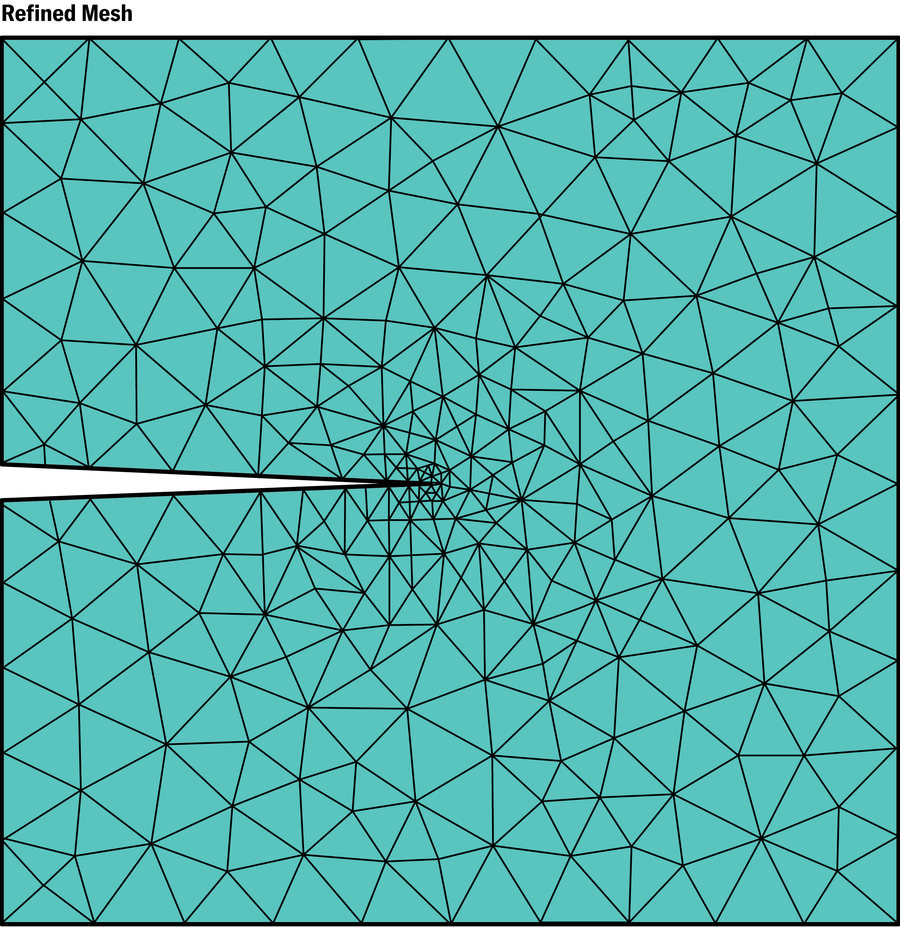
珍·克里斯蒂安森
其次,估計的總體誤差可以幫助工程師衡量他們感興趣的量的計算值的準確性,例如關鍵區域的應力強度或特定點的變形。工程師通常希望誤差在一定範圍內(從小於 2% 到 10%,具體取決於領域)。不幸的是,大多數演算法會高估或低估誤差,因此很難說它們提供的界限到底有多好。這方面仍然是一個活躍的研究領域。即便如此,如果使用誤差估計,幾乎肯定會提醒工程師注意他們挪威石油平臺有限元模型的問題。
估計總體誤差(即評估計算解的可靠性)的更好方法是使用有限元方法的不同理念:所謂的 p 細化,由聖路易斯華盛頓大學的工程師巴爾納·薩博在 20 世紀 70 年代首次開發。通常提高精度的方法稱為 h 細化,因為網格是透過減小典型元素的寬度(用 h 表示)來逐步細化的。對於 p 細化,我們始終堅持使用一個網格,但透過允許每個三角形以其他方式變形而不是始終保持平坦來提高精度。在第一步中,該方法允許任何三角形中的直線彎曲成拋物線,然後,逐步地,直線過渡到越來越複雜的曲線。這種修改為每個元素提供了越來越多的擺動空間,使其能夠在每個步驟中更好地匹配解的形狀。從數學上講,此過程相當於增加底層多項式的次數 p,即用於表示不同型別曲線的代數公式。
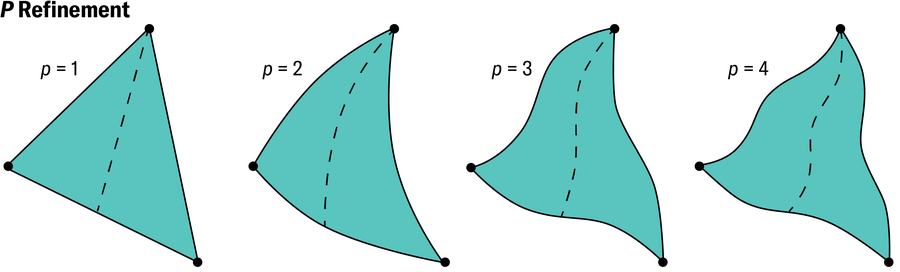
珍·克里斯蒂安森
正如巴布什卡和他的同事(包括我)所證明的那樣,對於廣泛的問題,p 細化比傳統的 h 方法更快地收斂到 PDE 的精確解。我還幫助從數學上證明了 p 版本沒有鎖定問題,因此不需要用於 h 方法的任何修改。此外,事實證明,一系列擺動形狀提供了一種簡單可靠的方法來評估可靠性。
然而,令人沮喪的是,評估可靠性的 p 方法和 h 方法都沒有在 20 世紀 70 年代至今使用的傳統程式碼中發揮重要作用。原因可能是這些程式是在這些進步出現之前設計和在文化上根深蒂固的。在較新的工業程式碼中,StressCheck 程式基於 p 版本,並且確實提供了可靠性估計。
當有實驗結果可供比較時,這種估計提供了進一步的好處:能夠評估物理現實與用於對其建模的 PDE 之間的差異。如果您知道有限元分析是準確的,但您的總體誤差仍然很大,那麼您可以開始使用更復雜的模型,例如那些基於比例不再成立的物理學的模型,以彌合差距。理想情況下,任何基礎數學模型都應透過與現實的此類比較來驗證。
人工智慧的出現很可能會改變計算機模擬的實踐。首先,模擬將變得更加廣泛可用。商業人工智慧程式的一個共同目標是“普及化”有限元建模,向可能在該領域幾乎沒有內在專業知識的使用者開放它。例如,自動化聊天機器人或虛擬助手可以幫助指導模擬。根據對此類助手進行培訓的徹底程度,它們可能是一種寶貴的資源,特別是對於新手工程師而言。在最佳情況下,助手將響應以普通語言提出的查詢,而不是需要技術性或格式化的措辭,並將幫助使用者從通常令人眼花繚亂的可用元素陣列中進行選擇,同時充分警惕在數學上可疑的修改。
人工智慧可以發揮作用的另一種方式是生成網格,當由人工使用者完成時,這可能會很昂貴,特別是對於角、裂縫尖端和其他特徵附近所需的精細網格。數學家已經確定了在二維和三維此類區域中設計網格的精確規則。這些規則可能極其難以手動輸入,但使用人工智慧應該相當容易。未來的程式碼應該能夠自動識別高應力區域並相應地劃分網格。
一項更初步的工作涉及完全取代有限元分析,而是使用機器學習來求解 PDE。這個想法大致是訓練一個神經網路來最小化殘差 R,從而構建一系列越來越精確的載荷位移預測。由於裂縫尖端附近存在高區域性應力,因此該方法在裂縫問題中的表現不佳,但研究人員發現,如果他們結合有關解的精確性質的資訊(例如,透過使用孔德拉季耶夫的數學工作),則該方法可能可行。
在這些以及其他可能改變遊戲規則的人工智慧舉措中,評估計算可靠性的這項絕對不起眼的任務(對於所有這些進步至關重要)尚未得到充分解決。利益相關者應參考 NASA 關於此類可靠性的要求。這些要求包括透過誤差估計和其他方式證明,基本物理學對於正在建模的現實生活情況是有效的,並且諸如有限元解之類的近似值在 PDE 的真實解的可接受範圍內。
NASA 最初將這些要求編纂成技術手冊,以應對哥倫比亞號太空梭災難。未來人類專業知識和監督減少的前景應該同樣是一個警鐘。如果我們要信任人工智慧提供的模擬結果,就需要內建可靠的可靠性保障措施。由於數學的進步,這些保障措施已經可用。我們需要將它們納入數值模擬的各個方面,以在日益具有挑戰性的世界中保持航空和其他工程事業的安全。

