“請來一杯健力士!”一位顧客對酒保說,酒保拿起一個印有商標的品脫杯,放在龍頭下接酒。酒保開始一個精確耗時 119.5 秒的多步驟傾倒過程,無論這是一種營銷噱頭還是酒精工程的奇蹟,都已經成為全球酒吧裡一種受人喜愛的儀式。結果:一杯濃郁的烈性黑啤酒,上面有一層完美的泡沫,就像一杯泥土味的奶昔。
自創始人亞瑟·健力士在都柏林簽訂了一份年租金 45 英鎊的 9000 年租約以來,健力士啤酒廠就以其創新方法而聞名。例如,在經過四年的嘗試後,一位從數學家轉行為釀酒師的邁克爾·愛德華·阿什發明了一種化學技術,使該啤酒廠的同名烈性黑啤酒具有天鵝絨般的泡沫。該方法包括向啤酒桶和健力士罐內的小球中新增氮氣,催生了當今非常流行的“氮氣冷萃”啤酒和咖啡風格。
但到目前為止,這家啤酒廠最具影響力的創新與啤酒無關。它是 t 檢驗的誕生地,t 檢驗是所有科學領域最重要的 統計技術 之一。當科學家宣佈他們的發現“具有統計顯著性”時,t 檢驗通常是這一結論的基礎。這是如何運作的?為什麼它會起源於啤酒釀造這種行業呢?
關於支援科學新聞業
如果您喜歡這篇文章,請考慮支援我們屢獲殊榮的新聞業,方式是 訂閱。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事能夠持續下去。
在 20 世紀初,健力士啤酒廠已經運營了近 150 年,並作為世界上最大的啤酒廠傲視群雄。在此之前,其產品的質量控制包括粗略的目測和氣味測試。但是,全球擴張的需求促使健力士的領導者改進他們的方法,以實現目標一致性和工業級嚴謹性。該公司聘請了一支智囊團,並賦予他們自由,讓他們可以為了釀造完美的啤酒而追求研究問題。這家啤酒廠成為實驗中心,以解答一系列問題:哪裡生長的大麥品種最好?麥芽提取物中理想的糖含量是多少?最新的廣告宣傳活動增加了多少銷量?
Shuyao Xiao
在蓬勃發展的科學活力中,該團隊面臨著一個持續存在的問題:如何在小樣本量的情況下解讀其資料。釀酒師面臨的一個挑戰涉及啤酒花,啤酒花是健力士啤酒的重要成分,它賦予啤酒苦味並充當天然防腐劑。為了評估啤酒花的質量,釀酒師測量植物的軟樹脂含量。假設他們認為 8% 是一個良好且典型的數值。但是,測試作物中的每一朵啤酒花在經濟上是不可行的。因此,他們做了任何優秀的科學家都會做的事情,並測試了啤酒花的隨機樣本。
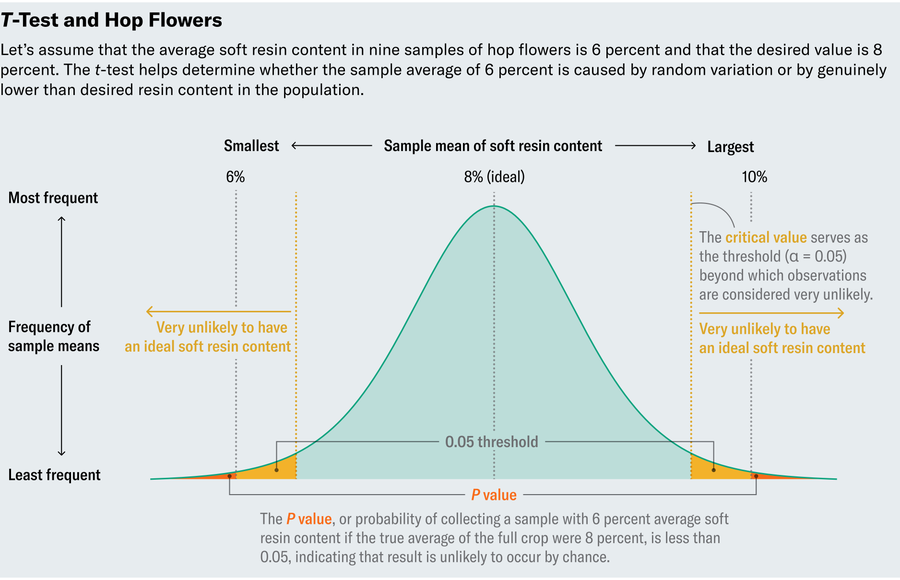
讓我們檢查一個虛構的例子。假設我們測量了九個樣本的軟樹脂含量,並且由於樣本各不相同,觀察到值的範圍從 4% 到 10% 不等,平均值為 6%——太低了。這是否意味著我們應該傾倒這批作物?不確定性來自對低值的兩種可能解釋。要麼這批作物的軟樹脂含量確實異常低,要麼即使樣本包含的量很低,但整個作物實際上很好。抽取隨機樣本的全部意義在於依靠它們作為整個作物的忠實代表,但也許我們很不幸地選擇了具有異常低水平的樣本。(畢竟我們只測試了九個樣本。)換句話說,我們應該認為樣本中的低樹脂含量與 8% 顯著不同,還是僅僅是自然的變異?
這個問題並非啤酒釀造獨有。相反,它滲透到所有科學探究中。假設在醫學試驗中,治療組和安慰劑組都有改善,但治療組的效果略好。這是否為推薦測試藥物提供了充分的理由?如果我告訴你這兩個組接受了兩種不同的安慰劑呢?您是否會傾向於得出結論,認為給予結果較好組的安慰劑一定具有藥用特性?或者可能是,當您跟蹤一群人時,他們中的一些人自然會好轉,有時會好轉一點,有時會好轉很多?同樣,這歸結為一個 統計顯著性 問題。
Shuyao Xiao
在健力士啤酒廠出現之前,特別是直到 20 世紀初健力士啤酒廠的首席實驗釀酒師威廉·西利·戈塞特發明了 t 檢驗,關於小 樣本量 領域中這些長期存在的問題的理論才得以發展。統計顯著性的概念早於戈塞特,但之前的統計學家是在大樣本量的情況下工作的。要理解為什麼這種區別很重要,我們需要了解如何確定統計顯著性。
請記住,在我們的假設場景中,啤酒花樣本的平均軟樹脂含量為 6%,我們想知道整個作物的平均值實際上是否與期望的 8% 不同,或者我們只是樣本運氣不好。因此,我們將問一個問題:如果整個作物是典型的(平均值為 8%),那麼我們觀察到如此極端值(6%)的 機率 是多少?傳統上,如果這個機率(稱為 P 值)小於 5% 或 0.05,那麼我們就認為這種偏差具有統計顯著性,儘管不同的應用需要不同的閾值。
通常,兩個獨立的因素會影響 P 值:樣本偏離總體預期值的程度以及大偏差的常見程度。可以將其視為訊號與噪聲之間的拉鋸戰。我們觀察到的均值(6%)與我們期望的均值(8%)之間的差異提供了訊號——這種差異越大,作物真正具有低軟樹脂含量的可能性就越大。花朵之間的標準差帶來了噪聲。標準差衡量資料在均值周圍的離散程度;小值表示資料在均值附近波動,而大值表示更大的變異。如果軟樹脂含量通常在芽之間波動很大(也就是說,如果它具有較高的標準差),那麼也許我們樣本中的 6% 平均值不應該讓我們擔心。但是,如果花朵傾向於表現出一致性(或較低的標準差),那麼 6% 可能表明與期望的 8% 存在真正的偏差。
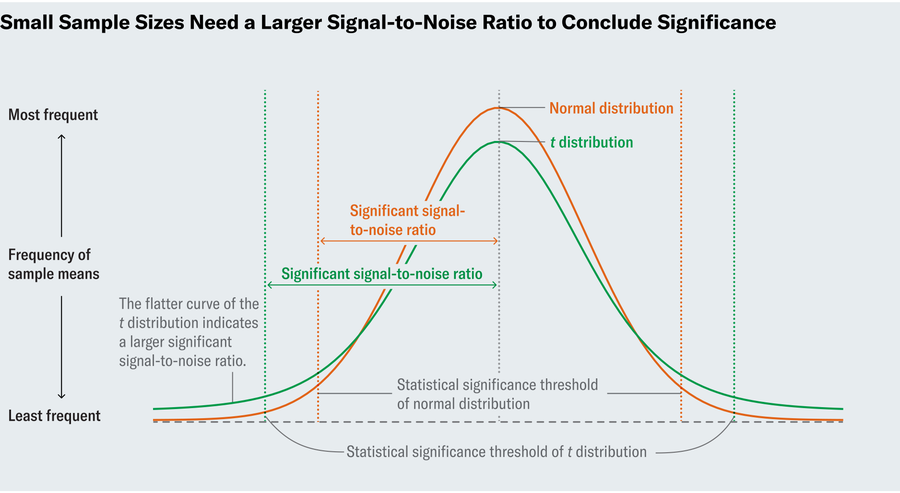
為了在理想世界中確定 P 值,我們將首先計算信噪比。該比率越高,我們對研究結果的顯著性就越有信心,因為高比率表明我們發現了真正的偏差。但是,什麼才算是高信噪比呢?為了認為 6% 與 8% 顯著不同,我們特別想知道信噪比何時如此之高,以至於在樹脂含量為 8% 是常態的世界中,只有 5% 的可能性發生這種情況。戈塞特時代的統計學家知道,如果您多次執行實驗,計算每次實驗中的信噪比並繪製結果圖,則該圖將類似於“標準正態分佈”——熟悉的正態分佈曲線。由於正態分佈是眾所周知的且有充分記錄的,因此您可以在表格中查詢比率必須有多大才能達到 5% 的閾值(或任何其他閾值)。
戈塞特認識到,這種方法僅適用於大樣本量;小啤酒花樣本不能保證正態分佈。因此,他一絲不苟地為較小的樣本量製表了新的分佈。現在稱為 t 分佈,這些圖類似於正態分佈,因為它們是鐘形的,但鐘形曲線的下降程度不如正態分佈那麼劇烈。這意味著需要更大的信噪比才能得出顯著性結論。他的 t 檢驗使我們能夠在以前人們無法進行推斷的情況下進行推斷。
2008 年,數學顧問約翰·D·庫克在他的 部落格 中思考,也許 t 檢驗起源於啤酒廠而不是葡萄酒廠不應該讓我們感到驚訝。啤酒廠要求其產品的質量保持一致,而釀酒師則陶醉於多樣性。葡萄酒有“好年份”,每瓶酒都有一個故事,但您希望每一杯健力士啤酒都能提供相同的標誌性口味。在這種情況下,統一性激發了創新。
戈塞特用他的新技術解決了啤酒廠的許多問題。這位自學成才的統計學家以筆名“Student”發表了他的 t 檢驗,因為健力士不想向競爭對手洩露其研究成果。儘管戈塞特開創了工業質量控制,併為定量研究貢獻了大量其他想法,但大多數教科書仍然稱他的偉大成就為“Student’s t-test”(學生 t 檢驗)。歷史可能忽略了他的名字,但他可以自豪的是,t 檢驗是迄今為止科學界最廣泛使用的統計工具之一。也許他的成就應該被載入《吉尼斯世界紀錄大全》(這個想法是健力士啤酒廠的總經理在 20 世紀 50 年代構想出來的)。為此乾杯。
