在明星雲集的懸疑驚悚片《靈數23》於2007年在電影院上映後,許多人開始確信他們在任何地方都能看到這個同名數字。那時我還在上學,我的一些同學每當數字23出現在任何語境中都會不寒而慄。其他人則對這種形式的命理學著迷,因為一旦你更多地關注某個事物——包括一個數字——你就會感覺你看到它的頻率太高了,不可能是純粹的巧合。
長期以來,人們一直認為已故數學家約翰·麥凱可能也成為了這種被稱為“頻率錯覺”或巴德爾-邁因霍夫現象的受害者。在麥凱的案例中,抓住他想象力的數字是196,884。
像23這樣的兩位數反覆出現似乎並不太令人驚訝。但是一個六位數的數字也會這樣做嗎?麥凱在1978年偶然發現了這個數字,當時他正在翻閱一篇數學領域的論文,而這個領域並不是他的專長。他研究的是幾何學,研究的是圖形的對稱性。然而,那天,他正在檢視來自數論的結果,數論是研究整數的性質的,例如素數。他偶然發現了一個以值196,884開頭的數字序列。
支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們今天世界的發現和想法的具有影響力的故事。
這個數字聽起來麥凱很熟悉。他之前研究過一種數學結構——當時仍然是假設性的——被稱為“怪獸”。這種奇怪的代數結構旨在描述一個生活在196,883維空間(僅比數字196,884少一維)中的幾何物體的對稱性。而且由於一維點無論如何都滿足每個對稱性,因此怪獸也可以描述其對稱性質。因此,麥凱以一種非凡的方式再次發現了數字196,884。他將數學家認為怪獸對稱性適用的前兩個維度相加:196,883 + 1 = 196,884。
這聽起來牽強附會嗎?其他人也這麼認為。專家們對麥凱的結果幾乎沒有關注。畢竟,像怪獸這樣的結構包含許多數字,麥凱與之相關的數論結果也是如此。“如果你有很多數字,那麼其中一些數字會大致相同,這只是巧合,”數學家理查德·博切茲說,他在該領域做出了重大貢獻,在一個解釋性的YouTube影片中。
但是麥凱無法擺脫幾何學和數論這兩個截然不同的數學領域可能存在聯絡的感覺。據報道,他甚至在會議上穿著印有“196,883 + 1 = 196,884”字樣的T恤。
完全瘋狂還是天才之舉?
不久之後,數學家約翰·湯普森意識到麥凱的懷疑可能並非毫無道理。他成功地將物體遵循怪獸對稱性的下一個更高維度與數論中神秘數字序列的下一個成員聯絡起來。維度是21,296,876。這些值有所不同——但是如果你像以前一樣將所有怪獸維度加起來(1 + 196,883 + 21,296,876),結果是21,493,760。
這令人驚訝,因為你可能還記得,當麥凱第一次發現196,884時,他正在檢視數論中的一個特殊序列。該序列中的第二個數字是21,493,760——湯普森的結果。換句話說,看起來兩個看似無關的數學領域之間真的可能存在聯絡。
此時,數學界開始感到好奇。也許麥凱畢竟是對的——即使這聽起來完全荒謬。這種描述難以想象的物體的對稱性並且甚至尚未完全構建的奇怪結構,與數論有什麼關係呢?
到1979年,越來越多的證據表明,其他數字和維度似乎也遵循這種出乎意料的模式。數學家約翰·康威和西蒙·諾頓最終發表了一篇題為“怪獸月光”的論文,其中他們提出了幾何學和數論之間存在聯絡的猜想。“他們稱之為月光,因為它看起來太牽強了,”德國波恩馬克斯·普朗克數學研究所的數論家唐·扎吉爾在2015年對Quanta Magazine說。
事實上,證明這個月光猜想可能幾乎沒有希望。除了這兩個遙遠的數學領域是否有關聯尚不清楚之外,甚至怪獸是否真的存在也完全不清楚。
月光下的怪獸
怪獸是群論的理論預測,群論是幾何學的一個分支,處理物體的對稱性質。在20世紀70年代,數學家開始建立一種群的元素週期表:他們想找到有限對稱性的“原子”。根據這種思維方式,每個有限群都可以用這些原子的組合來表示。經過數十年的研究,幾何學家似乎終於達到了他們的目標。與化學元素不同,存在無限多的“有限單群”,但幾乎所有群都可以分為18類,其排列方式讓人聯想到元素週期表。此外,專家們總共發現了26個不屬於這18類的外來者。
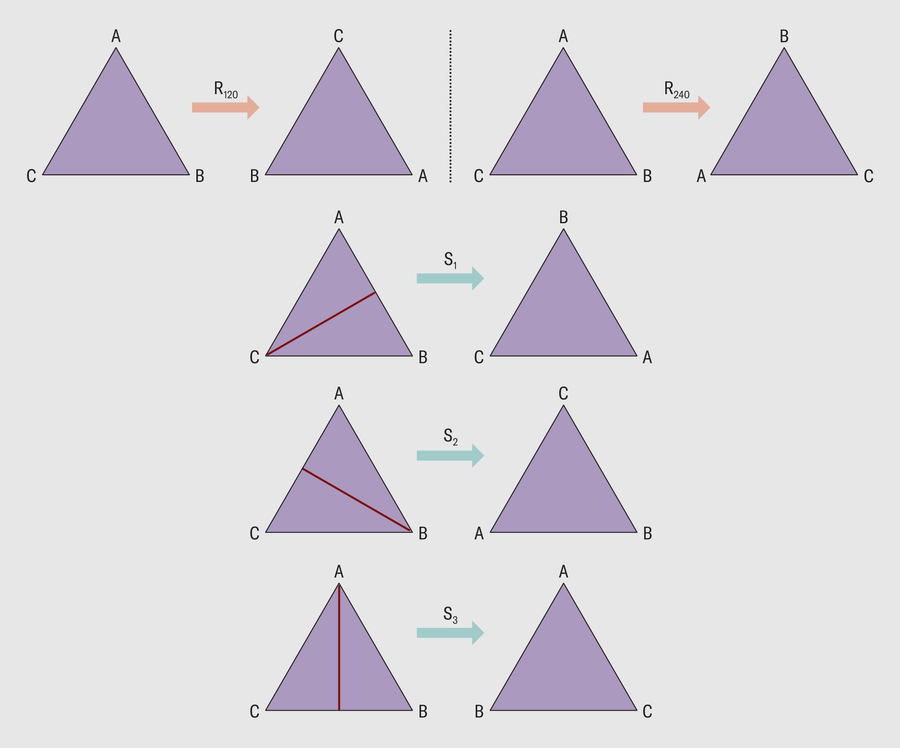
三角形的對稱性形成一個有限群。圖片來源:Spektrum der Wissenschaft/馬農·比肖夫,阿曼達·蒙塔內斯重新設計
這些離群值中的第一個是“怪獸”,數學家伯恩德·費舍爾和羅伯特·格里斯在1973年預測了它。這個名字來源於這個群的龐大規模:它包含超過8 x 1053個對稱性。作為比較,一個20面“D20”骰子(一個二十面體)的對稱群包含60個對稱性,這意味著可以進行60種可能的變換(旋轉或反射)而不會改變D20的方向。
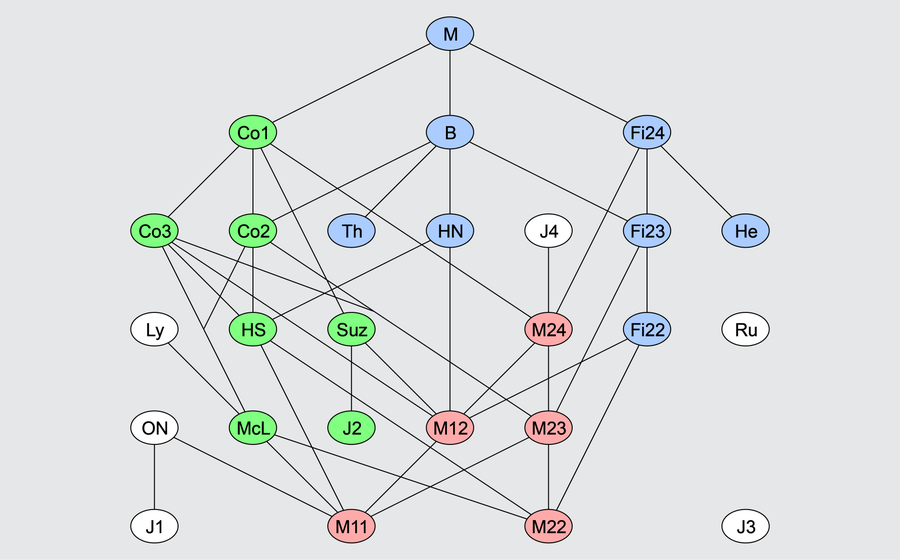
一些紅色、綠色和藍色的零星群彼此相關。白色的零星群被認為是外來者。圖片來源:Drschawrz/Wikimedia Commons(CC BY-SA 3.0)
由於其龐大的規模,怪獸給數學家帶來了巨大的挑戰。“大多數人認為構建它將是毫無希望的,因為當時即使是小得多的群也需要計算機構建,”博切茲在他的YouTube影片中解釋道。與此同時,即使是功能強大的計算機也難以處理由8 x 1053個元素組成的結構。
然而,這種悲觀的預測最終被證明是錯誤的。1980年,格里斯構建了怪獸,從而證明了它的存在——沒有藉助計算機的幫助。
類固醇上的正弦函式
數論主要研究整數,乍一看似乎很簡單。但是為了研究它們之間的關係,專家們求助於複雜的概念,例如所謂的模形式。這些是函式f(z),它們非常對稱。與正弦函式一樣,你只需要知道模形式的特定部分就可以知道它在其他任何地方的樣子。
“模形式有點像三角函式,但加了類固醇,”數學家肯·小野告訴QuantaMagazine。
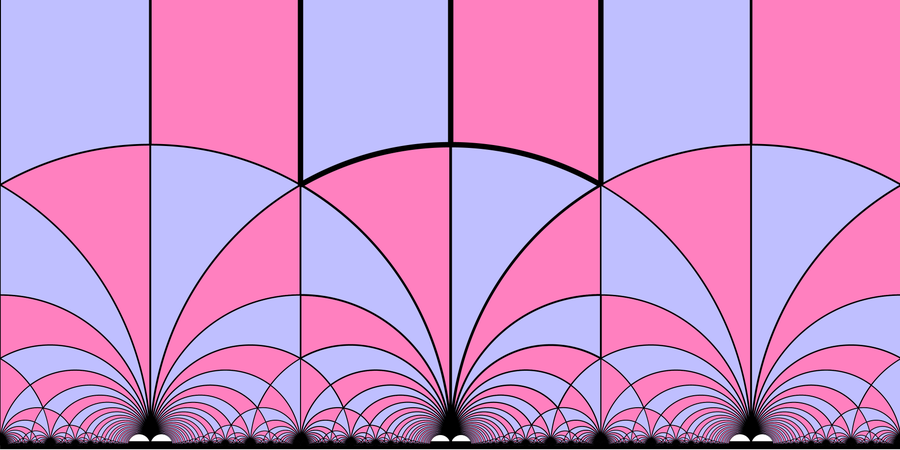
彩色模形式包括模空間,如圖所示,模空間是一個幾何空間,其點對應於固定的代數幾何物件。圖片來源:Neozhaoliang/Wikimedia Commons(CC BY-SA 4.0)
儘管如此,它們在數學中起著極其重要的作用。例如,牛津大學的安德魯·懷爾斯使用它們來證明費馬大定理,而瑞士洛桑聯邦理工學院的瑪麗娜·維亞佐夫斯卡使用它們來尋找八個空間維度中最密集的球體堆積排列。然而,由於模形式非常複雜,它們通常用無限長的多項式來近似,例如
f(q) = (1⁄q) + 744 + 19,688q + 21,493,760q2 + 864,299,970q3 + …
變數q前面的前因子形成一個從數論角度來看具有有趣性質的數字序列。麥凱將這個數字序列與怪獸聯絡起來。
一個令人驚訝的聯絡
博切茲在20世紀80年代首次聽說了月光猜想。“我當時完全被它震驚了,”他在接受YouTuber Curt Jaimungal的採訪時回憶道。博切茲當時正在康威的一次講座中,瞭解到數論和群論可能存在神秘的聯絡。這個主題從未讓他釋懷。他開始尋找可疑的聯絡,直到他找到了它。1992年,他發表了他的突破性成果,並因此在六年後的1998年獲得了菲爾茲獎,這是數學領域的最高獎項之一。他的結論是:一個高度投機的物理學領域,弦理論,可以為怪獸和數字序列之間缺失的拼圖提供答案。
弦理論試圖統一物理學的四種基本力(電磁力、強核力、弱核力和引力)。與傳統理論中依賴粒子或波來構成宇宙的基本組成部分不同,弦理論涉及一維結構:微小的線狀物像樂器的弦一樣振動,從而產生我們在宇宙中感知到的熟悉的粒子和相互作用。
博切茲知道弦理論是基於許多與對稱性相關的數學原理的。事實證明,模量也起著作用。當微小的線狀物閉合並在時空中以擺動的方式移動時,它們的軌跡形成一個二維管。無論線狀物如何振盪,這種結構都具有與模形式相同的對稱性。
博切茲研究的那種弦理論只能在25個空間維度中進行數學公式化。然而,由於我們的世界僅由三個可見的空間維度組成,因此弦理論家假設其餘22個維度捲曲成微小的球體或甜甜圈狀的環面。但是物理學取決於它們的精確形狀:維度捲曲成圓柱體的弦理論提供的預測與維度形成球體的弦理論提供的預測不同。為了以適合我們世界的方式描述粒子及其相互作用,物理學家必須在他們的計算中找到正確的“緊緻化”。
博切茲將24個維度捲曲成一個24維的甜甜圈表面,並發現相關的弦理論具有怪獸的對稱性。只剩下一個自由空間維度並沒有困擾他。畢竟,他對模型的數學性質感興趣,而不是對描述我們世界的物理理論感興趣。
在這個構建的世界中,線狀物沿著24維的甜甜圈擺動。怪獸的維度計算了線狀物在特定能量下可以振動的所有方式。因此,在最低能量下,它僅以一種方式振動;在下一個最高能量下,已經有196,883種不同的可能性。並且線狀物留下的軌跡具有模形式的對稱性。
博切茲因此證明了怪獸群和模形式之間的聯絡。而且這不會是唯一的這種情況:與此同時,數學家們已經能夠將其他有限群與其他模形式聯絡起來——在那裡,弦理論也提供了聯絡。因此,即使事實證明這種投機理論不適合描述我們的宇宙,它仍然可以幫助我們發現全新的數學世界。
本文最初發表於Spektrum der Wissenschaft,經許可轉載。
