Benjamin Adric Dunn,挪威科技大學的資料科學家,向我展示了一張排列不均勻的點圖,模糊地像巨石陣的岩石。 總體模式很清晰——至少對人類來說是這樣。“當我們看這個時,很明顯這是一個圓圈,”他說。 但演算法很可能難以識別這個簡單的形狀。“它經常忽略大局。”
許多科學過程都涉及迴圈或重複。 計算機無法看到這些關係對於想要在大量資料點中識別迴圈模式的科學家來說是一個問題。 資料通常被視覺化為漂浮在空間中的點,就像夜空中的星星一樣。 一個點可能代表一個物理位置,例如標記船舶在公海位置的經度和緯度兩個數字。 基因同樣可以繪製在許多維度的數學空間中——有時是數百個維度——這樣,具有相似 DNA 序列的兩個基因將由附近的點表示。 資料中迴圈模式的意義取決於上下文。 船舶位置中的圓圈可能表明它迷路了,而遺傳資料中的圓圈可能證明進化關係。
通常,這些資料點的星空過於複雜和高維,無法用肉眼研究。 為了檢測圓圈,研究人員需要一套足夠精確的指令,以便計算機能夠理解。 但是,許多標準的資料分析技術都基於一種稱為線性代數的數學型別,它研究直線和平坦平面。 為了找出迴圈,研究人員轉而使用拓撲資料分析 (TDA),這提供了一種完全不同的視角。
與表徵線性代數的相對簡單和剛性的結構相比,TDA 以拓撲學為基礎,拓撲學是數學的一個分支,研究柔韌的、可拉伸的形狀。 因為它的從業者假設所有形狀都是任意靈活的,所以拓撲學通常被稱為橡皮泥幾何學。
就像從星星形成星座一樣,拓撲資料分析幫助數學家從分散的點構建揭示性的形狀。 研究人員首先將資料點用作虛擬支架中的節點或關節,構建可能延伸到數百維度的複雜結構。 由此產生的圖片包含原始資料的大部分本質,但以更具體的形式呈現。 他們使用拓撲視角研究這些結構——尋找即使支架被拉伸或彎曲也能保留的特徵。
拓撲學在資料分析中的用處在於它能夠揭示定性而非定量的屬性。 它識別結構的各個方面,即使在底層測量中存在隨機誤差或噪聲,這些方面仍然存在。 噪聲通常會抖動底層資料,但拓撲結構保持不變——揭示系統的穩健特徵。“在現實世界中,有很多例項給你的資料是軟綿綿的,”賓夕法尼亞大學的數學家羅伯特·格里斯特說。“所以你必須使用軟綿綿的數學。”
數學家和科學家現在正在共同努力,在大量資料中尋找不尋常的拓撲形狀,這些資料代表從具有日常節律的生物過程到藥物分子的結構等任何事物。 也許這些研究中最有趣的是關於大腦結構的。 數學家已經使用拓撲學來探索神經元如何在整個大腦的擴充套件區域相互作用,對不同的環境和刺激做出反應。 最近,鄧恩與神經科學家合作發現,某些腦細胞使用環面(甜甜圈表面的數學名稱)來繪製其環境圖。

圖片來源:Jen Christiansen
甜甜圈和咖啡杯
即使拓撲學家以扭曲橡皮泥為生,他們也非常小心地保持其中的孔洞數量。 他們從不打出新孔或壓閉現有孔。 有一個經典的數學笑話,拓撲學家無法區分甜甜圈和咖啡杯:它們都有一個孔。
拓撲學家根據孔的維度對孔進行分類。 閉環,如數字 0,有一個一維孔,因為它是由將一維線的兩端粘合在一起形成的。 從二維平面(如一張紙)開始,並粘起邊緣將產生類似空心球的東西,它有一個二維孔。
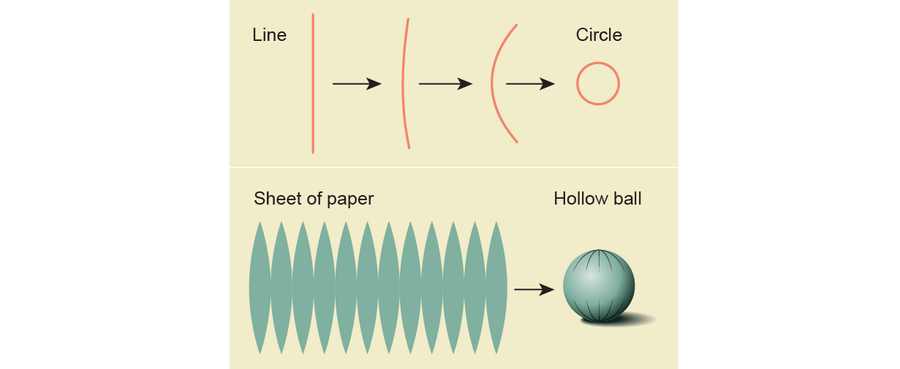
圖片來源:Jen Christiansen
更高維度的形狀可以有更高維度的孔。 透過類比一維和二維孔,例如,三維孔是透過“封閉”三維空間(如立方體)形成的。 但是這個過程只能從四維視角來看,超出大多數人——可能任何人的——理解範圍。
有些形狀有多個不同維度的孔,例如帶有附加把手的充氣球,孩子可以坐在上面彈跳。 球的空心中心是一個二維孔,而實心把手形成一個一維孔。 拓撲學有許多精確的方法來計算更高維度形狀中的孔洞——這種能力被證明有助於研究大腦的神經元活動。
印第安納大學的神經科學家奧拉夫·斯波恩斯將大腦視為一個龐大的交通網路。 道路和基礎設施由神經元及其連線的突觸構成。 大腦的電訊號和化學訊號沿著這些街道驅動。“物理道路限制了你可以在頂層動態觀察到的交通模式,”斯波恩斯說。 當我們移動和思考時,交通模式會發生變化。
當我們眯著眼睛看大腦的圖表時,它可能看起來像點的集合,代表神經元。 其中一些點由線條連線,表示這些特定神經元之間的突觸。 數學家將這種結構稱為圖:由邊連線的節點的集合。 圖使大腦的生物複雜性變得扁平,但它保留了電路的整體形狀。 這種權衡在建立數學模型時很典型,數學模型權衡簡單性和可分析性與實用性。
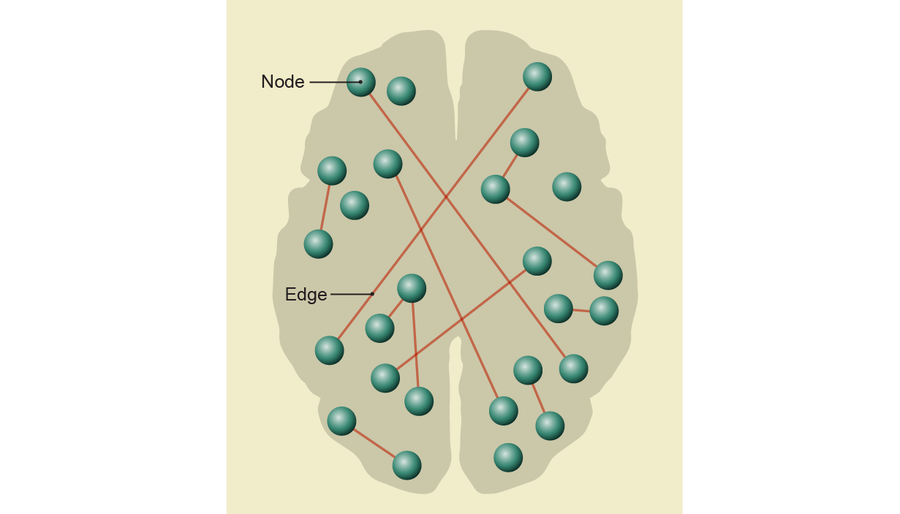
圖片來源:Jen Christiansen
神經元連線圖是一個網狀結構:神經元豐富且相互交織。 2017 年,洛桑瑞士聯邦理工學院的數學家凱瑟琳·赫斯透過做一件最初令人驚訝的事情來解決這種複雜性:她使圖變得更加複雜。 她分析了來自藍腦計劃的資料,這是一個大規模計算機模擬齧齒動物新皮層活動的專案,新皮層是大腦中參與高階功能的部分。 該計算機模型包含單個神經元的表示,這些神經元透過突觸連線到其他模擬神經元。 這些連線以及它們何時可能放電由基本的生物學原理和來自實驗室齧齒動物的實驗資料決定。
該模擬可以顯示大腦的交通模式——神經元響應刺激而放電。 然而,與真實大腦的鳥瞰圖不同,模擬可以暫停,讓科學家看到凍結幀,顯示哪些突觸正在響應給定的刺激而放電。 將此靜態影像轉換為圖很容易,因為它指示了資料點以及它們之間的線條:如果連線它們的突觸正在放電,則兩個神經元是連線的。 從這張圖中,赫斯構建了數學家稱之為單純復形的東西,將簡單的圖轉換為體積龐大的形狀。
單純復形由不同維度的三角形構成。 例如,在藍腦圖中,三個神經元,它們之間所有三個突觸都傳輸訊號,形成了空心三角形的頂點。 為了將這種結構擴充套件為單純復形,數學家們用實心的二維三角形填充了這個空心三角形。 同樣,他們用更高維度的三角形類似物填充了更大的連線神經元簇。 例如,四面體(一個帶有四個三角形面的實心三維金字塔)將填充一組四個同時放電的神經元。
赫斯和其他人觀察到的作為一組放電的神經元的最大數量是八個,因此這個單純復形的最大部分是一個七維三角形。 許多元素重疊,形成一個多維雕塑:一個三角形可能從四面體中突出,並在一個點與另一個三角形相遇。 此外,數學家和科學家不僅檢查了一個,而且檢查了一系列凍結幀,這些幀是在模擬輕輕撫摸齧齒動物的鬍鬚後拍攝的。 他們將這些地圖中的每一個都轉換為一個單純復形,並使用拓撲學工具分析其形狀如何隨時間變化。
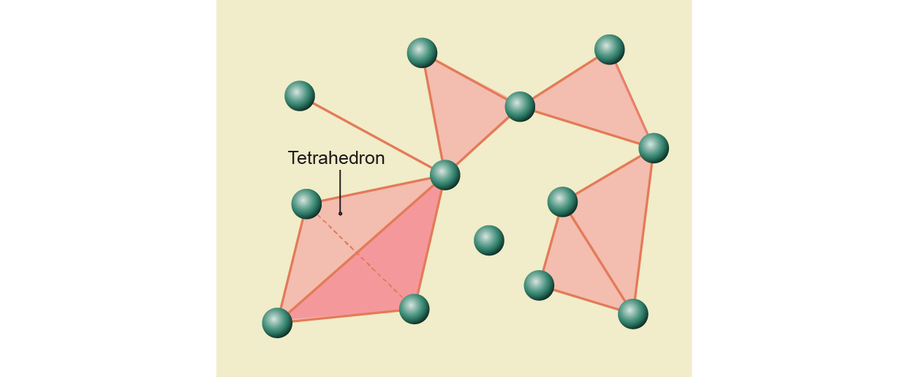
圖片來源:Jen Christiansen
在接收到刺激後,單純復形立即像一個巨大的樂高積木結構一樣增長,新增更高維度的碎片,直到雕塑達到最大三維或四維,具體取決於刺激。 然後整個東西迅速消失。“你有這些越來越複雜的結構,它們是由刺激建立的,直到它完全崩潰,”赫斯說。
對於拓撲學家來說,連線成三角形的三條線與空心圓相同,因為一種形狀可以彎曲成另一種形狀。 因為赫斯和她的同事從模擬齧齒動物大腦構建的單純復形是七維的,所以它們可以有多達七個維度的孔。 他們的分析表明,隨著形狀的增長,孔的數量也在增加。 在其峰值時,該結構包含驚人數量的二維和三維孔——比隨機單純復形或從不同生物過程構建的單純復形產生的孔多得多。 孔的特定模式揭示了神經元反應的高度組織性;這種複雜性可能表明思維過程的基本特徵。
頑固的孔
然而,更常見的情況是,資料由漂浮在抽象數學空間中的孤立點表示,沒有明顯的、預先確定的連線。 為了應用 TDA,數學家需要弄清楚如何連線它們。 但是有很多可能的方式將星星連線成星座。 為了找到這些隱含的圖畫,數學家使用一種稱為持久同調的技術。 拓撲學家分析以各種尺度構建的一系列單純復形,以找到資料雲的基本特徵。
為了製作第一個單純復形,他們儘可能廣泛地撒網,將每個點連線到每個其他點以形成密集的網格。 用固體形式填充這個網路會產生一個高維單純復形,幾乎沒有明顯的特徵。 但是數學家需要將這個復形與透過在較小尺度連線資料而形成的其他復形進行比較。 因此,接下來,他們在相同的資料上撒下更窄的網,僅連線附近的點。 現在他們有了一個更稀疏的網路,他們用它來構建第二個單純復形。 因為這個網格包含的資料點較少,所以它的單純復形包含較低維度的形狀。 研究人員使用一系列更小的網重複該過程。“在每個尺度上,你都會得到該復形外觀的不同快照,”俄亥俄州立大學的數學家蘭索尼·埃德蒙茲說。
每個單純復形都是用相同的分散資料點形成的可能星座。 拓撲學家研究這種形狀譜——特別是記錄每個維度中孔的數量。 他們對在許多不同尺度上持續存在的孔特別感興趣。 有些孔短暫出現然後消失,但頑固的孔——那些在一定尺度範圍內倖存下來的孔——指向資料的最基本特徵。 因此,TDA 可以將複雜的資料混亂簡化為頑固孔的簡單列表,這與 JPEG 照片檔案壓縮影像的方式非常相似。“這是一種將資料精簡為真正重要的東西的方式,以便我們擁有更實用的東西,”格里斯特說。
有時,以這種方式識別的孔具有直接的解釋。 東北大學的數學家何塞·佩雷亞和一組計算生物學家使用持久同調來尋找週期性生物過程——那些以有規律的間隔重複的過程。 例子包括酵母的代謝週期或小鼠的晝夜節律。“什麼是復發或重複?”佩雷亞問道。“從幾何角度來看,它應該像你在你正在觀察的事物的空間中遍歷某種迴圈。”
TDA 還幫助研究人員設計新藥。 這些化合物通常是透過調整現有藥物的分子結構來發現的。 但是分子的結構極其複雜且難以分析,即使對於機器學習演算法也是如此。 為了設計新藥,計算機需要使用現有分子的簡化表示。 有許多方法可以做到這一點,但密歇根州立大學的魏國偉領導的團隊選擇將分子簡化為它們的“拓撲簽名”。 這是基於其拓撲特徵對化學物質的描述——本質上是透過持久同調獲得的資訊集合,例如每個維度中頑固孔的數量。
大腦迴圈
TDA 最有趣的應用可能是在大腦組織的最基本層面——單一型別的神經元。 2014 年,約翰·奧基夫和研究夥伴梅-布里特·莫澤和愛德華·莫澤因發現位置細胞和網格細胞(分別是在動物位於特定位置時啟用的神經元型別)而獲得諾貝爾醫學獎。 賓夕法尼亞州立大學的數學家卡琳娜·庫爾託說,它們充當位置感測器。
當大鼠在其環境中的多個位置時,其大腦中的每個網格細胞都會亮起。 為了弄清楚網格細胞與大鼠位置之間的關係,神經科學家選擇了一個網格細胞進行研究。 他們在地板的計算機模型上畫了一個點,標記大鼠每次啟用該細胞的位置。 隨著大鼠在方形盒子中自由移動,出現了一種規則且重複的點模式,數學家將其描述為六邊形晶格。 晶格上的點代表該特定網格細胞亮起的所有位置。 他們對多個網格細胞重複了這個過程,用不同的顏色標記每個網格細胞。 與每個網格細胞對應的點具有相同的整體幾何圖案,但彼此偏移,像繁忙的瓷磚一樣覆蓋盒子。
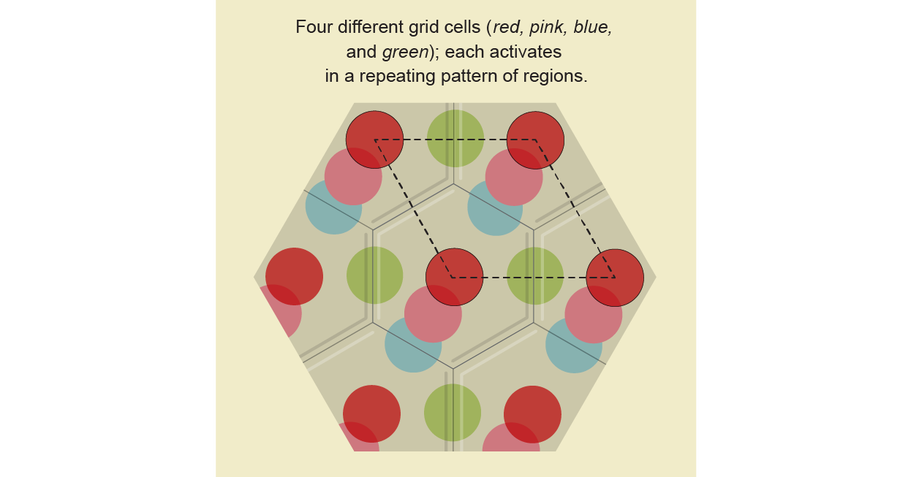
圖片來源:Jen Christiansen;來源:Carina Curto 在《美國數學會通報》第 54 卷第 1 期中發表的“拓撲學能告訴我們關於神經程式碼什麼?”;2017 年 1 月(參考文獻)
神經科學家想準確瞭解網格細胞如何表示空間位置——本質上,他們正在尋找產生六邊形圖案的模板。 例如,想象一個圓形橡皮圖章,上面印有各種卡通人物。 當您展開圖章時,它將建立一條線。 米老鼠的影像將沿線以規則的間隔出現。 但所有這些影像都來自原始橡皮圖章上的同一位置。 很容易想象展開圖章,但反向問題更具挑戰性:如何從它建立的圖案中生成模板圖章?
在代表每個網格細胞放電時大鼠所在位置的彩色點平鋪中,四個相鄰的紅點形成了傾斜矩形的角,該矩形稱為平行四邊形。 就像重複的米老鼠影像一樣,所有相同顏色的紅點都對應於單個網格細胞。 因此,拓撲學家識別出所有紅點,使用他們稱為“粘合”的操作將平行四邊形摺疊成甜甜圈形狀。 首先,他們將平行四邊形的兩條相對邊粘合在一起,形成一個帶有兩個紅點的圓柱體:一個在頂部,一個在底部。 接下來,他們彎曲圓柱體,將兩端粘合在一起形成環面。 這樣,平行四邊形的四個紅色角就變成了甜甜圈上的一個點。 每種其他顏色的點正好會在環面上顯示一個。 因此,就像圓形圖章是卡通線條的模板一樣,環面是網格細胞如何表示盒子地板的正確地圖。
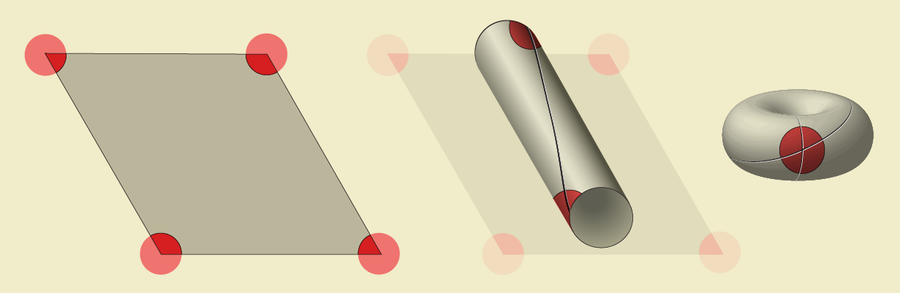
圖片來源:Jen Christiansen
當大鼠在盒子周圍跑動時,神經科學家可以看到這種模式。 但是,當大鼠在其他測試場地(例如帶有輪輻和中心輪轂的腳踏車輪)周圍移動時,更難以視覺化該模式。 每個網格細胞仍然在多個位置放電,但科學家對底層地圖沒有信心。 點的排列結構不明顯。
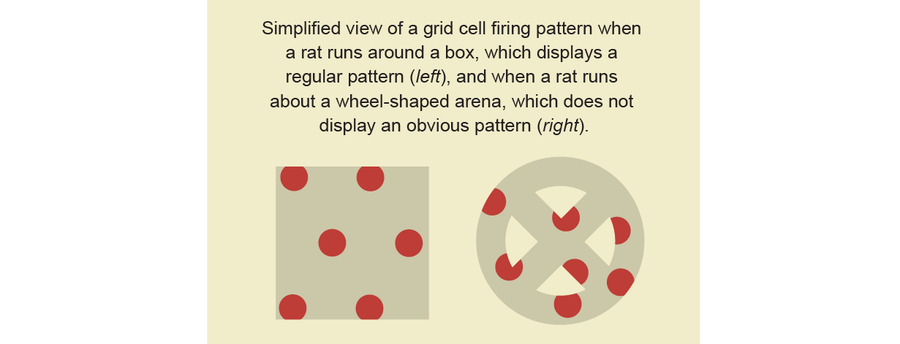
圖片來源:Jen Christiansen
在 2022 年 2 月的 Nature 論文中,包括鄧恩在內的一個數學家和神經科學家團隊使用網格細胞來測試一種稱為連續吸引子網路的理論,該理論預測某些神經元以特定模式連線在一起——即使動物處於不同情況下,該模式也不會改變。 為了測試連續吸引子網路理論,研究人員需要確定網格細胞是否總是形成環面,無論大鼠發現自己處於何種環境中。 他們在雜亂的神經學資料中搜索環面——這是 TDA 的完美工作。
這一次,研究人員沒有標記單個網格細胞放電的盒子中的位置,而是研究了整個網格細胞網路的集體活動。 他們定期使用一串 0 和 1 記錄網路的狀態,這表示每個網格細胞是否處於活動狀態。 從數學家的角度來看,這個長字串是高維空間中的一個點。 實際上,當研究人員記錄系統在不同時刻的狀態時,他們正在積累高維資料點。 這些點描述了網格細胞啟用模式隨時間演變的方式,但資料太複雜,無法用肉眼研究。
在使用一些標準技術簡化資料後,該團隊透過在不同尺度上連線資料點並檢查由此產生的單純復形,計算了系統的持久同調。 和以前一樣,當大鼠在盒子周圍跑動時,資料形成了一個環面。 但真正的考驗是研究人員從在輪狀競技場周圍跑動的大鼠那裡獲得資料時。 令他們高興的是,它再次形成了一個環面。
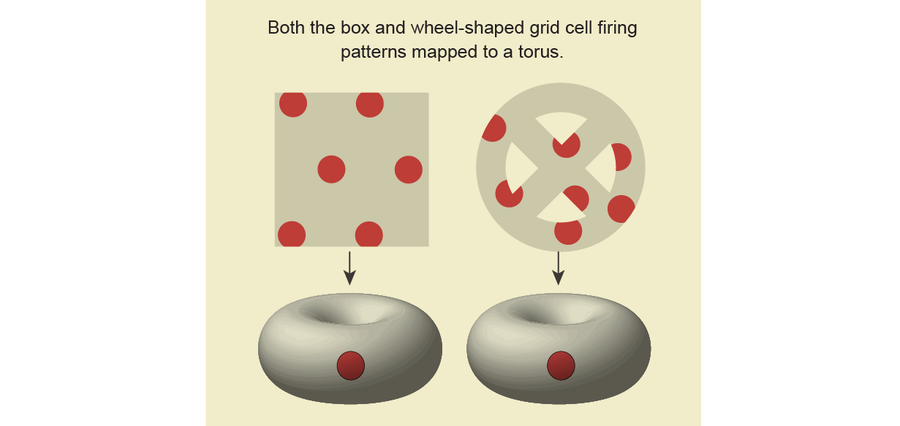
圖片來源:Jen Christiansen
研究人員甚至能夠從一隻正在睡覺——可能正在做夢——的大鼠那裡收集資料。 同樣,他們發現了一個環面,無論大鼠的環境或存在狀態如何,形狀都持續存在,這一發現支援了連續吸引子網路理論。 甜甜圈形狀似乎是網格細胞如何表示空間的內在特性。
拓撲資料分析的許多這些應用只有在強大的新型計算工具的支援下才有可能實現。“如果人們沒有認真開始構建演算法,這一切都不會發生,”牛津大學的數學家維迪特·南達說。“如果它不有效,如果它不能很好地擴充套件,那麼無論理論多麼美妙,都沒有人想使用它。”
由於這些技術,拓撲學的用途正在蓬勃發展,直到最近,拓撲學似乎還只是一個抽象的、如果說有趣的話,數學分支。“應用越來越強大,”斯坦福大學數學家、TDA 的先驅之一貢納爾·卡爾森說。“我們真的跨越了鴻溝。”

