2021 年,一對非傳統的合作者開始了一項大膽的實驗。數學家兼數理物理學家史蒂文·雷恩和自由作曲家、鋼琴家兼長號演奏家傑夫·普雷斯拉夫花了兩年時間準備回答一個大問題:他們能否將一篇數理物理研究論文直接翻譯成音樂?更重要的是,他們的音樂創作會好聽嗎?
9 月,雷恩和普雷斯拉夫釋出了他們的心血結晶,“數學 + 爵士:來自量子未來的聲音。” 在薩斯喀徹溫大學的研究員雷恩和居住在加拿大溫尼伯的普雷斯拉夫首次透過電子郵件聯絡整整兩年後的同一天,他們聚集了一個由 15 名音樂家組成的“雙曲樂隊”,在薩斯喀徹溫大學表演了五部分的音樂會。每個部分都對應於雷恩的研究文章的一部分。
這場音樂會既是音樂表演,又是講座,觀眾“座無虛席”,雷恩說。講座部分剖析了論文的科學概念,並闡述了這些想法是如何轉化為音樂的。一些插圖是字面意義上的:幻燈片展示了艾略特·基恩澤創作的雙曲藝術。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
舉辦這場音樂會絕非易事。雷恩指出,由於許多音樂家都不是本地人,樂隊直到音樂會前一天晚上才在一起親自排練音樂。
雙曲能帶理論
音樂基於雷恩 2021 年發表在《科學進展》(Science Advances) 上的文章《雙曲能帶理論》,這篇文章是他與阿爾伯塔大學的約瑟夫·馬切伊科合著的。他們的目標是探索能帶理論——研究人員用它來考慮材料的能級及其構成原子——是否可以被重新構建,以解釋具有不規則、扭曲排列的雙曲材料。
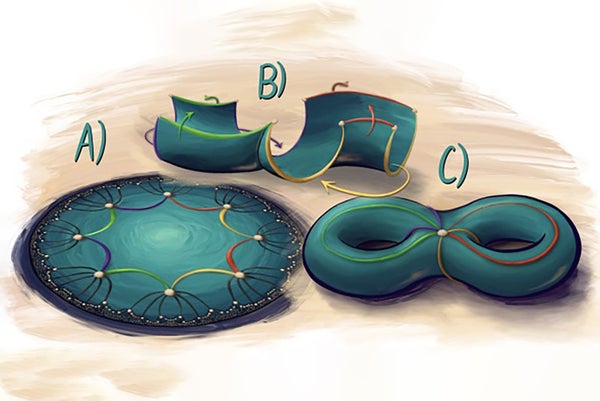
在能帶理論中,材料的能級被認為包含在懸浮在它們所屬材料上方的片狀能帶中。這些陰影能帶代表了材料的量子特性,並且這些能帶之間的相互作用對材料的行為有影響。
雷恩和馬切伊科成功地發現了一種能帶理論,該理論適用於怪異的雙曲幾何世界,這是一個打破歐幾里得“平行公設”的奇怪幾何領域。這條規則也稱為歐幾里得第五公設,它告訴我們以下內容:假設給定一條直線。對於任何不在該直線上的點,將只有一條直線既穿過該點又平行於原始直線。在雙曲世界中,至少有兩條直線將穿過該點,同時平行於給定的直線。
雷恩說,這項研究“是一種全新的材料設計方法——尤其是量子材料——透過從內到外重新設計它們的幾何形狀”。該方法涉及改變材料的能帶結構,以在材料的性質中產生期望的變化。“它們可以呈現出不尋常的、奇異的幾何形狀,”他說。
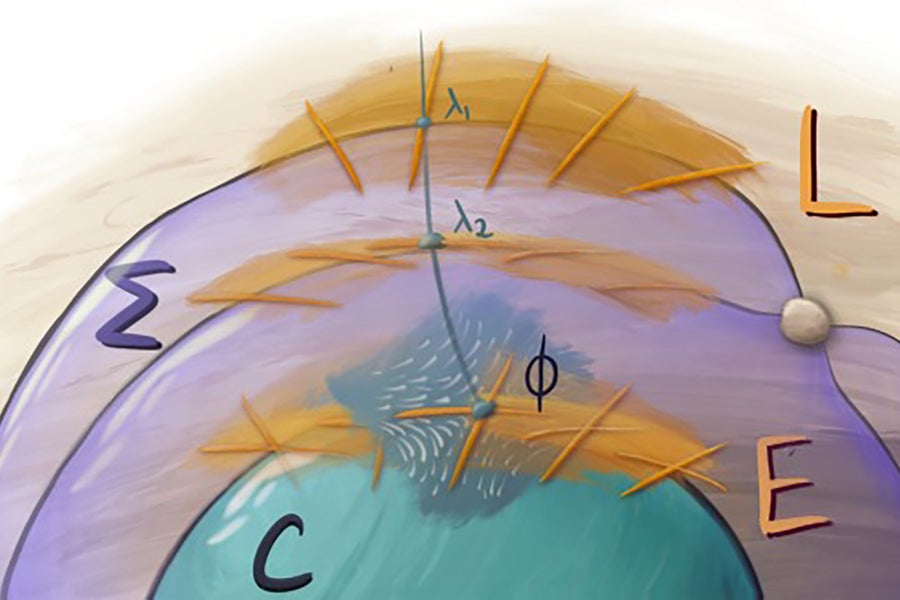
例如,這可能看起來像用八邊形平鋪彎曲表面,以便在非重疊的形狀之間沒有任何間隙。雷恩指出,在人類看來,這些八邊形的邊緣看起來是彎曲的,並且形狀看起來大小不同。但是,“如果你有一種不同的眼睛,以雙曲的方式看待世界——也許像昆蟲的複眼——[八邊形] 對你來說可能看起來都一樣,”他說。
這項工作受到了其他研究人員的廣泛關注。“我對這篇論文的作者發現的材料科學和代數幾何之間的聯絡印象非常深刻,”多倫多大學的數學家邁克爾·格羅切尼格說,他沒有參與這篇文章。
雷恩很高興將他的發現應用於研究具有“顛覆性應用”潛力的不尋常材料,例如在量子計算中。“看到有人展示了這些方法在如此具體性質的重要應用,真是令人高興,”格羅切尼格說。該論文“邀請我們純粹的數學愛好者稍微離開我們的舒適區,去探索迄今為止未知的領域,”他補充道。
轉化為音樂
創作一場數學音樂會本身就是對這項研究的一種顛覆性應用。“我不希望[音樂]是印象派的,”普雷斯拉夫說。“我希望它真正忠實於數學……我見過太多跨學科專案,它們給我的印象只是膚淺的。科學方面可能很嚴謹,而藝術方面則非常不嚴謹。”
雷恩同意這一目標。“我承諾不僅要創作一些鬆散地受到數學和科學啟發的音樂,而且還要以音樂形式逐字逐句、逐個公式地複述數學,”他說。
但是,接受這一挑戰也要求兩位專家離開他們的舒適區,並相互學習對方專業領域的概念。普雷斯拉夫沉浸線上性代數和拓撲學的專題中,這有助於闡明研究論文的內部運作原理。雷恩則投入到“儘可能多地理解[普雷斯拉夫]提出的高階音樂理念”中。
在普雷斯拉夫甚至開始創作音樂之前,兩人交流想法大約 18 個月。“令人驚訝的是,直到 9 月 20 日演出前一天,我才在現實生活中見到傑夫,”雷恩說。“這一切都是透過 Zoom 進行的,因為疫情和距離的原因。這是一種令人著迷的工作方式——我們甚至可以透過純粹的虛擬方式完成這項工作。”
雙重賦格曲和無限形狀
很難準確指出雷恩和普雷斯拉夫是否實現了他們的宏偉目標:將雷恩論文中的主要思想直接轉化為爵士音樂。與數學研究不同,沒有“證明”表明他們實現了目標。不過,兩人對他們的成果感到滿意。“在演出前甚至六個星期,完成這件事都從來不是一件確定的事情,”雷恩說。
雙曲樂隊的演奏者沙阿·薩迪科夫是一位居住在巴爾的摩的中提琴家,他說音樂會的一個亮點是普雷斯拉夫使用了一種“非常難以實現”的雙重賦格曲,來表示構建“無限形狀”的過程,薩迪科夫說。從數學上講,這意味著建立一個“沒有開始,沒有結束”的物體,薩迪科夫說。從音樂上講,創作雙重賦格曲包括使“一個想法成為音樂作品的基礎,然後你採用完全相同的想法[並且]你將它稍後放在它的頂部”,等等,他說。“你創造了這些想法的層次。然後你可以使用與此相反的想法,要麼採用相同的音樂想法[並且]將其向後或向上放置,”他指出。
對於雷恩來說,一個亮點是聽到普雷斯拉夫對“所謂的粒子-波二象性或雙曲能帶理論中的位置-動量二象性”的音樂演繹。在這種情況下,動量可以比位置佔據更多的維度。“我們想在音樂中捕捉到從比如說二維到四維的跳躍,在最簡單的這些材料中,這些材料是基於八邊形雙曲晶格的,”雷恩說。
“聽到[普雷斯拉夫]嘗試在音樂中引入額外的聲音,以捕捉額外的自由度,突然跳躍到額外的兩個維度,對我來說是一次感人的經歷,”雷恩說。“我喜歡看著觀眾在[他]解釋之後試圖聽到那些額外的聲音。”
音樂會還包括另一項藝術元素:基恩澤的手繪插圖。基恩澤現在是加州大學伯克利分校的研究生,他為一個相關的研究專案創作了數學藝術作品,這是他和雷恩在他在馬里蘭大學帕克分校讀本科時一起完成的。“這是一種嘗試透過視覺鏡頭講述故事的方式,”雷恩說。在音樂會中,這些插圖幫助增強了對數學和科學的音樂和口頭解釋。
雷恩認為,透過音樂和藝術的視角重新詮釋這項工作,是一種使其走向圓滿的方式。他的論文中使用的許多數學和科學概念都借鑑了藝術世界的思想。例如,“雙曲平鋪非常讓人聯想到”荷蘭圖形藝術家 M. C. 埃舍爾的標誌性木刻,他指出。雷恩計劃繼續探索融合數學和藝術視角的新方法,以便在為藝術“回饋”的同時,也為他的研究萌生新的見解。