我高中時並沒有覺得數學特別令人興奮。 老實說,我上大學後才開始學習數學,因為最初它對我來說似乎很容易。 但在我本科生涯的第一堂數學課上,我意識到我對數學的一切認知都是錯誤的。 數學一點也不容易。 我很快發現,數學可以非常令人興奮,尤其是當你超越純算術領域時。
在物理學中,真正令人驚訝的內容——那些與你對宇宙的直覺相悖的概念——大約在高中時出現,那時學生們可以瞥見奇異的量子世界,並接觸到愛因斯坦的廣義和狹義相對論。 學校數學無法跟上這些奇蹟。 你學習基本的算術運算、積分和求導、機率和向量的基本處理。 如果你幸運的話,有抱負的老師可能會向你展示一個簡單的證明。 就這樣。 因此,難怪許多學生未能對這門學科培養真正的熱情。
然而,數學提供了各種各樣的驚喜,例如巴拿赫-塔斯基悖論,它指出你可以幾乎神奇地將一個球體翻倍,或者存在無限多個不同的無窮大。 真正讓我震驚的是發現數學與最奇異的物理現象是如此深刻地交織在一起。 並非一定是量子物理本身產生了令人難以置信的效果; 不,系統始終遵循嚴格的數學規則。 正如化學家彼得·阿特金斯在他 2003 年出版的《伽利略的手指》一書中所說,“確定數學在哪裡結束,科學在哪裡開始,就像描繪早晨薄霧的邊緣一樣困難且毫無意義。”
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您將有助於確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
物理學家邁克爾·貝里的一項發現比任何例子都更好地說明了數學和物理學的融合。 1984 年,貝里揭示了量子力學深刻且在很大程度上出乎意料的幾何方面。 貝里意識到,這種幾何賦予了量子粒子一種記憶。
實際上不應該發生任何事情
當時,貝里正在研究一個非常簡單的系統:處於變化環境中的粒子(例如中子)的量子態。 中子具有一種稱為自旋的量子特性,它就像粒子隨身攜帶的微小磁鐵。 這種自旋可以向上或向下定向——因此物理學家說中子具有“自旋向上”或“自旋向下”。 中子的自旋受外部磁場的影響。
貝里使用數學方法來研究如果磁場方向緩慢變化,中子會發生什麼。 根據 20 世紀初提出的所謂絕熱定理,粒子的量子性質不應因此而改變:其能量、動量、質量和自旋保持不變。
如果你緩慢地轉動磁場的方向,然後再將其移回原始方向,原則上,這種動作實際上不應該改變任何東西。 “至少,多年來,這在物理學家中是一種普遍的觀點,”貝里在 1988 年 12 月的《大眾科學》雜誌上的一篇文章中寫道。 但“波函式相位的變化被忽略了。”
量子力學最奇怪的現象之一是波粒二象性:量子物體可以被想象成點狀形狀,但它們也表現出像水一樣的波動行為。 相位描述了波相對於某個角度的位移——例如,餘弦函式只不過是相位移動的正弦函式。
正如貝里在他的計算中認識到的那樣,磁場的緩慢變化會導致中子的波函式旋轉一定的相位。 這意味著粒子的波函式顯示了過去發生的事情(在本例中為磁場的變化)。 此外,貝里認識到,這種相位不僅發生在粒子在磁場中的特殊情況下。 量子系統緩慢改變然後返回到其原始條件的各種情況都會在波函式中留下痕跡。
貝里的開創性工作發表後不久進行的實驗證實了這些想法。 如果你熟悉量子力學,那麼你可能知道波函式不是一個可以直接觀察到的量。 然而,有一種方法可以透過使用第二個粒子作為參考來測量相移。 在這些實驗中,物理學家允許兩個粒子(例如中子)碰撞,其中一個粒子之前處於可變磁場中。 當中子相遇時,它們的波函式相互作用。
這些函式的行為類似於水波:如果波谷和波峰對齊,它們會相互加強; 另一方面,如果它們彼此錯開,它們會減弱或完全消失。 這些現象分別稱為相長干涉或相消干涉。
實驗表明貝里是正確的:中子是異相的,發生相消干涉。 這一觀察結果表明,其中一個粒子曾經短暫地處於變化的磁場中。 即使其任何可測量的性質都沒有因此而直接改變,但其改變的波函式暴露了這一點。
彎曲的宇宙
但是貝里是如何知道粒子會經歷相移的呢? 事實上,只要存在曲率,就會出現這種相位。 這就是為什麼相位在愛因斯坦的廣義相對論中起著重要作用——他用該理論來描述引力。
一些專家認為,廣義相對論更多的是幾何學而不是物理學。 根據該理論,物質彎曲時空,而這種變形導致質量相互吸引——我們將其感知為引力現象。 我喜歡把它想象成一張橡皮片,上面放置著重物,使橡皮片變形,從而影響物體。 然而,這種視覺化存在一些缺陷:時空在這個概念中是二維的,我從我的三維世界俯視它。 另一方面,廣義相對論描述了四維時空的曲率,而無需從五維視角來看待它。
這就提出了一個問題,如果你不能從外部觀察物體,你如何推斷出物體的曲率? 貝里觀察到的相位在這裡有所幫助。
假設我想用一種複雜的方式證明地球是球體。 為了做到這一點,我可以從我在德國某地的位置筆直向北走,越過山脈、山谷、河流、湖泊和海洋。 在這個思想實驗中,沒有什麼可以阻止我沿著直線路徑前進。 當我到達北極時,我像螃蟹一樣橫著走,向右移動,而無需轉身。 我一直走到與我開始時相同的緯度。 然後我沿著緯度向左走——同樣無需轉身——直到我回到起點。 雖然我降落在原來的位置,但我不再像開始時那樣面向北方,而是面向東方。 因此,這次往返旅行並沒有改變我這個人(除了可能身體上的勞累),但我已經轉動了一定的角度。
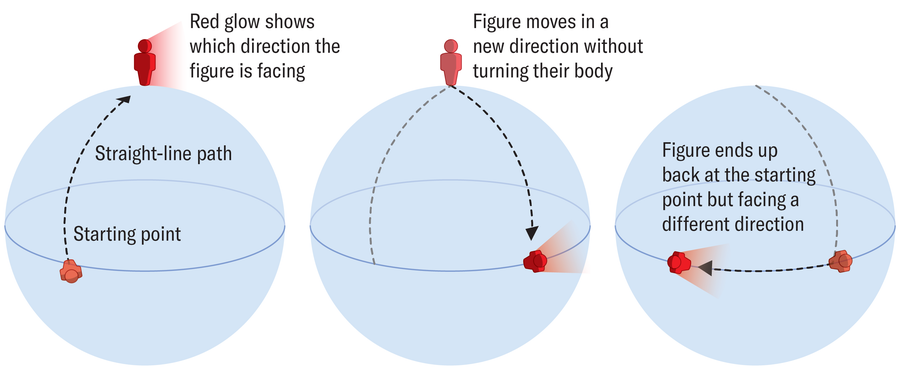
阿曼達·蒙塔內斯
如果我沿著平坦的平面走相同的路徑,我會在沒有任何旋轉的情況下返回起點。 但在這個設定在我們彎曲的星球上的思想實驗中,發生在我身上的事情與貝里理論中的波函式相同:它接收到一個相位,一個使其移動的角度。
我在旅途中獲得的這個角度完全取決於地球的幾何形狀。 其值與我的路徑所包圍的面積成正比。 因為沒有其他因素影響相位——既不是我的速度,也不是我是否休息——所以它被稱為“幾何相位”。
對於數學家來說,這在貝里發表他的著作時並不是什麼新鮮事。 他們幾十年前就知道了這個概念。 但沒有人將幾何相位應用於量子力學過程。 波函式中的相位揭示了所謂的引數空間的幾何形狀。 這是一個抽象的、高維的空間,它結合了所有可能影響波函式的引數(例如磁場、能量、位置和速度)。 磁場方向(或其他引數)的短期變化描述了這個空間中的一條閉合曲線——就像我在地球上的圓形路徑一樣。 因為這個引數空間通常是彎曲的,這會在波函式中留下痕跡。
“因此,幾何相位可以被視為系統對‘系統在引數空間中採取了什麼路徑?’這個問題的最佳答案,”貝里在他的 1988 年《大眾科學》文章中寫道。“從這個意義上說,它是一種量子‘記憶’。”
因此,貝里揭示了量子系統和幾何學之間深刻的聯絡,事實證明這是非常有價值的。 以他的名字命名的貝里相位可以用來解釋量子霍爾效應等現象,這種效應發生在某些固體中,並在貝里發現之前提出了許多問題。
所有這一切都非常令人興奮。 然而,對我來說,最令人印象深刻的是,貝里透過借鑑現有的數學概念,開創了幾何量子物理學這一新的研究領域。 他不必在物理學或數學中新增任何新東西——相反,數學使揭示物理學中完全出乎意料的東西成為可能。
本文最初發表於《Spektrum der Wissenschaft》,經許可轉載。
