信任但要核實。這種表達捕捉了依賴他人和仍然希望保持對局勢一定程度控制之間的緊張關係。數學家阿迪·沙米爾在開發現在被稱為“沙米爾秘密共享”的演算法時,一定考慮過這個挑戰,該演算法以他的名字命名。
為了理解它,以下謎題可以提供幫助:假設一位老婦人想將她的保險箱(用密碼鎖保護)的內容遺贈給她的五個兒子,但她對他們每個人都持懷疑態度。她擔心如果她只向其中一個兒子透露密碼,他就會帶著裡面的東西逃之夭夭。因此,她想給每個兒子一個線索,只有五個兒子一起工作才能開啟保險箱。這位婦人應該怎麼做?
這項任務可能看起來很簡單。例如,如果密碼鎖需要一個五位數的密碼,她可以給每個兒子一個數字,以便他們可以一起開啟它。但在這種情況下,如果三個兒子聯手,他們很可能會繞過其他兩個兄弟。三個盟友只差兩個數字才能得到完整的密碼,因此他們可以快速嘗試可能的數字組合以獲得夢寐以求的內容。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和想法的具有影響力的故事的未來。
因此,這位婦人正在尋找一種分發資訊的方式,這種資訊只有在所有五個兒子一起工作時才能使用。如果五個兒子中的兩個、三個或四個聚在一起,組合後的資訊內容必須是無用的。而這個要求使任務變得更加複雜。
但在 1979 年,這個挑戰並沒有讓沙米爾氣餒。兩年前,他與羅恩·李維斯特和倫納德·阿德曼一起開發了所謂的“RSA 演算法”。這是第一個被廣泛採用的非對稱加密演算法,至今仍在使用。
沙米爾秘密共享的實際應用
為了理解沙米爾秘密共享方法,檢視一個具體的數字示例會有所幫助。假設這位婦人的秘密程式碼是 43953,並且為了簡單起見,我們假設她只有兩個兒子。(我們稍後將逐步解決有五個兒子的情景。)
如果這位婦人委託一個兒子“439”,另一個兒子“953”,她就給了他們兩人相同數量的資訊。現在,如上所述,兒子們可以各自嘗試猜測缺少的兩位數字。他們每個人最多隻需要嘗試 100 個組合即可開啟保險箱。
因此,沙米爾需要不同的解決方案。最好是每個兒子收到的資訊乍一看與解決方案無關。但是,如果將兩條資訊放在一起,您應該能夠推斷出數字組合 43953。並且有一種優雅而簡單的方法可以藉助線性方程來做到這一點。
每條直線都由兩個點唯一確定。沙米爾意識到秘密數字可以編碼在一條直線上:例如,作為它與 y 軸相交的高度。如果您給兩個兒子每個人在直線上一個點的座標,他們只能一起確定數字 43953。一個兒子單獨一個點什麼也做不了:有無數條直線穿過一個點。
例如,這位婦人可以選擇直線方程 y = 5x + 43953,並給大兒子一個點 P1 (33503, 211468) 的座標,給另一個兒子第二個點 P2 (85395, 470928) 的座標。即使這兩個兒子的數學不好,他們也可以簡單地在平面上標記這兩個點,用尺子連線它們,然後讀出直線與 y 軸的交點,即可得到保險箱的解決方案。
因此,兩個兒子的問題就解決了。如果這位婦人有三個兒子,她可以以類似的方式進行。然而,在這種情況下,她不會選擇直線,而是選擇拋物線來隱藏程式碼。
例如,這位婦人可以選擇二次函式 y = 5x2 + 10x + 43953,並給她的每個兒子一個拋物線上的點。同樣,與 y 軸的交點對應於所需的解決方案:43953。兩個兒子不能合謀反對第三個兒子,因為無數條拋物線可以穿過兩個點;兩個兒子需要他們兄弟的幫助才能找到與 y 軸的交點,從而找到保險箱的密碼。
該原理可以推廣到任意數量的參與者:有四個兒子的婦人可以解方程 y = ax3 + bx2 + cx + 43953。(因為 3 是此方程中的最高指數,所以它被稱為三次多項式方程。)有五個兒子的婦人使用四次多項式方程(例如 y = ax4 + bx3 + cx2 + dx + 43953),依此類推。該原理基於所謂的“多項式插值”:一般來說,需要 n + 1 個點才能唯一確定 n 次多項式。
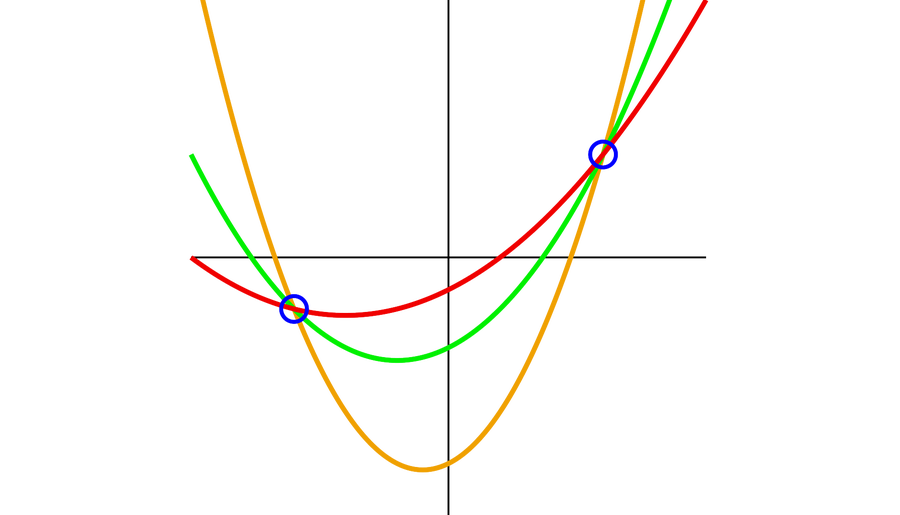
有無數條拋物線穿過兩個點。 來源:Vlsergey/Wikimedia (CC BY-SA 3.0)
這位婦人還可以讓她的兒子們成對訪問保險箱。在這種情況下,她依靠兒子們互相控制,因此需要五個人中的兩個人同時在場才能開啟保險箱。為此,這位婦人可以再次選擇一條直線作為基礎,並在其上標記五個隨機選擇的點。透過給每個兒子一個點,她確保他們中的兩個人可以確定密碼——無論哪兩個兒子相遇。
但這裡有一個問題。讓我們回到有五個兒子的情景。如果他們中的四個合謀反對一個兄弟,他們可以使用這四個點儘可能地解出四次方程。當然,他們無法直接從中讀取密碼。最後,他們留下了一個帶有兩個未知數的方程:引數 a 和密碼 c(在我們的示例中是 43953,但兒子們不知道)。
然而,這四個兒子知道 c 必須是整數。例如,如果這位婦人總是給他們曲線上點的整數座標,那麼他們可以假設 a 可能也具有整數值。這大大限制了可能性的範圍。兄弟們可以使用計算機程式嘗試不同的解決方案——然後可能會確定正確的密碼。
進入不同的數字範圍
為了避免這種情況,沙米爾還有另一個訣竅:他沒有使用通常的實數進行計算,而是將自己限制在一個更小的數字空間:有限域。在這個數字系統中,四種基本算術運算(加法、乘法、減法和除法)可以像往常一樣應用。然而,這個數字空間不是包含無限數量的數字,而是隻包含有限數量的數字。

如果您想確定 n 次多項式,您至少需要 n+1 個點。 來源:MartinThoma/Wikimedia (CC BY-SA 3.0)
雖然這聽起來可能很陌生,但我們每天都在使用有限域——例如,每當我們看時鐘時。如果您只看小時,數字範圍包括 12 或 24 個數字。但我們仍然在這個有限的空間中計算:如果現在是晚上 11 點,有人說麵包店七小時後開門,那麼很明顯他們指的是六點鐘。
在沙米爾秘密共享中,也選擇了一個受限的數字範圍,但上限通常是一個大的質數。如果以這種方式選擇數字空間,則多項式的圖形不再對應於連續曲線,而是對應於平面中隨機分佈的點。
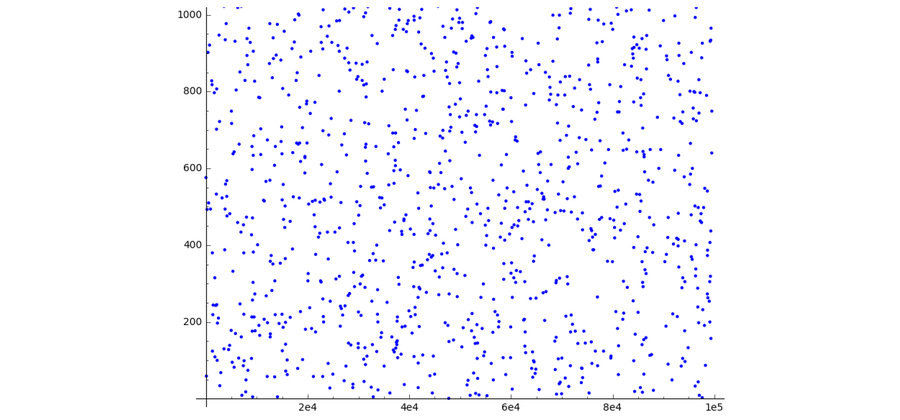
當您在有限域中定義多項式方程時,平滑曲線會變成一組點。 來源:Wolfmankurd/Wikimedia (CC BY-SA 4.0)
透過將這位婦人的計算限制在這樣的數字範圍內,兄弟們實際上不可能合謀反對彼此。為了找出正確的數字程式碼,他們必須一起工作。
本文最初發表於Spektrum der Wissenschaft,並經許可轉載。
