古代學者希帕索斯因發現無理數而被處死——或者至少傳說如此。公元前五世紀究竟發生了什麼,目前尚不清楚。
希帕索斯是畢達哥拉斯學派的成員,這是一個涉及數學和數字神秘主義的教派,以及其他事物。畢達哥拉斯學派教義的核心要素與和諧的數字關係有關,其中包括整數的分數。
他們認為,整個世界都可以用有理數來描述,包括自然數和分數。然而,故事是這樣的,當希帕索斯檢查畢達哥拉斯學派的象徵——五角星的長度比率時,他意識到該形狀的某些邊的長度無法表示為分數。因此,他提供了無理數存在的第一個證明。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和想法的具有影響力的故事的未來。
從這裡開始,關於希帕索斯的說法開始分歧。有些人說畢達哥拉斯學派對這種斷言感到不滿,因為這樣的數字與他們的世界觀背道而馳。在其他故事中,希帕索斯公開了他的成果,因此違反了該教派的保密性。無論如何,他在發現後溺水身亡。一些報道聲稱畢達哥拉斯學派將他從船上扔下去。其他人則斷言他的死是一場意外,畢達哥拉斯學派認為這是神聖的懲罰。
目前對現有歷史證據的解讀表明,這些故事純屬傳說。希帕索斯的發現——假設他真的做出了這個發現——很可能被譽為一項數學成就,令畢達哥拉斯學派感到自豪。事實上,圍繞畢達哥拉斯學派的許多可疑故事都是因為他們因其哲學和政治思想而受到迫害。
可用的事實有限。這個社團很可能由薩摩斯的畢達哥拉斯在現在的義大利南部創立——這位希臘學者以著名的勾股定理命名(儘管他是否證明了這個定理也不清楚)。除了對數學的興趣外,畢達哥拉斯學派還有許多觀點使他們與古希臘其他人區分開來。他們拒絕財富,過著素食主義的苦行生活,並相信輪迴。最終,該團體遭受了幾次襲擊,在畢達哥拉斯去世後,該社團完全消失了。
關於希帕索斯的故事,歷史學家一致認為最有可能真實的要素是,畢達哥拉斯學派在某個時候證明了某些量是不可公度的,由此推匯出無理數的存在。
分數之外的數字
我們現在在學校裡瞭解到,有些值——所謂的無理數——無法表示為兩個整數的比率。但這種認識遠非顯而易見。畢竟,無理數值至少可以用分數來近似——儘管有時這很困難。
希帕索斯——或另一位畢達哥拉斯學派成員——提出的著名的無理數證明最容易用等腰直角三角形來說明:考慮一個兩條邊長均為a的三角形,這兩條邊形成一個直角,與長度為c的斜邊相對。
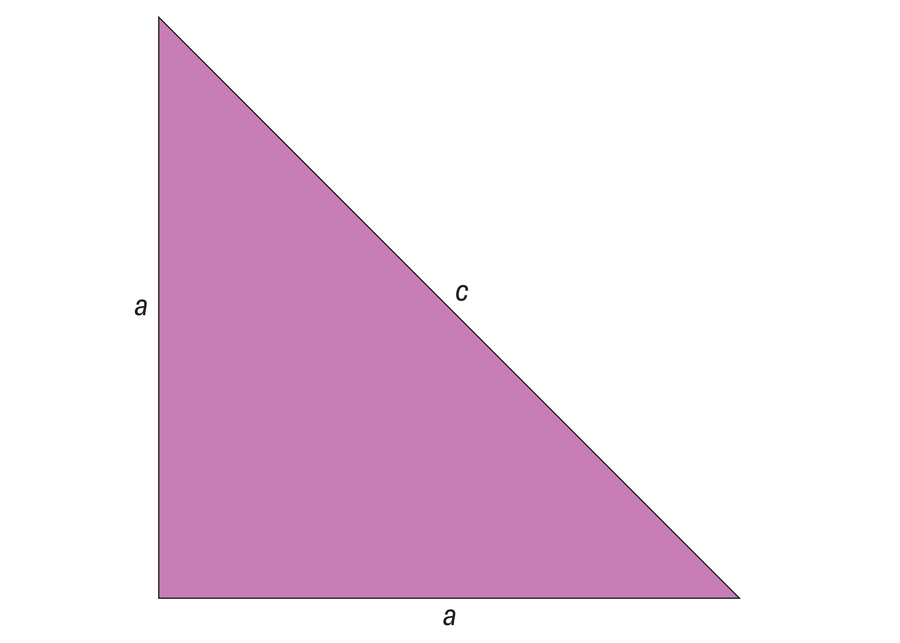
無理數的存在最好用等腰直角三角形來解釋——也就是說,一個兩條邊長度相等並形成直角的三角形。
Manon Bischoff/Spektrum der Wissenschaft
這樣的三角形具有固定的縱橫比a⁄c。如果a和c都是有理數,則可以選擇三角形的邊長,使a和c各自對應於可能的最小自然數(即它們沒有公約數)。例如,如果縱橫比為2/3,您將選擇a = 2 和 c = 3。假設三角形的長度對應於有理數,則a和c是整數並且沒有公約數——或者至少每個人都這麼認為。
反證法
希帕索斯使用這種思路來建立一個矛盾,這反過來證明了最初的假設一定是錯誤的。首先,他使用勾股定理(古老的a2 + b2 = c2)將斜邊c的長度表示為兩條等邊a的函式。或者,用數學方式表達:2a2 = c2。由於a和c是整數,因此從前面的方程可以得出c2必須是偶數。因此,c也可以被2整除:c = 2n,其中n是自然數。
將c = 2n代入原始方程得到:2a2 = (2n)2 = 4n2。2可以在兩邊約簡,得到以下結果:a2 = 2n2。由於a也是一個整數,因此得出a是平方數,因此也是一個偶數。然而,這個結論與最初的假設相矛盾,因為如果a和c都是偶數,則它們都不能是除數。
這個矛盾使希帕索斯得出結論,等腰直角三角形的縱橫比a⁄c不能對應於有理數。換句話說,存在一些數字無法表示為兩個整數值的比率。例如,如果形成直角的邊a = 1,則斜邊c = √2。正如我們今天所知,√2是一個無理數,其小數位無限期地延續下去,永不重複。
從我們目前的角度來看,無理值的存在似乎並不太令人驚訝,因為我們在很小的時候就接觸到了這個事實。但我們只能想象,大約2500年前的這種認識可能會引發什麼。它可能會顛覆數學世界觀。因此,關於它的發現有如此多的神話和傳說也就不足為奇了。
本文最初發表於《Spektrum der Wissenschaft》,經許可轉載。
