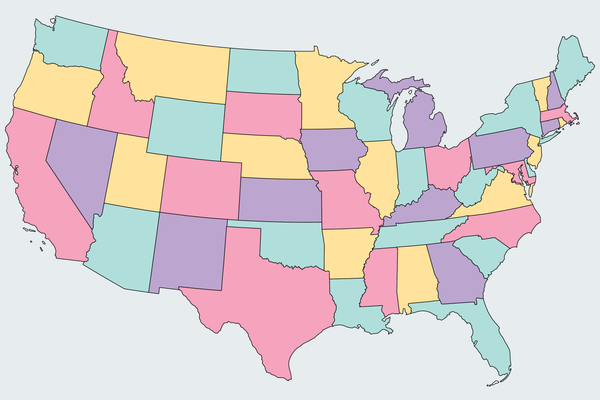
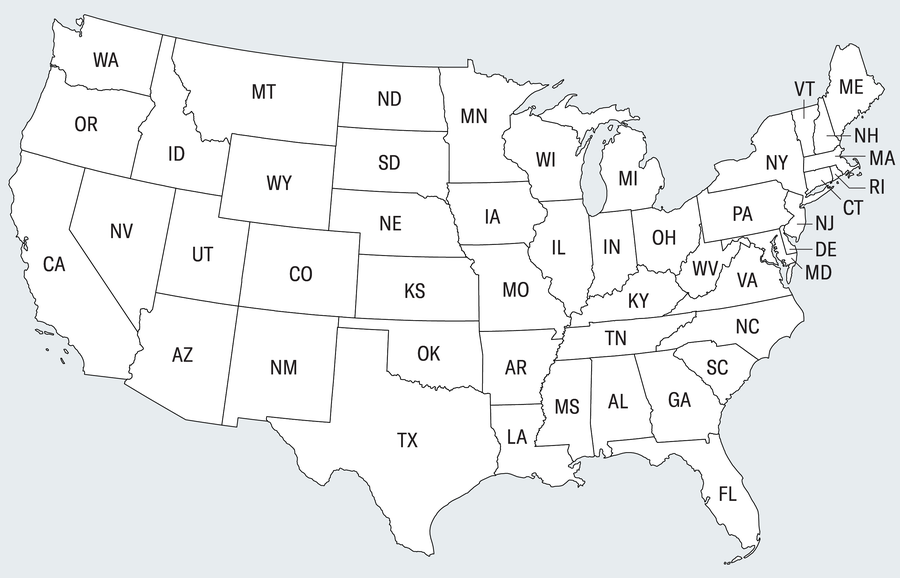
1852 年,數學家弗朗西斯·格思裡提出了一個看似簡單的問題,這個問題引發了無休止的爭論,導致大量已發表的論文被推翻,並最終以一種突破數學原則的方式得到解決。這個引起如此多麻煩的難題是:為地圖著色所需的最小顏色數是多少,才能使相鄰的州或其他指定區域不具有相同的顏色?以下是它的工作原理。看看下面美國本土的黑白地圖。它看起來有點簡陋。為了使地圖更生動並清晰地突出其邊界,製圖師傾向於為區域著色。
金俊
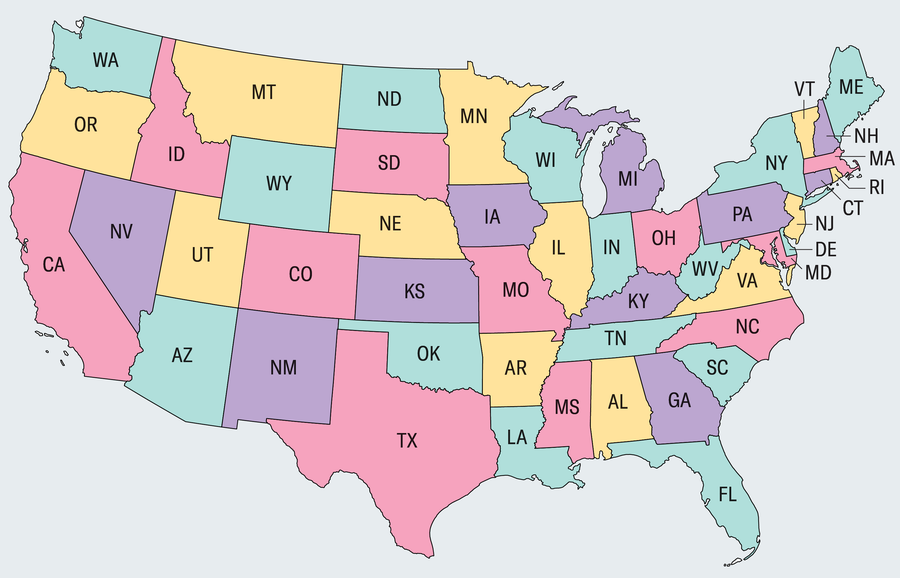
當然,我們不希望相鄰的州具有相同的顏色,因為那樣會使邊界更加混亂。在這種約束下,我們使用了四種顏色來填充黑白地圖。我們只用三種顏色可以做到嗎?其他地圖可能需要五種或六種顏色嗎?
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
金俊
這個問題中的地圖不必對應真實的地理位置——任何將平面表面劃分為不同區域的方式都符合條件。問題是,給定任何這樣的地圖,需要多少種顏色來填充每個區域,才能使沒有兩個相鄰區域具有相同的陰影。一些基本規則:每個不同的區域必須是連通的(從技術上講,密歇根州在美國地圖中違反了這一規則,因為密歇根湖將該州分割成兩個不連通的部分)。要使兩個區域被視為相鄰,它們必須共享一定長度的連續邊界;僅在一個點(或離散的點集)接觸不符合條件。例如,猶他州和新墨西哥州僅在一個角上接觸,因此在我們的目的中不被視為鄰居。
在規則確立後,這裡有一些答案令人驚訝的問題。假設我打印出一張包含數千個區域的複雜地圖的大海報。您需要多長時間才能確定該地圖是否可以用兩種顏色著色?三種顏色?四種顏色?您不一定需要找到 著色方案;只需確定每種顏色數量是否存在即可。奇怪的是,儘管對於所有數字來說,任務看起來幾乎相同,但完成每種顏色數量的任務所需的時間卻截然不同。使用最著名的方法
確定兩種顏色是否足夠大約需要一個小時。要做到這一點,選擇任何區域併為其著色,例如紅色。這會將該區域的所有鄰居強制變為您的第二種顏色,例如藍色。反過來,它們的所有鄰居都變成紅色,依此類推,在地圖上蔓延。最終,您要麼遇到鄰近區域共享顏色的衝突,在這種情況下,不存在“雙色著色”,要麼顏色在整個地圖中無衝突地傳播,在這種情況下,您就找到了有效的著色方案。根據粗略計算,對於包含 3,000 個區域的地圖,以每著色方案一秒的速度計算,需要花費 50 分鐘的時間。
假設地圖無法僅用兩種顏色填充。確定三種顏色是否足夠將需要更長的時間。下午會悄然流逝。當您瘋狂地塗寫無盡的配置,尋找可行的配置時,幾周的時間也會從日曆上剝落。為了繼續進行下去,您必須將正在進行的任務傳遞給您的孩子,然後再傳遞給他們的孩子。幾代人的生命都致力於尋找這張地圖的三色著色方案,也無法撼動這項工作量,因為太陽在數十億年後不可避免地吞噬地球,並結束這種愚蠢的努力,使我們幾乎無法接近答案。
確定任意地圖是否具有三色著色方案是困難的。這裡的“困難”是一個技術術語,表示它屬於一類以其耗時難度而聞名的計算問題,稱為 NP 完全問題。對於此類問題,我們不知道任何比或多或少地蠻力搜尋每個可能的解決方案更快的方法。隨著問題規模的增加,搜尋空間呈指數級增長。對於只有少量區域的小地圖,我們可以負擔得起窮盡搜尋每種可能的三色著色方案,直到找到可行的方案(或得出結論,認為不存在可行的方案)。但是,為包含數千個區域的地圖分配三種顏色的方式數量是如此之大,以至於窮舉搜尋變得毫無希望。
那麼四種顏色呢?嗯,這大約需要一秒鐘,或者您需要說“是”的時間,因為每張地圖都可以用四種顏色著色。這個結果就是臭名昭著且長期存在爭議的四色定理。
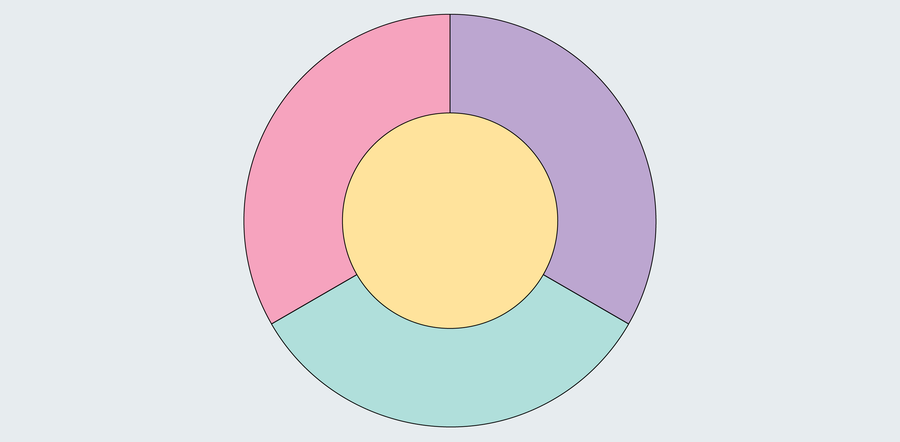
當格思裡在 1852 年首次推測四色定理時,他注意到他只需要四種顏色就可以正確地填充英格蘭的縣。他懷疑這條規則可以推廣到任何地圖,但是儘管任何幼兒園的孩子都能理解這個問題,但他和他的同事都無法證明它。很明顯,三種顏色並不總是奏效,如下面的圓形圖所示,其中每個區域都與所有其他區域相鄰。
金俊
但是沒有人能找到需要五種顏色的地圖。由於這個問題受阻,數學家奧古斯都·德·摩根對此變得痴迷,並得出結論,必須在數學基礎上新增一個新公理——在數學中,公理是指未經證明而被假定為真的陳述,更復雜的陳述可以從中推匯出來——以解決格思裡的猜想。
這種狂熱的挫敗感表面上在 1879 年結束了,當時出現了一個證明,證明四種顏色總是足夠的。一年後,第二個獨立的證明強調了這一點。隨著問題得到解決,榮譽也隨之而來,被吸引的數學家回到了他們通常的研究工作中——除了一些人。在第一個證明發表 11 年後,兩個證明都被推翻,而難以捉摸的四色定理又恢復為四色猜想。英格蘭達勒姆大學的珀西·約翰·希伍德揭露了原始證明中的漏洞,但他取得了一些進展,證明五種顏色總是足以填充任何地圖。
這使數學界處於相當尷尬的境地。一個看似如此簡單的問題只有兩個答案——四個或五個——但哪個是正確的?這種情況將持續近一個世紀。
儘管沒有人能找到需要五種顏色的地圖,但也沒有人能排除存在這種地圖的可能性。由於地圖的數量是無限的,因此永遠無法單獨檢查每張地圖。解決問題的一個關鍵步驟是將問題簡化為可以單獨檢查的有限的案例集。從無限到有限的飛躍似乎很大,但是要檢查的案例的龐大數量仍然遠遠超過了任何人可以手動處理的數量。
因此,當時的伊利諾伊大學的數學家肯尼斯·阿佩爾和沃爾夫岡·哈肯轉向了一個大膽的想法:程式設計計算機來處理它們。1976 年,經過多年的微調和超過 1,000 小時的計算機執行時間,他們的演算法完成了對每個案例的窮舉檢查,並且四色定理得以確立。這是第一個在證明中使用計算機的重大定理。
數學界燃起了慶祝和沮喪並存的火焰。阿佩爾和哈肯在安大略省滑鐵盧大學的同事威廉·塔特欣喜若狂,他們“擊敗了海怪。”其他人則鄙視計算機侵佔人類智慧的想法。這件事也給數學界帶來了一個哲學問題。人類無法驗證的證明算作證明嗎?許多人預計這項工作最終會被像之前的兩個所謂證明一樣撤回。《紐約時報》甚至拒絕在最初報道這一訊息,因為四色定理的證明“反正都是假的。”
在隨後的幾十年中,多次嘗試駁斥計算機輔助證明都失敗了。數學家們此後大大簡化了證明並驗證了計算機程式碼,但時至今日,仍未發現任何無需計算機輔助即可推匯出的定理證明。儘管四色定理已被廣泛接受為事實,但對其仍存在渴望。系統分析大量配置的計算機程式並沒有確切解釋為什麼每張地圖都可以用四種顏色填充。即使數學家現在歡迎計算機作為發現的夥伴,他們仍在尋找對這個色彩繽紛的謎題更具啟發性的證明。