“在過去,我們只能收到橙子作為禮物——而且我們為此感到高興!” 這句話你有時會聽到年長的人批評當今孩子們收到的禮物過於奢華。 但他們很少提到禮品包裝。 假設你想送五個橙子作為禮物: 你會如何安排這些水果,使它們佔用儘可能少的空間和包裝紙?
事實證明,這個看似無害的問題背後隱藏著大量的數學知識。 畢竟,花了 400 多年才證明水果商們自古以來就知道的事情: 無限球體在三維空間中的最佳堆疊是透過將它們排列成金字塔形狀來實現的。 針對這個謎題的已驗證解決方案,被稱為開普勒猜想,直到 2017 年才發表。 然而,當只考慮有限數量的物體時,情況就大不相同了。
令人驚訝的是,數學家們直到 19 世紀後期才開始研究後一種問題。 挪威幾何學家阿克塞爾·圖厄是 1892 年第一個研究有限數量的二維圓的最佳排列的人。 該領域的重要進展直到接下來的幾十年才出現,當時匈牙利數學家拉斯洛·費耶斯·托特探討了這個主題。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
平面上圓的最佳排列
為了更好地瞭解這個問題,首先考慮簡化的二維情況會有所幫助。 例如,我們可以嘗試以最節省空間的方式排列幾個相同大小的硬幣。 為此,我們用一段繩子勾勒出它們的輪廓,我們將繩子拉緊在一起,並計算繩子圍成的面積。 對於 n = 2 個硬幣,很快就能找到最佳排列方式: 我們將它們放下,使它們彼此接觸。 然後,包圍半徑為 r 的兩個硬幣的最短繩子的長度為 (4 + 2π)r。
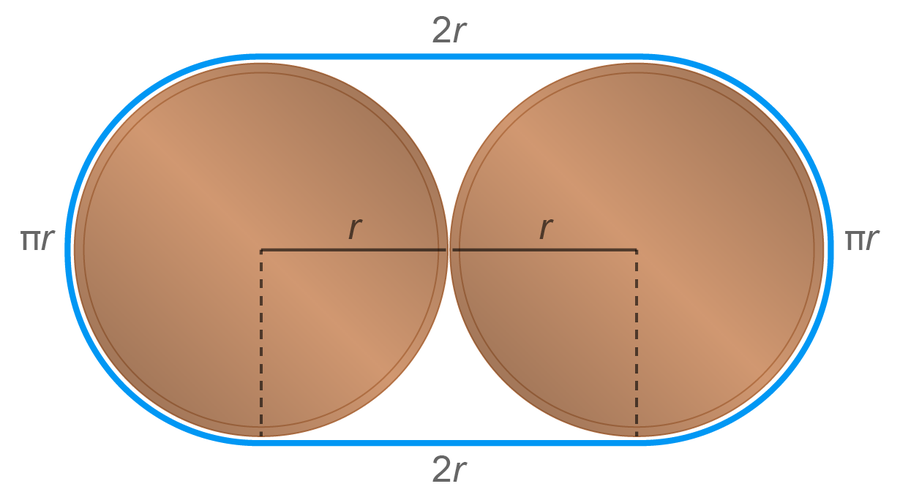
兩個最佳包裝的硬幣配對。 來源: Spektrum der Wissenschaft/馬農·比肖夫,由 大眾科學 設計風格
這個長度最好按部分計算: 加上繩子的直線部分(4 x r),再加上總共圍成一個圓的圓形區域(2πr)。 繩子圍成的總面積為 (4 + π)r2。 在這種情況下,顯然沒有更節省空間的方式來排列硬幣。
另一方面,如果手頭有三個硬幣,突然出現了兩種不同的看起來節省空間的排列方式: 一種是將它們並排排列,另一種是將它們沿著等邊三角形的角放置。 在第一種情況下,繩子會呈現香腸形狀,這就是為什麼在數學中它被稱為“香腸”包裝。 第二種情況被專家稱為“披薩”包裝。 但是哪種排列方式更節省空間: 香腸包裝還是披薩包裝?
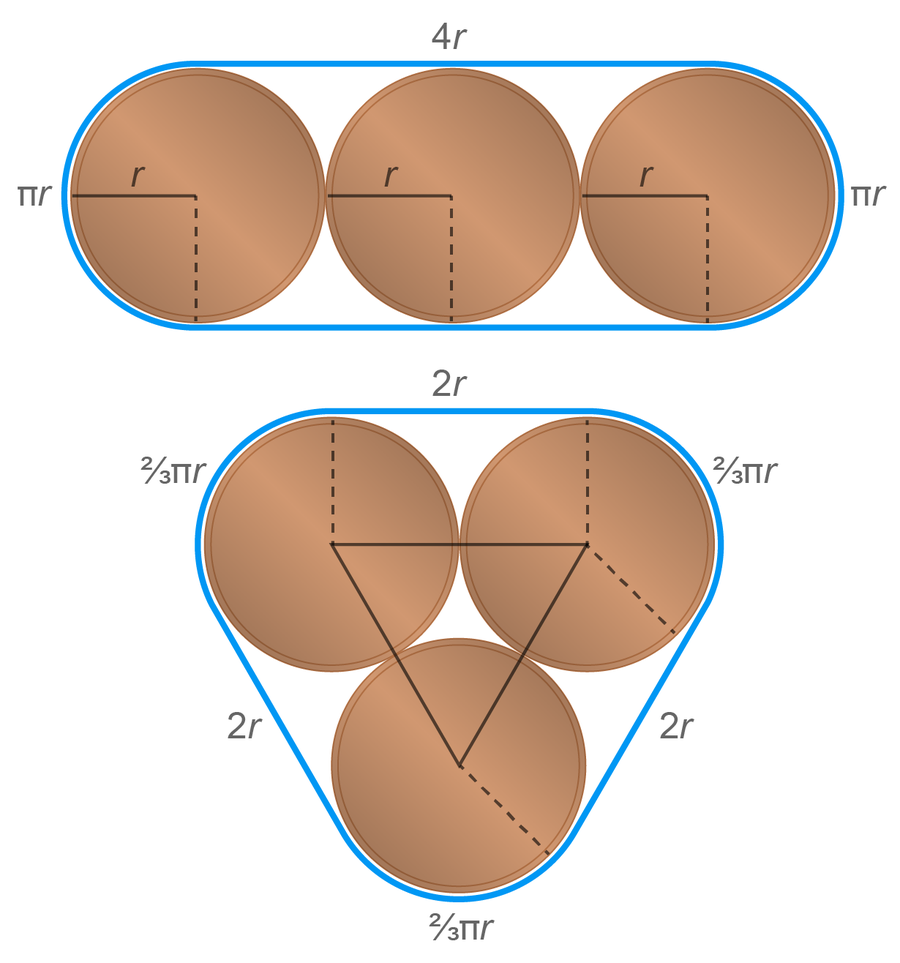
三種硬幣的兩種排列方式。 來源: Spektrum der Wissenschaft/馬農·比肖夫,由 大眾科學 設計風格
事實證明,披薩包裝更好。 這種繩子的長度為 (6 + 2π)r,,覆蓋的面積相應為 (6 + √ 3 + π)r2,而香腸包裝的繩子長 (8 + 2π)r,圍成的面積為 (8 + π)r2。 如果仔細觀察,也可以直接從圖片中看出這種差異。 香腸排列中硬幣之間的空間比披薩包裝中的空間更大。
在二維中,披薩總是勝出
事實上,可以給出繩子所需長度和限制面積的一般公式。 如果將 n 個硬幣排列成香腸形狀,則需要長度為 4(n – 1 + 2π)r 的繩子,它圍成的面積為 4(n – 1)r2 + πr2 。 另一方面,如果硬幣沿著三角形網格排列,其形狀儘可能地類似於正六邊形,則只需要長度為 2(n + π)r 的繩子,圍成的面積為 (2n + √ 3(n – 2) + π)r2。
因此,我們已經證明,對於任何數量的 n 個圓,披薩包裝都比香腸形狀更節省空間。 但它真的總是最優的嗎? 確定這一點是一項更加困難的任務。 畢竟,可能存在完全混亂的圓形排列,佔用更少的面積。 排除這種情況被證明極其困難。 這就是匈牙利數學家拉斯洛·費耶斯·托特發揮作用的地方。 1975 年,他推測,n 個圓的最佳包裝是在三角形晶格中的排列,該排列形成儘可能規則的六邊形形狀。
2011 年,數學家多米尼克·肯恩能夠證明,這個想法適用於幾乎所有 n 值。 事實上,無限平面上覆蓋無限數量的硬幣的極限情況也得到了證明。 1773 年,物理學家和數學家約瑟夫·路易斯·拉格朗日發現,沿著三角形晶格的排列是最優的——只要你只考慮有序包裝。 直到 1940 年,費耶斯·托特最終證明,這個解決方案也比任何混亂的圓形排列更節省空間。
當香腸領先時
但是球體呢? 三維情況比二維世界中最佳圓形包裝提出更多問題,這可能不足為奇。 我們至少有一個線索可以開始: 開普勒猜想指出,如果你像炮彈一樣堆疊無限多個相同的球體,它們可以最好地填充三維空間。 在第一層,你沿著三角形網格排列它們,就像二維情況下的硬幣一樣,在第二層,你在每個間隙中放置一個球體。 然後第三層再次與第一層相同,依此類推。 (換句話說,這些球體看起來像雜貨店裡橙子的金字塔形堆疊。)
但是,如果我們只考慮有限數量的球體,情況就大不相同了。 現在我們又回到了用包裝紙包裹橙子的例子。 如果你只有一個或兩個橙子,那麼如何最佳地排列它們就一目瞭然了。 如果你有三個,任務就更復雜了。 你可以將它們排成一排(香腸包裝)或像以前一樣用它們形成一個三角形(披薩包裝)。 情況類似於三個硬幣的情況,只是你處理的是球體。 為了找出在這種情況下哪種包裝最節省空間,你可以比較排列的體積。
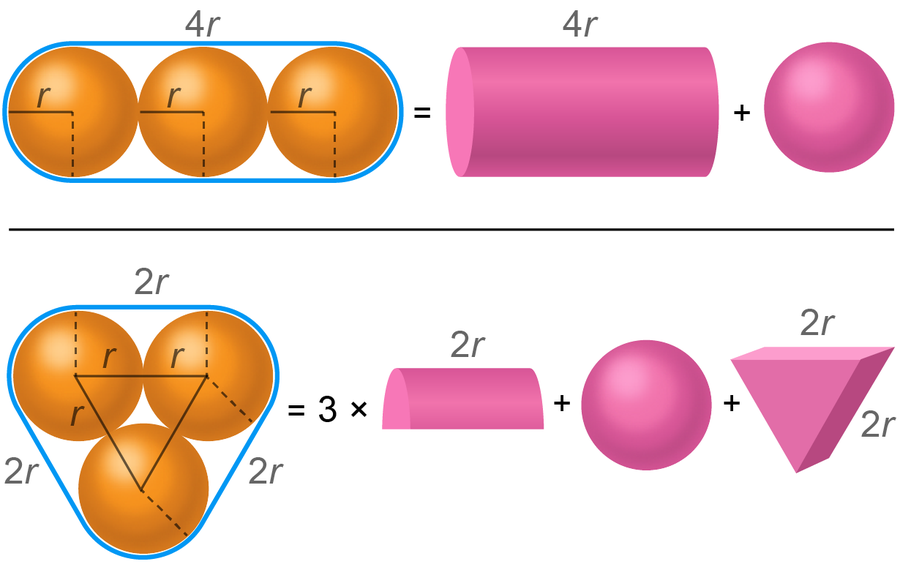
為了找到包裝三個球體的最佳方法,你必須計算每種情況下的體積。 來源: Spektrum der Wissenschaft/馬農·比肖夫,由 大眾科學 設計風格
為了開始,它有助於再次將球體的外殼分解為單個幾何形狀,並將它們的體積相加。 在香腸包裝的情況下,這非常簡單: 形狀可以分為一個圓柱體和一個球體,它們的總體積為 16⁄3π r3 ≈ 16.76r3。 披薩包裝有點複雜。 你得到三個半圓柱體、一個三角稜柱和一個球體,它們的總體積為 13⁄3πr3 + 2√ 3r3 ≈ 17.08r3。 因此,在這種情況下,香腸包裝更節省空間。 事實證明,香腸排列確實可以最佳地包裝。
香腸災難
如果你再新增一個球體,使 n = 4,你可以區分三種不同的排列方式。 同樣,你可以將球或橙子一個接一個地排成一行(香腸),或者將它們分佈在平面上(披薩)。 但是你也可以使用所有三個空間維度並堆疊它們,這種排列方式稱為“簇”包裝。 即使對於四個球,也可以證明香腸包裝是最優的,因為它需要的體積最小。
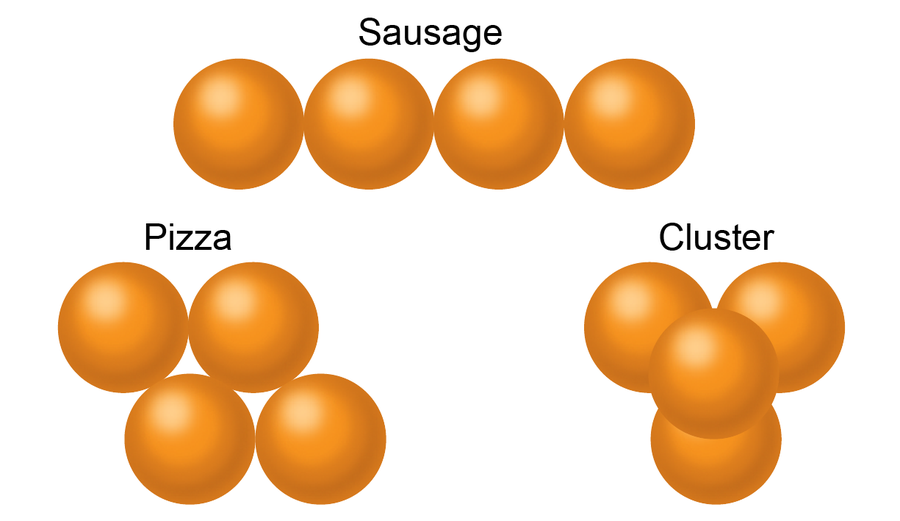
三種可能的包裝排列方式。 來源: Spektrum der Wissenschaft/馬農·比肖夫,由 大眾科學 設計風格
然而,隨著球體數量的增加,事情變得更加複雜。 數學家們推測,香腸包裝對於最多 n = 55 個球是最優的。 但在 1992 年,數學家約爾格·威爾斯和皮爾·馬里奧·甘迪尼確定,對於 56 個球,簇包裝更節省空間。 然而,這個簇到底是什麼樣子尚不清楚。 數學家們能夠找到比球的香腸包裝更好的排列方式——但無法證明它是最優的。 可能存在另一種佔用更少體積的排列方式。
從有序的一維鏈到三維簇的突然轉變在專家圈內被稱為“香腸災難”。 威爾斯和甘迪尼證明,對於 59、60、61 或 62 個球體的排列,以及所有至少包含 65 個球的集合,也最優地形成一個簇。 對於所有其他數量——也就是說,當 n 小於 56 或為 57、58、63 或 64 時——香腸包裝似乎是最優的。 這意味著,對於最多 55 個球,香腸包裝可能是最優的,對於 56 個球,簇包裝是最佳的,而對於 57 或 58 個球,香腸包裝將再次是最節省空間的排列方式。 對於 59、60 或 61 個球體,我們又回到了簇包裝。
這個答案似乎並不特別直觀。 並且沒有人能夠毫無疑問地證明這一點。
訪問 42 維空間
如果數學家們止步於三維,他們就不會成為數學家了。 那麼,n 個四維球體在四維空間中的最佳包裝是什麼樣的呢? 在更高維度中,表示為 d,,區分香腸包裝(一維鏈)、簇包裝(整個 d 維空間中球體的累積)和披薩包裝。 後者代表了其他兩種情況的一種過渡: 它包括球體分佈在超過一個維度且小於 d 維度的所有情況。
事實證明,在四維空間中似乎也存在香腸災難,儘管它發生的比三維情況晚得多。 甘迪尼和他的同事安德烈亞娜·祖科在 1992 年證明,在 d = 4 中,一旦你擁有至少 n = 375,769 個球,簇包裝比香腸包裝更節省空間。
那麼披薩呢? 威爾斯和數學家烏爾裡希·貝特克和彼得·格里茨曼在 1982 年表明,披薩在三維和四維空間中永遠不是最佳包裝。 球體要麼填充整個空間(簇),要麼形成一條線(香腸)。 只有這兩種極端情況才能產生最佳包裝排列。
1975 年,費耶斯·托特表達了他現在著名的針對更高維度的“香腸猜想”。 根據他的說法,香腸包裝對於五維或更高維度中的任何有限數量的球體都是最優的。 即使這個猜想尚未得到最終證明,貝特克和他的同事馬丁·亨克在 1998 年能夠證明,香腸猜想適用於42 個或更多空間維度。
簡而言之,如果你要贈送 42 維橙子作為聖誕禮物,最好將它們排成一排。 並且,如果像最初的問題一樣,你只是贈送五個這樣的三維水果,那麼香腸式包裝將是完美的。
現在想象一下,當你不想包裝橙子而是恐龍玩具或娃娃時,任務變得多麼複雜。 禮品包裝顯然是一個充滿數學謎題的領域。
本文最初發表於《明鏡週刊》 並經許可轉載。
