幾何與不公正劃區

不公正劃區正在全國各地的法庭和頭條新聞中蔓延。美國最高法院最近聽取了關於威斯康星州共和黨和馬里蘭州民主黨選區合憲性的案件，這些選區據稱鞏固了他們的強大優勢，但在兩起案件中都避開了直接裁決。北卡羅來納州的另一起黨派不公正劃區案件正在上訴中，8月份下級法院的一份措辭強烈的意見書推動了該案件的進展。但到目前為止，要讓大法官們對黨派不公正劃區的法律框架感到滿意一直是不可能的。正如前大法官安東尼·肯尼迪在2004年的一起案件中指出的那樣，部分問題在於，高等法院和下級法院尚未就“可行的標準”來確定什麼是黨派不公正劃區達成一致。這就是全國越來越多的數學家認為我們能夠提供幫助的地方。

兩年前，我和幾個朋友成立了一個工作組，研究幾何學和計算在美國重新劃分選區中的應用。從那時起，“度量幾何與不公正劃區小組”擴大了其範圍和使命，深入參與研究、推廣、培訓和諮詢。全國各地有超過1200人參加了我們的研討會，他們中的許多人已經深入參與到重新劃分選區專案中。我們認為現在是時候進行計算干預了。不公正劃區的數學原理出人意料地豐富——足以開創一個獨立的子領域——而計算能力可以說才剛剛趕上重新劃分選區問題的規模和複雜性。儘管我們小組的技術導向，但我們的中心目標是加強和保護公民權利，我們正在與律師、政治學家、地理學家和社群團體密切合作，在下一次美國人口普查和隨後的重新劃分選區之前建立工具和想法。

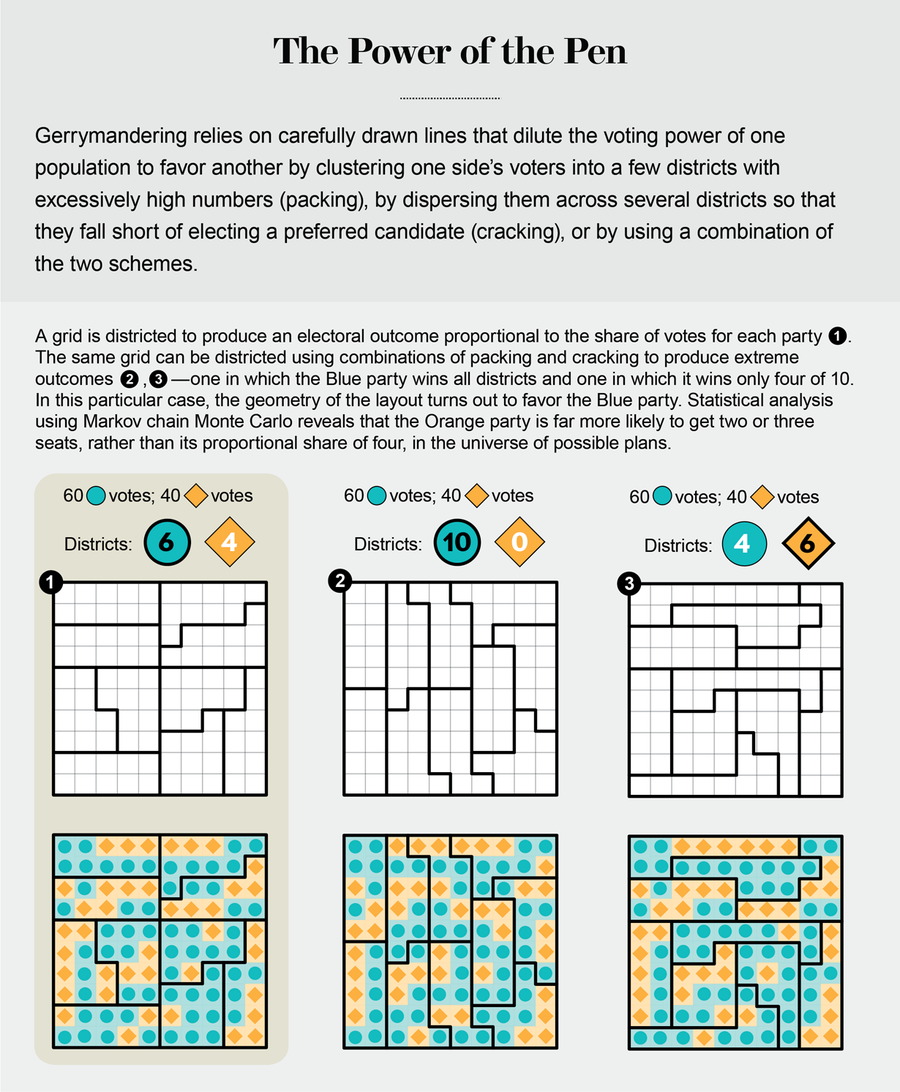
在一個權力掌握在民選代表手中的國家，對於選舉過程的控制權總是會存在衝突。在像我們眾議院這樣的制度中——每個地理選區內勝者全得——選區的劃分是一個天然的戰場。美國曆史上充斥著令人震驚的劃線計劃，從在一個選區塞滿現任議員的忠實擁護者，到將一個歷史悠久的選區切成三塊，以壓制黑人選民的政治權力。許多種類的所謂“集中”和“分散”策略至今仍在繼續，在大資料時代，它們變得異常複雜。現在，比以往任何時候都更難明確地識別出濫用重新劃分選區的行為。人們認為他們透過兩個特徵來了解不公正劃區——怪異的形狀和不成比例的選舉結果——但兩者都不可靠。那麼，我們如何確定天平何時被不公平地傾斜了呢？

支援科學新聞報道

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱，您正在幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。

眼球測試

1812年的事件賦予了我們“不公正劃區”這個詞，它源於這樣一種直覺，即形狀怪異的選區會暴露不合法的意圖。它以當時的馬薩諸塞州州長埃爾布里奇·格里命名。格里擁有相當顯赫的開國元勳血統——《獨立宣言》的簽署人、美國製憲會議的主要參與者、國會議員、詹姆斯·麥迪遜的副總統——因此，考慮到他永恆的名聲來自於不正當的重新劃分選區，這很有趣。“格里-曼德”，或格里的蠑螈，是給波士頓北岸一個彎曲的選區的諷刺性名稱，人們認為這個選區有利於州長的民主共和黨，而不利於競爭對手聯邦黨人。《塞勒姆公報》在1813年刊登了一幅木刻政治漫畫；漫畫中，翅膀、爪子和毒牙被暗示性地新增到選區的輪廓中，以增強其爬行動物般扭曲的外觀。

因此，不規則的選區會暗示我們存在不當行為的觀點由來已久，而緊湊的選區促進民主理想的觀念也與共和國一樣古老。1787年，麥迪遜在《聯邦黨人文集》中寫道，“民主的自然限制是距離中心點的距離，這個距離剛好允許最偏遠的公民儘可能頻繁地聚集，以履行他們的公共職能。”換句話說，選區應該是可通行的。1901年，一項聯邦分配法案首次在美國法律中出現了“選區應由‘緊湊的領土’組成”這一模糊的要求。“緊湊”一詞隨後在重新劃分選區的法律領域中激增，但幾乎總是沒有定義。

例如，在2017年舉行的全國州議會會議上，我瞭解到，在上一次人口普查之後，猶他州的立法者花了值得稱讚的時間和精力建立了一個名為“重新劃分選區猶他州”的網站，向普通公民徵集提議的選區地圖。為了被考慮，地圖必須“合理緊湊”。我抓住機會想弄清楚這個質量是如何被測試和執行的，結果卻得知它只是透過拋棄那些看起來滑稽的地圖來處理的。如果這聽起來很糟糕，那麼猶他州絕非孤例。三十七個州對地圖形狀制定了一些規定，幾乎在所有情況下，眼球測試都是最重要的。

問題在於，選區的輪廓講述的是一個非常片面且常常具有誤導性的故事。一方面，形狀難看肯定有良性的原因。自然地理或合理地嘗試遵循縣界或聯合利益社群可能會影響邊界，儘管同樣常見的是，這些合法的優先事項僅僅是被當作替罪羊，試圖為最令人反感的選區辯護。另一方面，圓潤、矮胖和對稱的選區並不能提供有意義的質量保證。就在今年，賓夕法尼亞州共和黨在州議會起草的一項國會重新劃分選區計劃在賓夕法尼亞州最高法院規定的所有五種公式下都取得了很高的緊湊性得分。然而，數學分析顯示，該計劃仍然會鎖定與2011年制定的扭曲計劃相同的極端黨派偏見，該計劃旨在取代2011年的計劃。因此，法官們選擇了採取非常措施，採納了一項獨立的外部人員的計劃。

失衡的結果

如果形狀不是不公正劃區的可靠指標，那麼研究民選代表與選民投票模式的匹配程度又如何呢？當然，失衡的結果提供了初步的濫用證據。但別急。以我在家鄉馬薩諸塞州的共和黨人為例。自2000年以來，在13次聯邦總統和參議院選舉中，共和黨候選人在全州範圍內平均獲得了超過三分之一的選票。這比在馬薩諸塞州九個國會選區之一中贏得席位所需的水平高出六倍，因為在兩方競爭中，候選人需要獲得簡單多數才能獲勝。然而，自1994年以來，沒有共和黨人在眾議院贏得席位。

我們一定看到了一個不公正劃區，它剝奪了共和黨人理應獲得的席位，對嗎？但這裡的數學完全是開脫罪責的。讓我們看看全州範圍內的競選，這樣我們就可以把無人競爭的席位和其他混淆變數放在一邊。以肯尼斯·蔡斯為例，他是2006年美國參議院泰德·肯尼迪的共和黨挑戰者，他獲得了全州範圍內30%以上的選票。按比例計算，你可能會期望蔡斯在九個國會選區中的近三個選區擊敗肯尼迪。但數字並不符合。事實證明，在州內選擇一個單一的、選區大小的城鎮或選區分組（即使分散在全州各地）來偏愛蔡斯在數學上是不可能的。他的選民根本不夠集中。相反，大多數選區對蔡斯的支援率接近州平均水平，因此沒有足夠的偏愛蔡斯的組成部分來分配。

任何投票少數派都需要一定程度的非均勻性，才能使其選票分佈符合我們的選區劃分選區系統，以便為獲得代表權提供哪怕是理論上的機會。應用於蔡斯-肯尼迪競選的分析甚至沒有考慮空間因素，例如每個選區必須是一個連通整體的標準要求。人們可能會理所當然地懷疑，當各種可能性的前景會帶來如此多的驚喜時，我們如何才能追究選區設計師的責任。

隨機遊走來救援

評估一個選區劃分選區計劃的公正性的唯一合理方法是將其與切割同一管轄區的其他有效計劃進行比較，因為您必須控制選舉結果的各個方面，這些方面是州法律、人口統計和地理因素強制造成的。問題在於，研究可能的計劃宇宙變成了一個難解的大問題。

想象一個簡單的四乘四的網格，假設你想把它分成四個大小相等的連續選區，每個選區有四個正方形。如果我們把網格想象成棋盤的一部分，我們把連續性解釋為車可以在整個選區內訪問，那麼恰好有117種方法可以做到這一點。如果允許角相鄰——所謂的後翼連續性——那麼就有2620種方法。而且它們並不那麼容易計數。正如我的同事、馬薩諸塞大學洛厄爾分校的教授、組合列舉領域的領導者吉姆·普羅普所說，“在一維中，你可以沿著路徑分割來分而治之，但在二維中，突然之間就有很多很多種從A點到B點的方法。”

問題在於，最好的計數技術通常依賴於遞迴——也就是說，使用一個類似的、規模小一步的問題來解決問題——但是二維空間計數問題在沒有一些額外的結構的情況下，遞迴效果不佳。因此，完整的列舉必須依賴於蠻力。雖然一臺巧妙程式設計的筆記型電腦幾乎可以立即對小網格的分割槽進行分類，但隨著網格尺寸的增長，我們看到了複雜性的巨大飛躍，這項任務很快就變得遙不可及。當您到達九乘九的網格時，等數車的分割槽有超過700萬億個解，即使是高效能計算機也需要一週的時間才能將它們全部計數。這看起來像是絕望的境地。我們試圖評估一種切割州的方式，但沒有任何能力來列舉——更不用說有意義地將其與——替代方案的宇宙進行比較。這種情況聽起來像是在黑暗、無限的荒野中摸索。

好訊息是，在科學領域中，有一個行業標準用於處理如此龐大的任務：馬爾可夫鏈蒙特卡羅（MCMC）。馬爾可夫鏈是隨機遊走，其中下一步的去向由機率控制，僅取決於您現在的位置（在每個位置，您擲骰子選擇一個相鄰空間移動）。蒙特卡羅方法只是透過隨機抽樣進行估計。將它們放在一起，您就得到一個強大的工具，用於搜尋廣闊的可能性空間。MCMC已成功用於解碼監獄資訊、探測液體的性質和相變、為困難的計算問題找到可證明準確的快速近似值等等。著名統計學家珀西·戴康尼斯在2009年的一項調查中估計，MCMC推動了科學、工程和商業領域10%到15%的統計工作，而且這個數字可能只會從那時起上升。儘管重新劃分選區中的計算分析可以追溯到幾十年前，但認真嘗試將MCMC應用於這項工作直到2014年左右才開始公開出現。

假設網格蘭州的官員聘請您來決定他們立法機構的選區劃分選區計劃是否合理。如果網格蘭州是一個四乘四的正方形網格，並且其州憲法要求車連續選區，那麼您就走運了：恰好有117種方法可以生成符合要求的計劃，您可以檢查所有這些計劃。您可以使用117個節點來表示有效的計劃，並在節點之間新增邊來表示簡單的移動，其中網格中的兩個正方形交換其選區分配，從而建立這個選區劃分選區計劃宇宙的完美忠實模型。這些邊為您提供了一種概念化兩個計劃有多相似的方法，只需計算將一個計劃轉換為另一個計劃所需的交換次數。（我將這種結構稱為“元圖”，因為它是一個切割另一個圖的方式的圖。）現在假設州立法機構由鑽石黨控制，其競爭對手懷疑它已經操縱了席位以支援自己。為了確定這是否屬實，可以求助於選舉資料。如果鑽石計劃在上次選舉中為該黨產生的席位比方說117個備選方案中的114個更多，並且在之前的幾次選舉中也是如此，那麼該計劃顯然是一個統計異常值。這是黨派不公正劃區的有力證據——而您不需要MCMC來進行這樣的分析。

當您遇到一個完整規模的問題來代替這個小型玩具問題時，MCMC方法就會發揮作用。一旦您超過100個左右的節點，就會出現一個類似的元圖，但您無法完全構建它，因為它具有令人望而生畏的複雜性。但這並不是什麼大問題。從任何一個計劃來看，透過執行所有可能的移動來構建區域性鄰域仍然很容易。現在您可以走一百萬步、十億步或萬億步，看看您發現了什麼。背景中有數學原理（確切地說，是遍歷理論）保證，如果您隨機遊走足夠長的時間，您收集的地圖集合將具有代表總體宇宙的屬性，通常在您甚至訪問過州空間中一小部分節點之前很久。這使您可以確定您正在評估的地圖是否是根據各種黨派指標的極端異常值。

科學探索的前沿是構建更強大的演算法，同時設計新的定理來證明我們的抽樣足夠好，可以得出可靠的結論。圍繞這種方法正在形成一種新興的科學共識，但也存在許多正在進行的研究方向。

R.I.P. 格里州長

到目前為止，法院似乎對這種方法表示讚許。杜克大學的喬納森·馬廷利和卡內基梅隆大學的韋斯·佩格登兩位數學家最近分別就北卡羅來納州的聯邦案件和賓夕法尼亞州的州級案件的MCMC方法作證。

馬廷利使用MCMC來描述人們可能在各種選區劃分選區計劃集合中觀察到的各種指標（例如贏得的席位）的合理範圍。他的隨機遊走被加權，以偏愛那些被認為更接近理想的計劃，這與北卡羅來納州法律的思路一致。利用他的集合，他認為已頒佈的計劃是一個極端的黨派異常值。佩格登使用了一種不同型別的測試，借鑑了一個嚴格的定理，該定理量化了一箇中立計劃的得分比隨機遊走訪問的其他計劃差得多的可能性有多小。他的方法產生p值，這限制了偶然發現這種異常偏差的可能性有多大。法官們認為這兩種論點都是可信的，並在各自的判決中讚賞地引用了它們。

就我而言，賓夕法尼亞州州長湯姆·沃爾夫今年早些時候聘請我擔任諮詢專家，為該州在其最高法院決定推翻2011年共和黨計劃後，爭先恐後地劃定新的選區界限。我的貢獻是使用MCMC框架來評估提出的新計劃，利用統計異常值的力量，同時增加新的方法來考慮更多的各種選區劃分選區原則，從緊湊性到縣分割再到社群結構。我的分析與佩格登的分析一致，都將2011年的計劃標記為極端的黨派異常值——我發現州立法機構提出的新計劃也同樣極端，而其外觀的改善並不能解釋這一點。

隨著2020年人口普查的臨近，全國正在為新一輪瘋狂的重新劃分選區做好準備，隨之而來的是訴訟的承諾。我希望接下來的步驟不僅會在法庭上進行，也會在改革措施中進行，這些措施要求在使用開源工具製作的大量地圖被審查後，才能簽署任何計劃成為法律。這樣，立法機構保留了他們委託和批准選區邊界的傳統特權，但他們必須提供一些保證，確保他們不會在天平上放上太重的砝碼。

計算永遠不會為我們做出艱難的重新劃分選區決定，也無法產生最優的公平計劃。但它可以證明一個計劃的行為就像是從既定的規則中選擇出來的一樣。僅此一點就可以控制最惡劣的濫用行為，並開始恢復對系統的信任。

*編者注（10/23/18）：由於資料變化，表格“如何比較無數的選區劃分選區計劃”的中間和右列中的一些數字在釋出後進行了調整，與11月印刷版《大眾科學》中出現的版本不同。