數學愛好者的福利：生命遊戲創造者約翰·康威的一些謎題

2020 年 4 月 11 日，約翰·霍頓·康威因新冠肺炎在新澤西州新不倫瑞克去世，享年 82 歲。這位傑出的數學家研究領域包括群論、紐結理論、幾何學、分析學、組合博弈論、代數學、演算法學，甚至理論物理學。

康威的興趣和天賦使他發明了一種名為“生命遊戲”的非凡的細胞自動機，在 50 年後仍然令人著迷。康威還設計了精巧的謎題，用於包裝只能透過巧妙的推理才能有效解決的積木盒。

康威認為，他最重要的貢獻是對一個

關於支援科學新聞報道

如果您喜歡這篇文章，請考慮支援我們屢獲殊榮的新聞報道，方式是 訂閱。透過購買訂閱，您將幫助確保未來能夠繼續推出關於塑造當今世界的發現和想法的具有影響力的報道。

被稱為超現實數的奇妙數字系統的概念化。這個類別包括整數、實數、超限數和無窮小——這是一個以前沒有人想象過可能存在的結構，其中一切都可以相加、相乘等等。

與康威共事過的人報告說，他思維非常敏捷，以至於他剛聽到一個問題，往往就已經有了解決方案。康威對面向所有人的數學的執著，促使他研究令休閒數學愛好者感到愉悅的謎題，例如著名的考拉茲猜想（本文末尾將討論該猜想）。

康威是在我的《科學》雜誌法語版《Pour la Science》專欄中被引用次數最多的數學家（超過 30 次！）。在準備文章時，我經常會遇到他證明的結果或他在該主題上率先提出的重要想法，這讓我非常驚訝。康威喜歡簡單、實用的數學問題，這些問題需要發揮他的創造力。

在我看來，紀念他的最好方式是突出那些讓他驚歎和著迷的數學。我將介紹康威做出貢獻的幾個不同主題。但是，要充分展現這位非凡的思想家的才華，需要寫幾卷書才行。他能夠在許多不同的領域發明物體和問題，並解決最棘手的難題，構思出無人能想到的方法。

√2 的無理數性

最令人驚訝和重要的數學發現之一是 2 的平方根 (√2) 的無理數性——邊長為 1 個單位的正方形的對角線的長度。 它不能用正整數 n 和 m, 的商或 n/m 來表示。√2 的無理數性的發現歸功於畢達哥拉斯或他的弟子之一，儘管我們不知道其背後的推理是算術的還是幾何的。這一發現及其證明對數學家來說是極其令人不安的。數學中的第一個負面發現表明，人類並沒有創造支配數字的定律，而是在探索未知的數學領域時揭示了這些定律。

儘管有許多定理證明，但最直觀的是康威在 2005 年出版的一本書中的講座中包含的一個非常簡單的簡圖。  他將這個證明的建立歸功於數學家斯坦利·泰嫩鮑姆，據康威說，他已經放棄了數學。您可能會問，這個證明是否是康威自己提出的。但這並不重要。因為即使不是他創造的，這個證明也完美地體現了康威的數學方法，他在 100 種不同的方式中都展示了這種方法。它還表明，認為一切簡單的事物都已被發現是錯誤的：輝煌而又出奇簡單的想法仍在等待被揭示。

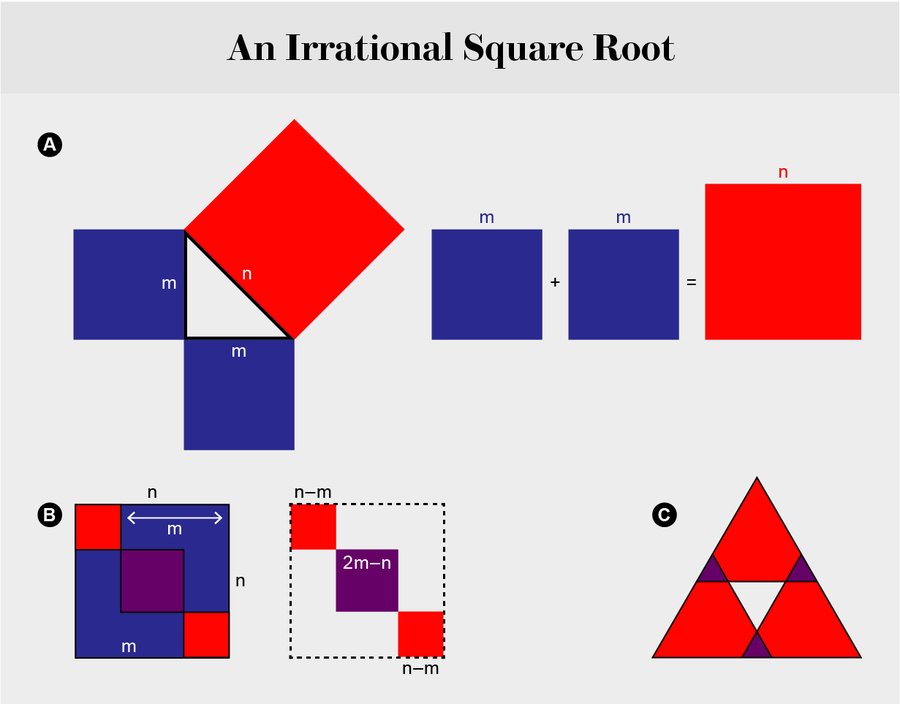
假設 √2 是 n 和 m 的商——也就是說，2 = n²/m², 或 2m² = n²。如果是這樣，則存在一個邊長等於 n 的正方形，其面積等於邊長等於 m 的正方形的兩倍 [參見“無理平方根”的 A 部分]。我們假設在我們的圖中，m 是滿足此方程的最小正整數。只有在沒有更小的正整數滿足它時，該假設才有效。

將兩個藍色正方形楔入紅色正方形的兩個對角角落會產生一個新的形狀。該形狀中的兩個紅色正方形的面積必須與兩個藍色正方形重疊處建立的中心紫色正方形的面積相同 [參見“無理平方根”的 B 部分]。

我們的推理要求兩個藍色正方形的面積必須等於紅色正方形的面積 (A)。因此，未被兩個藍色正方形覆蓋的面積等於兩者覆蓋的面積的兩倍。換句話說，有兩個相等且較小的正方形（紅色，B），它們加在一起的面積與較大的正方形（紫色，B）相同。這意味著新的小正方形的每條邊都等於整數 n – m，而大的紫色正方形的每條邊都等於整數 n – 2(n – m) = 2m – n。

簡而言之，邊長為 m 的初始正方形不是滿足幾何方程的最小正方形。結果是一個矛盾，因此假設是錯誤的：√2 不是兩個整數的商，這意味著它是一個無理數。以同樣的方式，您可以證明 3 的平方根是無理數 [參見“無理平方根”的 C 部分]。

三個立方體堆疊謎題

許多謎題包括將少量積木放入盒子中（例如 10 個）。積木和盒子通常都是長方體。解決方案通常是透過反覆試驗得出的。對於這樣的問題，除非您增加積木的數量及其形狀的多樣性，否則很難構思出一個具有挑戰性的謎題。此外，儘管在找到解決方案之前操作積木可能很有趣，但這樣做只涉及到對形狀的少量推理，因此並沒有真正減少解決時間。

康威重新構想了這個問題，創造了可能會讓您在嘗試找出如何填充盒子時陷入迴圈的謎題。但是，一些精明而有條不紊的考慮將很快引導您找到解決方案。

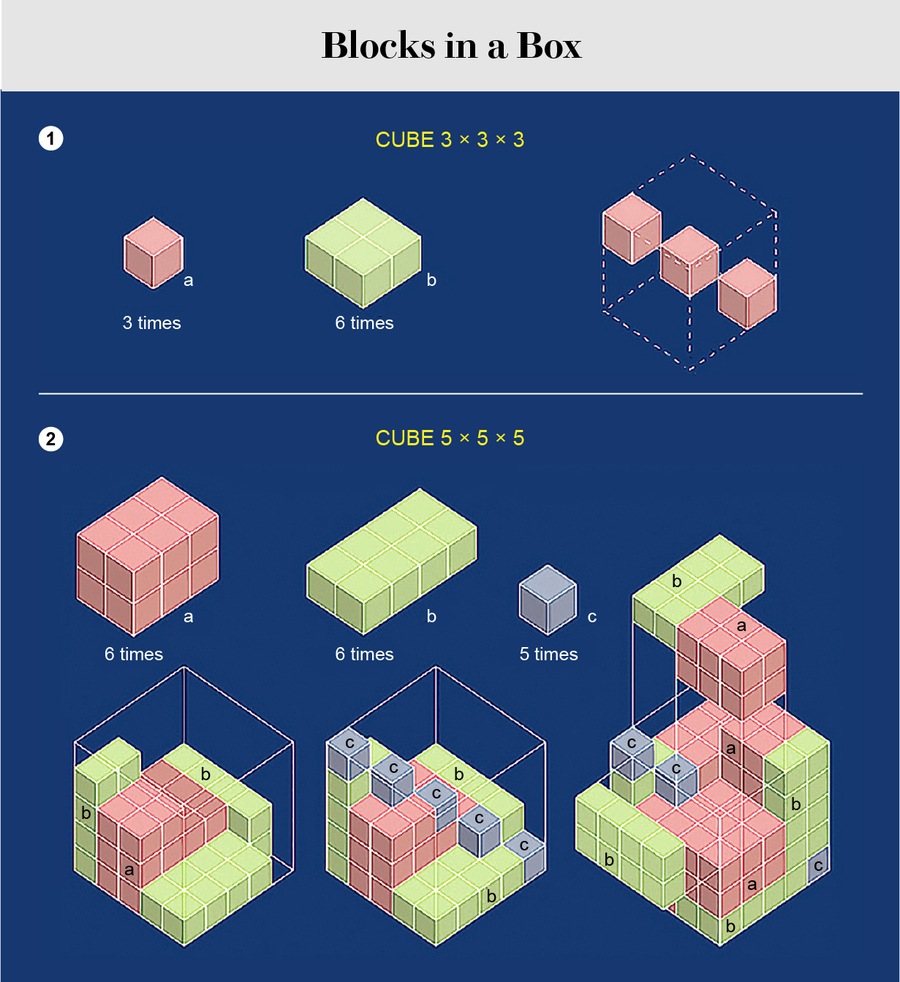
這三個謎題中最簡單的一個是用三個 1 x 1 x 1 的立方體和六個 1 x 2 x 2 的長方體填充一個 3 x 3 x 3 的盒子 [參見“盒子裡的積木”的第 1 部分]。

推理包括考慮奇偶性：3 x 3 x 3 的盒子由三個水平的 3 x 3 x 1 層組成，每層的體積為 9。3 x 3 x 3 的盒子也可以分解為三個垂直的 3 x 3 x 1 長方體，每個長方體平行於盒子的一個垂直面。考慮垂直面產生盒子分解為三個 3 x 3 x 1 長方體的第三種分解方式。

讓我們檢查一下這九個長方體。當一個 1 x 2 x 2 的積木放置在盒子中時，它只能填充每個 3 x 3 x 1 層中九個單元格的偶數個。因此，每一層都必須包含三個小的 1 x 1 x 1 積木中的一個——且僅一個——（否則您必須將所有三個都放在一個 3 x 3 x 1 層中，這將導致其他兩層中沒有，而它們是需要的）。因此，盒子的頂層必須包含一個 1 x 1 x 1 的積木。如果我們將它放在該層的中心，我們很快就會陷入僵局，因為我們不得不將另一個小積木放在它的正下方。這將它們中的兩個放在一個 3 x 3 x 1 的垂直層中。將頂面上的小積木放在任何一側的中間也會導致僵局。因此，頂層上的小積木必須放在一個角上。

同樣的推理適用於底層，底層上的小積木也必須放在一個角上。那個角必須與頂層上的小積木對角相對。因此，第三個小積木必須放在中間層的中心。剩下的步驟很快就變得顯而易見了。請注意，這種推理不僅產生了解決方案，而且還表明，除了對稱性之外，只有一個解決方案。

康威的另一個堆疊問題（“盒子裡的積木”的第 2 部分）中顯示瞭解決方案。要完成堆疊，您只需降低兩個上部結構，並將綠色層 (b) 放在粉色層 (a) 上方的側面即可。基於奇偶性的推理迫使我們將單位立方體沿對角線放置。

兩個巫師的謎題

在 20 世紀 60 年代，康威設計了一個極其棘手的謎題，直到最近，該謎題還引發了許多爭論，並且麻省理工學院的塔尼婭·霍瓦諾娃在 2013 年發表了一篇論文。以下是該論文中出現的謎題

昨晚我坐在公共汽車上的兩位巫師後面，無意中聽到以下對話

巫師 A：“我有幾個正整數個孩子，他們的年齡都是正整數，他們的年齡之和是這輛公共汽車的號碼，而他們的年齡之積就是我的年齡。”

巫師 B：“真有趣！也許如果您告訴我您的年齡和孩子的數量，我可以算出他們每個人的年齡？”

巫師 A：“不。”

巫師 B：“啊哈！我終於知道您多大了！”

那麼，公共汽車的號碼是多少？

請注意，在對話中，巫師 A 說的“不”並不意味著他拒絕回答，而是意味著知道他的年齡和孩子的數量並不能知道他們每個人的年齡。當然，您必須假設巫師 B 知道公共汽車的號碼。還要注意，巫師可能非常年輕或非常年老：巫師 A 很可能只有兩歲或兩萬歲。

這是解決方案，我只能在程式的幫助下完全理解和驗證它。我無法重現得出結論所需的所有計算，但您可以相信我的話，或者重新進行我遺漏的所有計算。

讓我們將巫師 A 的年齡表示為 a，公共汽車的號碼錶示為 b，巫師 A 的孩子的數量表示為 c。例如，假設公共汽車的號碼是 b = 5。以下是孩子數量、年齡分佈和巫師 A 年齡的選項

• c = 5 個孩子，年齡分別為 1、1、1、1、1；因此，a = 1；

• c = 4 個孩子，年齡分別為 1、1、1、2；因此，a = 2；

• c = 3 個孩子，年齡分別為 1、1、3；因此，a = 3；

• c = 3 個孩子，年齡分別為 1、2、2；因此，a = 4；

• c = 2 個孩子，年齡分別為 1、4；因此，a = 4；

• c = 2 個孩子，年齡分別為 2、3；因此，a = 6；

• c = 1 個孩子，年齡為 5；因此，a = 5。

在每種情況下，知道巫師 A 的年齡和孩子的數量都可以指示後者的可能年齡。由於巫師 A 回答“不”，並且巫師 B 知道公共汽車的號碼，這意味著 b 不等於 5。

同樣，您可以透過逐個檢查可能的公共汽車號碼來解決問題，以找到那些知道巫師的年齡和孩子的數量也不能讓您知道每個孩子的年齡的號碼（我們將其表示為屬性 P）。計算 b = 1、2、3、...、12（正如我們剛剛對 b = 5 所做的那樣）表明，b = 12 是具有屬性 P 的最小數字。

實際上，對於 b = 12 和 c = 4，有兩組可能的四個孩子的年齡——(2, 2, 2, 6) 和 (1, 3, 4, 4)——它們都給出了相同的巫師 A 年齡：a = 48。對於 b = 12，不存在其他兩個長度相同且乘積相同的集合。因此，對於 b = 12，即使知道 c = 4 和 a = 48，也不可能推斷出四個孩子的年齡。這是否意味著 b = 12 是解決方案？

不幸的是，還不是。例如，對於公共汽車號碼 b = 13，因為兩組可能的三個孩子的年齡——(1, 6, 6) 和 (2, 2, 9)——都與 a = 36 相容，巫師 B 無法從知道他的年齡或孩子的數量中推匯出巫師 A 的孩子的年齡。

知道 b = 12 並不比知道 b = 13 更能確定孩子的年齡。當面對這個謎題時，大多數人通常會回答“b = 12”，就好像這個謎題以某種方式暗示最小可能的 b 解決方案是正確的解決方案。但是，該謎題並沒有做出這樣的斷言。此外，如果沒有進一步的推理，您無法在 b = 12 和 b = 13 之間做出選擇，也無法在其他 b 值之間做出選擇，正如我的進一步計算表明的那樣。

然而，b = 12 是正確的答案，而原因在於謎題中最有趣和最出乎意料的部分。康威精心設計了他的謎題，您必須考慮巫師 B 的最後陳述。在巫師 A 說“不”之後，巫師 B 回答說：“啊哈！我終於知道您多大了！” 這排除了 b = 13。

事實上，對於 b = 13，還有另外兩組孩子的年齡——(1, 2, 2, 2, 6) 和 (1, 1, 3, 4, 4)——它們都給出了 a = 48。換句話說，如果公共汽車號碼是 13，巫師 B 就無法從他的否定回答中推斷出巫師 A 的年齡，因為他的年齡可能是 36 或 48。因此，應該排除 b = 13。

然而，排除 b = 13 會導致排除 b = 14，當我們考慮為 b = 13 找到的年齡序列並加 1 時。這樣做表明，兩組孩子的年齡——(1, 1, 6, 6) 和 (1, 2, 2, 9)——的乘積是 a = 36，而另外兩組——(1, 1, 2, 2, 6) 和 (1, 1, 1, 3, 4, 4)——的乘積是 a = 48。相同的過程排除了 b = 15，並逐個排除了所有大於 12 的 b。

因此，只有公共汽車號碼 12 (b = 12)，以及兩組孩子的年齡——(2, 2, 2, 6) 和 (1, 3, 4, 4)——才能唯一確定巫師 A 的年齡：a = 48。

鑑於您必須進行所有計算才能得出解決方案——我在這裡沒有重現這些細節，而且這些細節佔據了幾個頁面——我承認我不明白康威是如何構思出這個令人難以置信的謎題的！

用線段鋪滿平面

用正方形鋪滿平面很容易。用等邊三角形或六邊形這樣做也很容易。也可以用無限條直線鋪滿平面：只需將它們並排平行放置即可。將有無數條直線，但鋪滿效果將非常令人滿意，因為平面的每個點都將屬於鋪滿線中的一條——且僅一條。以下是一些更棘手的問題

• 平面可以用閉合線段鋪滿嗎？即包括端點的直線線段 [A, B]？

• 平面可以用開放線段鋪滿嗎？即不包括端點的線段 ]A, B[？

• 平面可以用半開放線段鋪滿嗎？即僅包含一個端點的線段 ]A, B]？

思考一下這些不尋常但又完全自然的問題。它們並非如此簡單。康威和一位同事在 1964 年發表的一篇精彩論文中討論了這些問題和其他型別的問題，再次證明了沒有人思考過的非常簡單的問題是進行不太明顯的數學運算的絕佳機會。

在該論文中，康威和數學家哈拉德·克羅夫特設計了一種用直線線段填充平面的方法，這可以在下面的“精細鋪路”中看到。

面板 a 顯示瞭如何用半開放線段鋪滿平面，其中包含一個點，而另一個點被排除在外。這樣做很容易，因為將它們首尾相連地放置在一起，就可以重現用直線進行的明顯鋪路。

面板 b 顯示了相等閉合線段的解決方案，其中每個線段的兩個點都包含在內。首先放置支柱 1。然後新增支柱 2，但當然不保留此堆疊的最左側線段。對於支柱 3，不保留最右側線段。連續新增越來越精細的傾斜支柱，省略每個支柱的“第一個”線段。

面板 c 顯示了不同尺寸的開放線段（其端點被排除在外）的解決方案。這些線段建立了一箇中心正方形，該正方形在所有側面都是開放的——即，正方形的邊和頂部或底部都沒有被覆蓋。每個連續新增的矩形也是開放的。對於相同長度的開放線段，沒有鋪滿平面的解決方案。

考拉茲猜想

另一個謎題對於業餘數學家和專業人士都同樣有趣。考慮一個函式 (f)，該函式對於正偶數整數 (n) 給出 n/2，對於正奇數整數 (n) 給出 3n + 1。例如，從 7 開始並應用 f，您得到 22，然後是 11、34、17、52、26、13、40、20、10、5、16、8、4、2、1、4、2、1，依此類推。一旦您到達 1，您就會繞圈打轉。

無論您從哪個整數 n 開始，您似乎總是最終到達 1，然後陷入迴圈。 計算機計算已經測試了此屬性，對於至少高達 87 x 2⁶⁰（約 10²⁰）的所有 n 都為真。然而，尚未證明情況總是如此，也未找到會繼續延伸到無窮大或導致 4、2、1 以外的迴圈的初始 n。

這個問題被稱為考拉茲猜想或錫拉丘茲猜想。已經投入了大量工作來研究它，其中一些工作已彙編成一本書。該問題陳述的極大簡潔性吸引了業餘愛好者，我經常收到提出的解決方案，但迄今為止，這些解決方案要麼是錯誤的，要麼是無法理解的。

面對這樣一個挑戰——如此簡單地陳述但尚未解決，80 多年後仍然如此——康威無法抗拒。

1972 年，他發表了關於該主題的第一篇論文，其中他提出了類似表述的問題，並證明了它們的不可判定性。對於起始整數的某些值，由 f 的變體生成的序列不會最終到達 1，但集合論無法證明這一點。更一般地，對於任何邏輯證明系統 (S)，都存在此類別的問題以及一個序列的起點，該序列不會最終到達 1，而這無法被 S 證明。

2013 年，康威使用機率論證重新研究了這個問題，表明考拉茲猜想本身對於數學中常用的公理系統來說是不可證明的。這不是對考拉茲猜想的不可判定性的最終證明。但是，他提出的論證型別似乎強烈表明，每個人在嘗試證明該猜想時都會遇到困難並非偶然。

所有數學家都會遇到他們無法解決的問題，康威也不例外。然而，他作為邏輯學家的技能可能提供了一些安慰，使他能夠證明不可判定性並闡述論點，表明這個簡單但棘手的問題將無限期地繼續挑戰數學家。

生命遊戲中的新模式

生命遊戲於 1970 年首次在馬丁·加德納的《大眾科學》雜誌的“數學遊戲”專欄中介紹，至今仍在研究中，它提出的所有謎題尚未解決。無限二維矩形網格中的正方形單元格可能是活著的或死亡的。或者，單元格可能會從活著（黑色）變為死亡（白色），反之亦然，從一代到另一代。或者，單元格可能會保持穩定，具體取決於其八個最近鄰單元格是死亡還是活著。

演化規則可以用 12 個字來表達：如果有三個活著的鄰居則出生；如果有兩個或三個活著的鄰居則生存。初始狀態下只有少量活細胞的一些模式會增長到無限大。理想情況下，活細胞的數量與 n² 成正比增加，其中 n 是世代數。網格穩定部分中活細胞的最佳密度為 1/2。哈佛大學的諾姆·埃爾基斯在 1997 年用 29 頁證明了這一點。

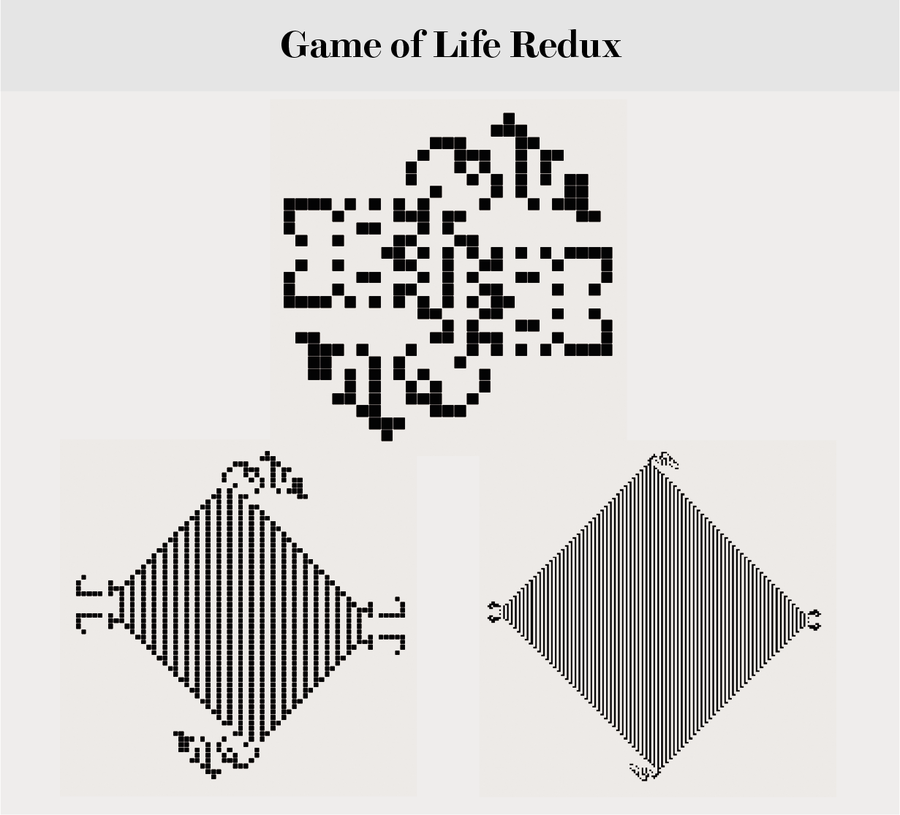
“生命遊戲重製版”頂部顯示的非凡模式是由計算機科學家馬特烏什·納希謝夫斯基於 2020 年 4 月發現的。它是已知的最小模式，一旦啟動，就會呈二次方增長，以覆蓋密度為 1/2 的穩定活細胞群體的網格。（因此，這種模式在速度和密度方面是最佳的。）配置以 183 個單元格的群體開始。我們繪製了第 0 代和另外兩個不同比例的世代 [參見“生命遊戲重製版”中的底部模式]。據信不可能做得比 183 個更好，但這尚未得到證明。還要注意，有些模式可以計算素數，甚至可以顯示 π = 3.14159... 的十進位制數字的圖形影像，一個接一個。

本文最初發表在《Pour la Science》雜誌上，經許可轉載。