編者按:本文發表於1956年,非常受歡迎,啟發了馬丁·加德納的傳奇《大眾科學》專欄《數學遊戲》。在我們的特別數字期刊《樂趣與遊戲》中閱讀更多內容。
數學在很大程度上歸功於遊戲,反之亦然。有一個引人入勝的小練習,用紙條進行,近年來吸引了一些一流的頭腦。它是一位在普林斯頓大學的英國數學系學生在閒暇時發現的。整件事源於一個微不足道的情況,即英國和美國的筆記本紙張尺寸不同。亞瑟·H·斯通,一位23歲的英國研究生,於1939年秋季獲得獎學金來到普林斯頓,他發現自己必須從美國筆記本紙上修剪掉一英寸,才能將它們放入他的英國活頁夾中。為了消遣,他開始以各種方式摺疊修剪下來的紙條,他製作的一個圖形結果特別有趣。他將紙條在三個地方斜向摺疊,並將兩端連線起來,使其成為一個六邊形[見下圖插圖]。當他將兩個相鄰的三角形捏合在一起,並將六邊形相對的頂點推向中心時,六邊形會像含苞待放的花朵一樣再次張開,並顯示出一個全新的面。例如,如果原始六邊形的頂面和底面被塗成不同的顏色,那麼新出現的面將是空白的,而其中一個彩色面將消失!
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
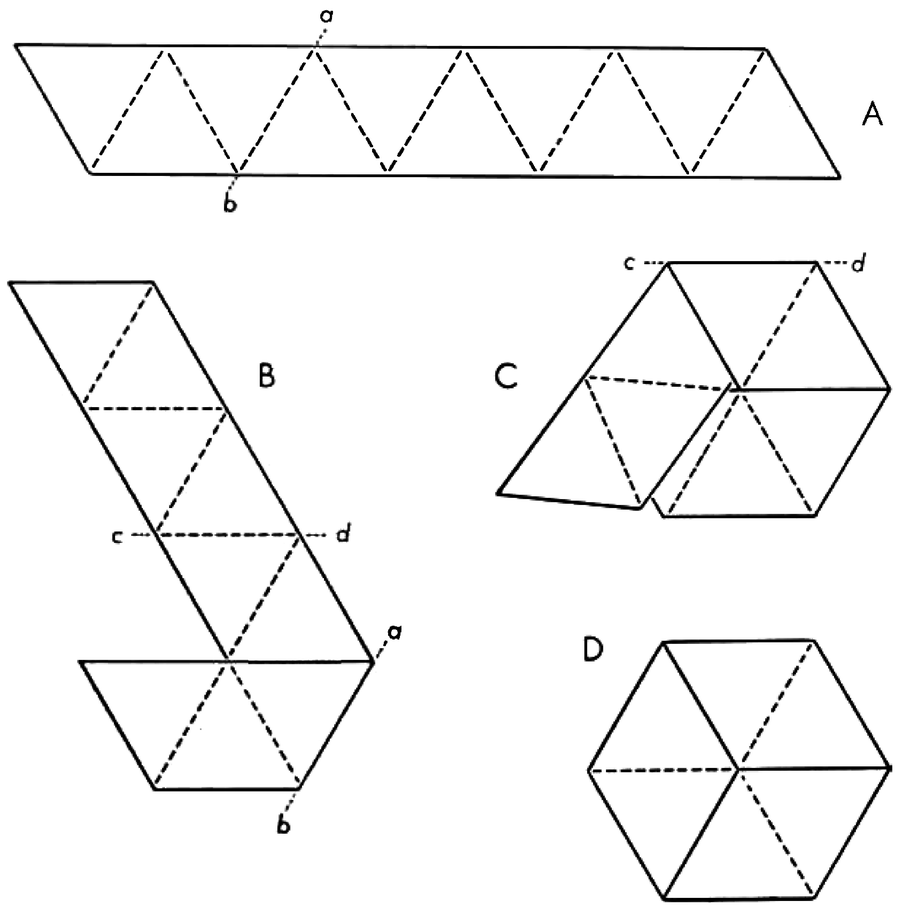
三六邊柔韌環是由切割紙條製成的,使其可以標記為10個等邊三角形(A)。紙條沿線ab向後摺疊並翻轉(B)。然後再次沿線cd向後摺疊,並將倒數第二個三角形放在第一個三角形的頂部(C)。現在將最後一個三角形向後摺疊並貼上到第一個三角形的另一側(D)。該圖形可以如下圖所示彎曲。它不是要被剪下來的。建議使用至少一英寸半寬的相當硬的紙張。
文治·田川
這個圖形有三個面——比如,紅色、綠色和空白。斯通進一步試驗了更長的紙條,並且憑藉相當的耐心和創造性的洞察力,他能夠構建一個模型,該模型具有相同的六邊形形狀,但可以開啟到六個不同的面,而不是隻有三個。在這一點上,斯通發現這個遊戲非常有趣,以至於他向研究生院的朋友展示了他的紙模型。“柔韌環”很快就在午餐和晚餐桌上大量湧現。組織了一個“柔韌環委員會”,以進一步探究柔韌環的奧秘。除了斯通之外,其他成員還有數學研究生布萊恩特·塔克曼;物理學研究生理查德·P·費曼;以及年輕的數學講師約翰·W·圖基。
這些模型被命名為六邊柔韌環——“hexa”代表構成六邊形面的六個三角形,“flexagon”代表結構的彎曲能力。斯通的第一個模型是三六邊柔韌環(“tri”代表可以顯示出來的三個不同面);他優雅的第二個結構是六六邊柔韌環(代表它的六個面)。
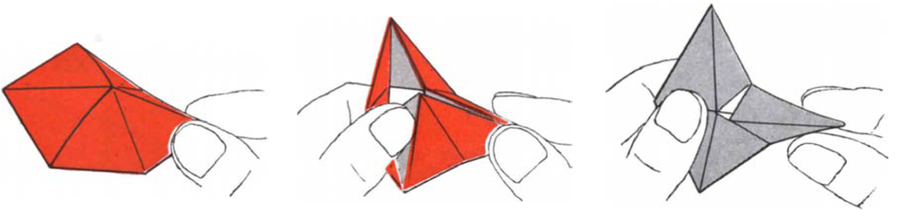
三六邊柔韌環透過捏合其兩個三角形來彎曲。可以用另一隻手開啟兩個相對三角形的內邊緣(中間)。如果圖形無法開啟,則捏合相鄰的一對三角形。如果圖形開啟,則可以將其翻轉過來,露出之前不可見的一側。
文治·田川
要製作六六邊柔韌環,您需要從一張紙條開始(加法機中使用的紙帶非常適用),該紙條被分成19個三角形[見下圖插圖]。您在一側的三角形上編號1、2和3,將第19個三角形留空,如圖所示。在三角形的另一側,根據所示方案編號為4、5和6。現在您摺疊紙條,使相同的底面數字彼此相對——4對4,5對5,6對6,依此類推。由此產生的摺疊紙條,如下圖中的第二個圖所示,然後線上ab和cd上向後摺疊[插圖中的第三個圖],形成六邊形[插圖中的第四個圖];最後,將空白三角形翻轉到下方並貼上到紙條另一側的相應空白三角形上。所有這些用標記好的紙條進行比描述更容易執行。
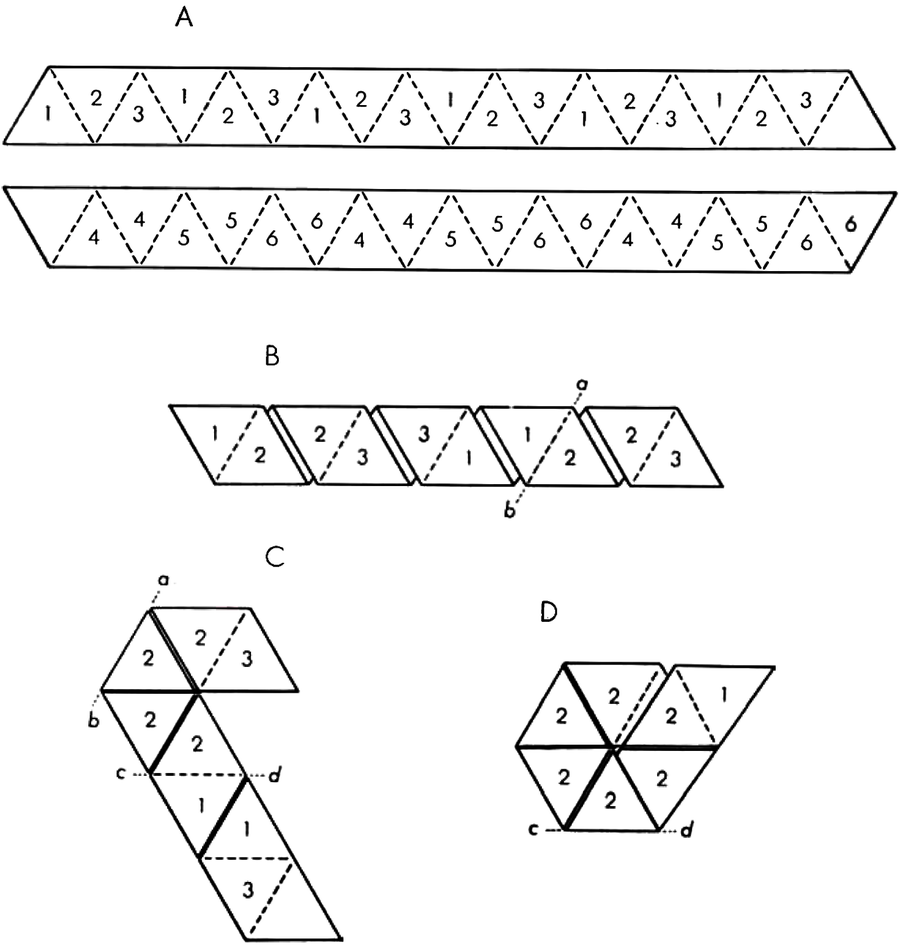
六六邊柔韌環是由切割紙條製成的,使其可以標記為19個三角形(A)。一側的三角形編號為1、2和3;另一側的三角形編號為4、5和6。也可以使用類似的顏色或幾何圖形圖案。然後如圖所示摺疊六邊形。該圖形可以彎曲以顯示六個不同的面。
文治·田川
如果您正確地進行了摺疊,則六邊形的一個可見面上的三角形都編號為1,而另一面上的三角形都編號為2。您的六六邊柔韌環現在可以彎曲了。您將兩個相鄰的三角形捏合在一起,沿著它們之間的線彎曲紙張,然後推入相對的頂點;然後圖形可能會開啟以顯示面3或5。透過隨機彎曲,您應該能夠毫不費力地找到其他面。面4、5和6比1、2和3更難揭示。有時您可能會發現自己陷入一個令人惱火的迴圈中,該迴圈不斷重複返回相同的三個面。
塔克曼很快發現,顯示任何柔韌環的所有面的最簡單方法是保持在同一頂點彎曲它,直到它拒絕開啟,然後轉移到相鄰的頂點。此過程稱為“塔克曼遍歷”,將在12次彎曲的迴圈中顯示六六邊柔韌環的六個面,但1、2和3面出現的頻率是4、5和6面的三倍。

“塔克曼遍歷”在12次彎曲中顯示了六六邊柔韌環的所有六個面。在此,前圖中柔韌環的數字已被相同模式的幾何圖形取代。面1、2和3出現的頻率是面4、5和6的三倍。
文治·田川
委員會發現,透過加長三角形鏈,可以製作具有9、12、15個或更多面的柔韌環:塔克曼設法制作了一個可行的48面模型!他還發現,使用鋸齒形紙條(即,邊緣為鋸齒狀而不是直線的紙條),可以製作四六邊柔韌環(四個面)或五六邊柔韌環。有三種不同的六六邊柔韌環——一種由直紙條摺疊而成,一種由彎曲成六邊形的鏈條摺疊而成,還有一種由有點像三葉草的形狀摺疊而成。十六邊柔韌環(10個面)有82種不同的變體,全部由奇特彎曲的紙條摺疊而成。柔韌環可以形成任意所需的面數,但超過10個面後,每種物種的不同變體數量會以驚人的速度增加。順便說一句,所有偶數面的柔韌環都是由具有兩個不同面的紙條製成的,但具有奇數面的柔韌環只有一個面,就像莫比烏斯曲面一樣。
圖基和費曼在1940年制定了一個完整的柔韌環數學理論。它顯示了除其他外,如何精確地構建任何所需尺寸或種類的柔韌環。該理論從未發表過,儘管此後其他數學家重新發現了其中的一部分。柔韌環研究者中包括塔克曼的父親,傑出的物理學家路易斯·B·塔克曼,他以前在國家標準局工作。塔克曼高階工程師為該理論設計了一種簡單而有效的圖解符號。
珍珠港事件叫停了委員會的柔韌環計劃,戰爭工作很快將四位創始成員分散到各地。斯通現在是英國曼徹斯特大學的數學講師。費曼現在在加州理工學院,是一位著名的理論物理學家。圖基是普林斯頓大學的數學教授,他對拓撲學和統計理論做出了傑出貢獻,這為他贏得了世界範圍的認可。塔克曼是普林斯頓高等研究院的著名數學家,他在該研究院的電子計算機專案上工作。
委員會希望有一天能共同撰寫一兩篇論文,這將是對柔韌環理論的權威闡述。在那之前,我們其他人可以自由地彎曲我們的柔韌環,看看我們自己能發現多少理論。
