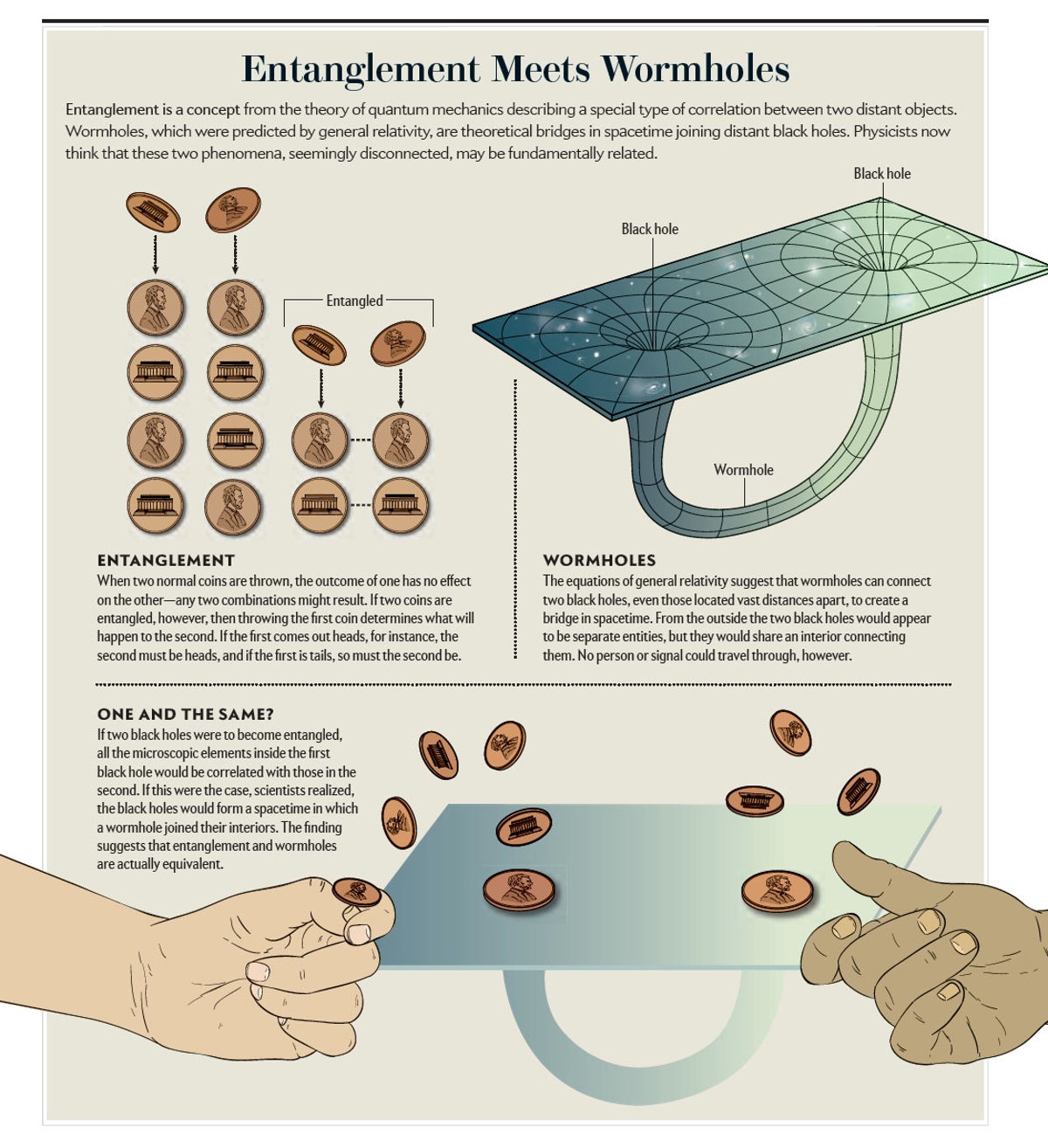
理論物理學充滿了令人難以置信的想法,但其中最奇怪的兩個是量子糾纏和蟲洞。第一個是由量子力學理論預測的,描述了物體(通常是原子或亞原子粒子)之間一種令人驚訝的相關性,這些物體之間沒有明顯的物理聯絡。蟲洞是由廣義相對論預測的,是連線遙遠時空區域的捷徑。包括我自己在內的幾位理論家所做的工作表明,這兩個看似不同的概念之間存在聯絡。基於涉及黑洞的計算,我們意識到量子力學的糾纏和廣義相對論的蟲洞實際上可能是等價的——對相同現象的不同描述——並且我們相信這種相似性適用於黑洞之外的情況。
這種等價性可能具有深遠的意義。它表明時空本身可能從宇宙更基本的微觀組成部分的糾纏中湧現出來。它還表明,長期以來被認為彼此之間沒有物理聯絡的糾纏物體,實際上可能以我們想象不到的方式聯絡在一起。
此外,糾纏和蟲洞之間的關係可能有助於發展量子力學和時空的統一理論——物理學家稱之為量子引力理論——該理論從支配原子和亞原子領域相互作用的定律中推匯出宏觀宇宙的物理學。這種理論對於理解宇宙大爆炸和黑洞內部是必要的。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
有趣的是,量子糾纏和蟲洞都可以追溯到阿爾伯特·愛因斯坦及其合作者在 1935 年撰寫的兩篇文章。從表面上看,這些論文似乎處理的是非常不同的現象,愛因斯坦可能從未懷疑過它們之間可能存在聯絡。事實上,糾纏是量子力學的一個特性,它極大地困擾著這位德國出生的物理學家,他稱之為“幽靈般的超距作用”。多麼諷刺,它現在可能提供一座橋樑,將他的相對論擴充套件到量子領域。
黑洞和蟲洞
為了解釋為什麼我認為量子糾纏和蟲洞可能相關,我們必須首先描述黑洞的幾個特性,這些特性與這個想法密切相關。黑洞是彎曲時空的區域,與我們習慣的相對未扭曲的空間截然不同。黑洞的獨特特徵是我們可以將其幾何形狀分為兩個區域:外部,空間彎曲,但物體和資訊仍然可以逃脫;以及內部,位於不歸路之外。內部和外部被一個稱為事件視界的表面隔開。廣義相對論告訴我們,視界只是一個假想的表面;宇航員穿過它不會在那個位置感覺到任何特殊的東西。但是,一旦穿過它,太空旅行者註定會被擠壓到一個曲率巨大的區域,並且無法逃脫。(事實上,與外部相比,內部實際上是在未來,因此旅行者無法逃脫,因為他或她無法穿越到過去。)
就在愛因斯坦提出廣義相對論一年後,德國物理學家卡爾·史瓦西找到了愛因斯坦方程的最簡單解,描述了後來被稱為黑洞的東西。史瓦西提出的幾何形狀是如此出乎意料,以至於直到 20 世紀 60 年代,科學家們才完全理解它描述的是連線兩個黑洞的蟲洞。從外部看,黑洞似乎是位於遙遠位置的獨立實體,但它們共享一個內部。
在 1935 年的一篇論文中,愛因斯坦和他在普林斯頓高等研究院的同事內森·羅森預料到,這個共享的內部是一種蟲洞(儘管他們不理解它預測的完整幾何形狀),因此蟲洞也被稱為愛因斯坦-羅森(ER)橋。
史瓦西解中的蟲洞與宇宙中自然形成的黑洞不同,因為它不包含物質——它僅僅是彎曲的時空。由於物質的存在,自然形成的黑洞只有一個外部。大多數研究人員將完整的史瓦西解及其兩個外部視為與宇宙中的黑洞無關的數學奇點。儘管如此,這是一個有趣的解,物理學家們一直在思考它的物理意義。
史瓦西解告訴我們,連線兩個黑洞外部的蟲洞隨時間變化。它隨著時間的推移而拉長並變細,就像一塊被拉伸的彈性麵糰。與此同時,曾經接觸過的兩個黑洞視界迅速分離。事實上,它們拉開得如此之快,以至於我們無法使用這樣的蟲洞從一個外部旅行到另一個外部。或者我們可以說,橋樑在我們能夠穿過它之前就坍塌了。在麵糰拉伸的類比中,橋樑的坍塌對應於麵糰在拉伸得越來越多時變得無限薄。
重要的是要注意,我們正在討論的蟲洞與廣義相對論定律一致,廣義相對論不允許超光速旅行。在這方面,它們與科幻小說中的蟲洞不同,科幻小說中的蟲洞允許在遙遠的空間區域之間進行瞬時傳輸,就像 2014 年的電影《星際穿越》中那樣。科幻小說版本通常違反已知的物理定律。
一個涉及我們這類蟲洞的科幻故事可能是這樣的。想象一下一對年輕戀人,羅密歐和朱麗葉。他們的家人不喜歡彼此,因此將羅密歐和朱麗葉放在不同的星系中,禁止他們旅行。然而,這對戀人非常聰明,他們設法構建了一個蟲洞。從外部看,蟲洞看起來像一對黑洞,一個在羅密歐的星系中,一個在朱麗葉的星系中。戀人們決定跳進各自黑洞的內部。現在,根據他們的家人所說,他們只是透過跳進去自殺了,並且再也沒有聽到他們的訊息。然而,不為外界所知的是,蟲洞的幾何形狀是這樣的,羅密歐和朱麗葉實際上在共享的內部相遇了!在橋樑坍塌,摧毀內部並殺死他們之前,他們可以幸福地生活一段時間。
來源:Jillian Ditner
量子糾纏
1935 年討論我們感興趣的另一個現象——糾纏——的論文是由愛因斯坦、羅森和鮑里斯·波多爾斯基(當時也在高等研究院)撰寫的。這三位作者後來被稱為 EPR。在這項著名的工作中,物理學家們認為,量子力學允許在遙遠的物理物體之間存在某些奇怪的相關性,這種特性直到後來才被稱為糾纏。
遙遠物體之間的相關性也可能發生在經典物理學中。例如,想象一下你只有一個手套在身上,因為你把另一隻忘在家裡了。在搜尋你的口袋之前,你不知道你擁有的是左手手套還是右手手套。但是,一旦你看到你擁有的是右手手套,你就會立即知道家裡的那隻手套是左手的。但是,糾纏涉及一種不同的相關性,一種存在於受量子力學支配的量之間的相關性,這些量受海森堡不確定性原理的約束。該原理指出,有些物理變數對不可能同時精確知道。最著名的例子涉及粒子的位置和速度:如果我們精確地測量其位置,則其速度變得不確定,反之亦然。EPR 想知道,如果我們決定測量一對相隔遙遠的粒子中單個粒子的位置或速度,會發生什麼情況。
EPR 分析的例子涉及兩個質量相同的粒子在一維空間中運動。讓我們稱這些粒子為 R 和 J,因為它們是我們想象羅密歐和朱麗葉測量的粒子。我們可以以這樣一種方式製備它們,使它們的質心具有明確的位置,我們將其稱為xcm,等於 xR(R 的位置)加上 xJ(J 的位置)。我們可以要求質心等於零——換句話說,我們可以說這兩個粒子始終與原點等距。我們還可以使粒子的相對速度 vrel,等於 R 的速度 (vR) 減去 J 的速度 (vJ),取一個精確值;例如,vrel 等於某個我們可以稱為 v0 的數字。換句話說,兩個速度之間的差異必須保持不變。我們在這裡精確地指定了一個位置和一個速度,但不是針對同一個物體,因此我們沒有違反海森堡不確定性原理。如果我們有兩個不同的粒子,沒有什麼可以阻止我們知道第一個粒子的位置和第二個粒子的速度。同樣,一旦我們固定了質心的位置,我們就無法說出質心的速度,但我們可以自由地固定相對速度。
在這裡,我們得到了最令人驚奇的部分,以及使量子糾纏看起來如此奇怪的事情。假設我們的粒子彼此遠離,並且兩位遙遠的觀察者,羅密歐和朱麗葉,決定測量粒子的位置。現在,由於粒子是如何製備的,如果朱麗葉確定了 xJ 的任何特定值,那麼羅密歐會發現他的粒子的位置是朱麗葉的粒子的位置的負數 (xR = −xJ)。請注意,朱麗葉的結果是隨機的:她的粒子的位置會因測量而異。然而,羅密歐的結果完全由朱麗葉的結果決定。現在假設他們都測量自己粒子的速度。如果朱麗葉得到 vJ 的特定結果,那麼羅密歐肯定會發現他的速度是朱麗葉的速度加上相對速度 (vR = vJ + v0)。同樣,羅密歐的結果完全由朱麗葉的結果決定。當然,羅密歐和朱麗葉可以自由選擇他們將要測量的變數。特別是,如果朱麗葉測量位置,而羅密歐測量速度,他們的結果將是隨機的,並且不會顯示任何相關性。
奇怪的是,即使羅密歐對他粒子位置和速度的測量受到海森堡不確定性原理的約束,但如果朱麗葉決定測量她的粒子的位置,那麼一旦羅密歐知道朱麗葉的測量結果,他的粒子將具有完全確定的位置。速度也將發生同樣的情況。看起來好像當朱麗葉測量位置時,羅密歐的粒子立即“知道”它必須具有明確的位置和不確定的速度,而如果朱麗葉測量速度,情況則相反。乍一看,這種情況似乎允許瞬時傳輸資訊:朱麗葉測量位置,然後羅密歐看到他的粒子具有確定的位置,從而推斷出朱麗葉測量了位置。然而,羅密歐將無法在不知道朱麗葉測量的位置的實際值的情況下意識到他的粒子具有確定的位置。因此,事實上,由量子糾纏引起的相關性不能用於傳送速度快於光速的訊號。
儘管已透過實驗證實,但糾纏可能仍然只是一種量子系統的深奧特性。然而,在過去的二十年半中,這些量子相關性已導致密碼學和量子計算等領域的許多實際應用和突破。
等價性
我們這兩種非常不同、奇異的現象——蟲洞和糾纏——如何相關?進一步觀察黑洞為答案指明瞭方向。已故的斯蒂芬·霍金在 1974 年證明,量子效應將導致黑洞以熱物體輻射的方式發射輻射——證明傳統的“沒有任何東西可以逃脫黑洞”的說法過於簡單。黑洞輻射的事實意味著它們具有溫度——一個具有重要影響的概念。
自 19 世紀以來,物理學家們就知道溫度源於系統微觀組成部分的運動。例如,在氣體中,溫度來自分子的擾動。因此,如果黑洞具有溫度,人們可以預期它們也具有某種微觀組成部分,這些微觀組成部分共同能夠採用各種可能的配置,或所謂的微觀狀態。我們還認為,至少從外部來看,黑洞應該表現得像量子系統;也就是說,它們應該受到所有量子力學定律的約束。總之,當我們從外部觀察黑洞時,我們應該找到一個可以具有許多微觀狀態的系統,並且它處於任何這些配置中的機率對於所有微觀狀態基本上是相等的。
由於黑洞從外部看起來像普通的量子系統,因此沒有什麼可以阻止我們考慮一對糾纏的黑洞。想象一下一對非常遙遠的黑洞。每個黑洞都有大量的可能微觀量子態。現在想象一對糾纏的黑洞,其中第一個黑洞中的每個量子態都與第二個黑洞的相應量子態相關聯。特別是,如果我們測量第一個黑洞的某個狀態,則另一個黑洞必須處於完全相同的狀態。
有趣的是,基於受弦理論(一種量子引力理論的方法)啟發的某些考慮,我們可以論證,一對微觀狀態以這種方式糾纏的黑洞(即,在所謂的 EPR 糾纏態中)將產生一個時空,其中蟲洞(ER 橋)連線兩個黑洞的內部。換句話說,量子糾纏在兩個黑洞之間建立了幾何連線。這個結果令人驚訝,因為我們認為糾纏涉及沒有物理連線的相關性。但在這種情況下,兩個遙遠的黑洞透過它們的內部物理連線,並透過蟲洞拉近距離。
斯坦福大學的倫納德·薩斯坎德和我將蟲洞和糾纏的等價性稱為“ER = EPR”,因為它將愛因斯坦及其同事在 1935 年撰寫的兩篇文章聯絡起來。從 EPR 的角度來看,每個黑洞視界附近的觀測結果是相關的,因為黑洞處於量子糾纏狀態。從 ER 的角度來看,觀測結果是相關的,因為這兩個系統透過蟲洞連線。
現在,回到我們的羅密歐和朱麗葉科幻故事,我們可以看到戀人應該做什麼來形成一對糾纏的黑洞以產生蟲洞。首先,他們需要建立許多糾纏粒子對,類似於前面討論的那些,羅密歐擁有每對糾纏粒子對中的一個成員,朱麗葉擁有另一個成員。然後,他們需要構建非常複雜的量子計算機,這些計算機將操縱他們各自的量子粒子,並以受控方式將它們組合起來,以建立一對糾纏的黑洞。在實踐中實現這樣的壯舉將非常困難,但根據物理定律,這似乎是可能的。此外,我們確實說過羅密歐和朱麗葉非常聰明!
普遍原理?
引導我們得出這些想法的理念是由許多研究人員多年來開發的,最早可以追溯到 1976 年,當時在阿爾伯塔大學的維爾納·以色列撰寫的一篇文章。2006 年,Ryu Shinsei 和 Tadashi Takayanagi(當時都在加州大學聖巴巴拉分校)也發表了關於糾纏和時空幾何之間聯絡的有趣工作。薩斯坎德和我受到了艾哈邁德·阿爾姆海里、唐納德·馬洛夫、已故的約瑟夫·波爾欽斯基和詹姆斯·蘇利(當時都在加州大學聖巴巴拉分校)於 2012 年發表的研究的啟發。他們發現了一個與糾纏黑洞內部性質相關的悖論。ER = EPR 的思想,即內部是連線黑洞和另一個系統的蟲洞的一部分,緩解了這個悖論的某些方面。
儘管我們使用黑洞確定了蟲洞和糾纏態之間的聯絡,但人們很想推測這種聯絡更普遍——即無論何時我們有糾纏,我們都有一種幾何連線。即使在最簡單的情況下,當我們只有兩個糾纏粒子時,這種期望也應該成立。然而,在這種情況下,空間連線可能涉及微小的量子結構,這些結構不會遵循我們通常的幾何概念。我們仍然不知道如何描述這些微觀幾何形狀,但這些結構的糾纏可能會以某種方式產生時空本身。就好像糾纏可以被視為連線兩個系統的線索。當糾纏量變得更大時,我們有很多線索,這些線索可以編織在一起形成時空的結構。在這樣的圖景中,愛因斯坦的相對論方程正在支配這些線索的連線和重新連線;量子力學不僅僅是引力的附加物——它是時空構造的本質。
目前,這種圖景仍然是瘋狂的猜測,但一些線索指向了它,我們許多物理學家正在追求它的含義。我們相信,看似無關的糾纏和蟲洞現象實際上可能是等價的,並且這種等價性為開發量子時空的描述——以及期待已久的廣義相對論和量子力學的統一——提供了重要的線索。
