所有籃球迷都知道手感火熱:將球傳給處於得分連勝的隊友,因為她或他投進下一個球的機會比平時更高。這個備受推崇的原則在 1985 年被托馬斯·吉洛維奇、羅伯特·瓦隆和阿莫斯·特沃斯基推翻。他們對費城 76 人隊的投籃命中率資料、波士頓凱爾特人隊的罰球資料以及康奈爾大學校隊和少年隊籃球運動員進行的 100 球/人受控實驗的統計研究似乎證明,這種得分連勝並非不同尋常。儘管球迷認為他們的球員手感火熱,但連勝可以用純粹的運氣來解釋。
這個改變遊戲規則的訊息在職業體育界反響平平。當手感火熱研究釋出時,波士頓凱爾特人隊總裁雷德·奧爾巴赫就特沃斯基發表了他的看法:“這傢伙是誰?所以,他做了一項研究。我一點也不在乎。”
然而,學術界似乎對這一發現很著迷。1985 年的研究引發了大量的學術文獻,而手感火熱問題推動了對專業人士的直覺與冷冰冰的科學事實之間衝突的調查。在他的暢銷書《撤銷專案》中,邁克爾·劉易斯講述了阿莫斯·特沃斯基和他的終身合作者、諾貝爾獎獲得者丹尼爾·卡尼曼的故事。他們的研究促使了行為經濟學的研究,並改變了我們對人類決策缺陷的理解。劉易斯寫道:“特沃斯基清楚地知道人們是如何誤解隨機性的……人們有不可思議的能力在根本不存在的模式中看到意義。”
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
在他們的職業生涯早期,阿莫斯·特沃斯基和丹尼爾·卡尼曼考慮了人類根據少量觀察得出結論的傾向,他們稱之為“小數定律”。這是對大數定律的一種戲謔的暗示,大數定律提供了關於何時可以從大型資料集得出準確推論的指導。關於如何從小資料集得出推論沒有通用的規則,而且可能很難注意到存在問題。
手感火熱的基本統計公式
在統計實驗中,有很多方法可以表示“手感火熱”的概念。在本研究和原始研究中一樣,手感火熱是指在連續命中投籃的情況下,投籃命中的機率異常高。
這個公式忽略了比賽的一些細節。有些投籃比其他投籃更難,而且對方的防守動作可能會使表現出色的球員處於不利的位置。儘管如此,在嘗試增加真實感之前,先看看這個簡單實驗的結果是很有趣的。
對於“異常高”這個術語,也有很多種定義方法。我們再次遵循原始的手感火熱研究,該研究依賴於條件機率的差異:在連續命中投籃的情況下投籃命中的機率減去在同樣長的連續不中投籃的情況下投籃命中的機率。如果觀察到的差異相對於與相同長度和相同命中次數的隨機字串對應的典型差異較大,則該觀察結果對應於手感火熱。
原始手感火熱研究中的“小數定律”錯誤及更正
2015 年,統計學家喬什·米勒和亞當·桑朱爾喬記錄了原始手感火熱研究中的一個錯誤。該錯誤與小數定律有關。為了理解這個錯誤,請考慮克萊·湯普森在 2016 年 12 月 23 日對陣底特律活塞隊的比賽中的投籃記錄。該記錄用一串 1(命中)和 0(不中)表示
1110100110000011:
湯普森在這場比賽中出手 16 次,碰巧他正好投中了一半。我們可以看看我們關於這個字串上手感火熱的統計公式。首先,我們計算在之前兩次命中的情況下命中的經驗機率。有四次連續兩次命中的情況,用字串 11 表示。我們知道前三次 11 的情況之後發生了什麼:湯普森第一次命中,第二次和第三次不中。但在第四次 11 的情況之後什麼也沒有發生,因為比賽在他可以再次投籃之前就結束了。我們將最後的 11 稱為未實現的條件集,它使手感火熱研究中使用的條件機率的估計複雜化。
也許我們能說的最好的是,在正在考慮的比賽中,我們觀察到湯普森在連續兩次命中後三分之一的時間得分。在另一個方向,鑑於湯普森連續兩次不中,他五分之二的時間得分。第二個計算更直接,因為沒有未實現的條件集。兩個條件機率的差是 1/3 - 2/5 = -1/15。
這個差異 -1/15;異常高嗎?也許對於這個一半命中一半不中的字串,有一個自然的基準來衡量“異常”。根據資料,也許可以合理地假設在兩次命中後投籃命中的機率與在兩次不中後投籃命中的機率相同:50%。與此基準相比,條件機率的平均差為 0,這使得 -1/15 看起來並不異常高。這個基準與原始的手感火熱研究一致。
然而——這就是小數定律發揮作用的地方——50-50 基準是錯誤的選擇。如果我們處理的是無限字串,那麼這將是正確的,但比賽不會無限期地進行下去。在實踐中,我們處理的是有限字串。許多字串都有未實現的條件集,有些字串根本沒有條件集,因此自然基準需要小樣本調整。在長度為 16 的字串中,一半是 1,一半是 0,在兩次命中後投籃命中的機率小於在兩次不中後投籃命中的機率:反轉比延續更可能發生。這就是米勒和桑朱爾喬的觀察結果,它與賭徒謬誤一致,即認為命運的逆轉是“應該”發生的。考慮到這種現象,條件機率的預期差值小於零。這為一項研究留下了可能性,該研究使用不正確的 50-50 零假設,在正確指定的零分佈會導致拒絕的情況下,未能拒絕零假設。
原始研究中沒有手感火熱的結論是基於觀察到的資料與錯誤的基準之間的統計上不顯著的差異。當對康奈爾大學球員進行的 100 球/人受控實驗應用所需的調整時,米勒和桑朱爾喬報告說,在幾個案例中,沒有手感火熱的發現被推翻了。
尋找勇士隊的手感火熱
正如米勒和桑朱爾喬指出的那樣,觀察到的命中和不中字串的排列檢驗會自動實現小樣本校正 [2,第 3.1 節]。在該檢驗中,特定零和一字串的屬性與字串條目的隨機重排中的相同屬性進行比較。這允許對屬性的稀有性進行定量評估。
在這裡,我們使用排列檢驗來確定庫裡、湯普森和杜蘭特在哪些比賽中手感火熱,根據原始研究中的公式。我們還逐節調查了勇士隊的手感火熱程度。
資料
對於庫裡、湯普森和杜蘭特,我們編制了一個由 1 和 0 組成的字串,表示他們在 2016-2017 賽季常規賽和季後賽中每場比賽的命中和不中情況。庫裡打了 96 場比賽,湯普森打了 95 場,杜蘭特打了 77 場。我們還編制了勇士隊逐節的命中和不中字串,在整個賽季中,共得出 396 = 99 x 4 節。
實驗設計和檢驗統計量
觀察值 X 是庫裡、湯普森或杜蘭特一場比賽的命中和不中字串,或者是勇士隊一節比賽的命中和不中字串。該字串包括投籃和罰球。我們使用排列檢驗來確定觀察值是否顯示出手感火熱的證據。
對於觀察到的字串,我們計算了檢驗統計量 tk;給定 k 次先前命中的條件下命中的條件分數減去給定 k 次先前不中的條件下命中的條件分數,其中 k 等於 1、2 或 3。然後,我們對錶示投籃模式的 0 和 1 字串進行 10,000 次排列,並計算每個排列的 tk。
從數學上講,長度為 L 的字串 X 上的檢驗統計量 tk 定義如下
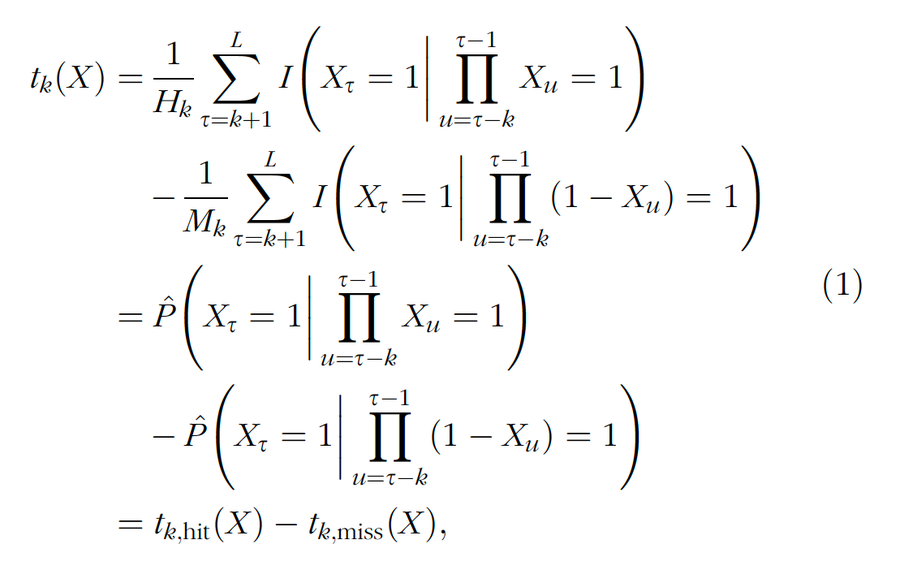
其中 Hk 和 Mk 是由投籃緊隨其後的 k 次命中和 k 次不中的子字串的數量,Xτ 是 X 的第 τ 個條目,而 P̂ 是經驗機率。值 k 是條件集的深度。
超過觀察到的檢驗統計量的排列檢驗統計量的分數是其 p 值。在實踐中,許多排列字串上的檢驗統計量的值與觀察到的投籃模式上的檢驗統計量的值相同。因此,在如何定義 p 值方面存在一定的自由度。從數學上講,這種自由度對應於以下兩者之間的選擇
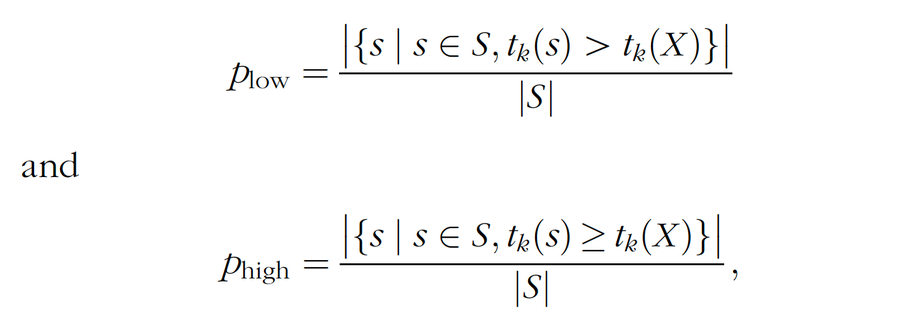
其中 S 是排列字串的集合。我們使用 Plow;這使得儘可能容易地拒絕“沒有手感火熱”的零假設。較小的 p 值對應於手感火熱的更強證據。
結果
描述投籃次數和命中頻率的統計資料顯示在表 1 中。
下面呈現的結果主要關於 t2;它沒有顯示出手感火熱的證據。t3 的結果在質量上相似,儘管 t1 中有手感火熱的跡象:在 96 場比賽中,斯蒂芬·庫裡的投籃字串在條件集深度為 1 的情況下,在 5% 的水平上顯著。同樣,勇士隊作為一個團隊在使用 t1 的 396 節比賽中,有 35 節比賽顯示出手感火熱的跡象:但是,我們認為這些結果構成了支援手感火熱的微弱證據,因為在不太寬鬆的測試條件下,明顯的效應消失了。也就是說,當我們使用更傳統的 p 值計算方法 Phigh(如上一節所述)時,庫裡的顯著比賽場次降至 96 場中的 7 場,勇士隊的顯著節數降至 396 節中的 26 節。此外,當我們刪除罰球資料時(球員的罰球命中率往往高於正常比賽期間),庫裡的表現僅在 5 場比賽中具有統計學意義,而勇士隊僅在 21 節比賽中具有統計學意義。有關更多詳細資訊,請參見附錄。
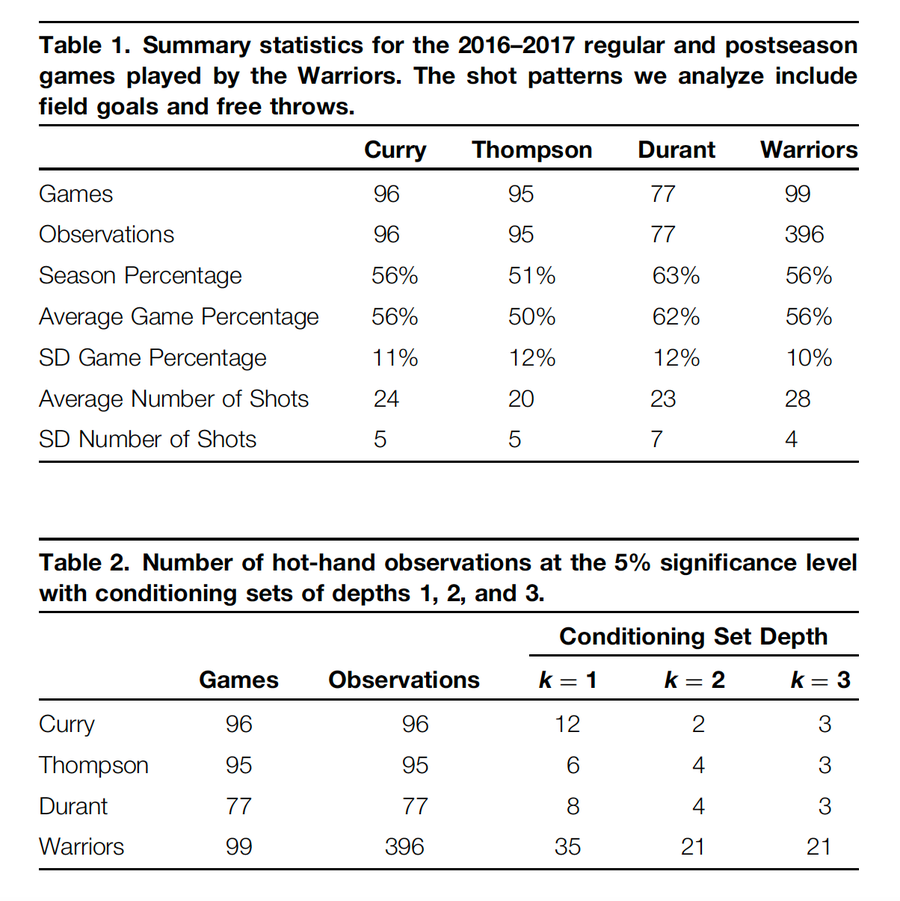
表 2 顯示了在 2016-2017 賽季庫裡、湯普森和杜蘭特進行的比賽以及勇士隊進行的節數中,深度為 1、2 和 3 的條件集在 5% 水平上顯著的觀察次數。在 5% 水平上顯著的觀察結果很少。
除了原始手感火熱研究中的 tk 統計量外,我們還考慮了許多其他可能指示手感火熱的統計量。我們只查看了 tk 的左和項;tk,hit:在這種情況下,我們測試了手感火熱的更簡單的定義:如果球員在連續成功投籃後投籃命中的機會更高,則該球員手感火熱。“機會更高”的概念在此處的定義方式與上述測試中相同。
對於我們的兩個檢驗統計量,我們還考慮了兩個額外的非引數檢驗。首先,我們沒有排列給定比賽的投籃字串,而是透過模擬 10,000 個新的二元字串來估計檢驗統計量的分佈,方法是模擬 n 次伯努利 (p) 試驗,其中 p 是該球員在該比賽中的投籃命中率,n 是該球員的投籃次數。在第二個測試中,我們再次模擬了 n 次伯努利試驗;但是,我們讓 p 等於被測試比賽開始時球員的賽季投籃命中率。這些替代公式得出了相同的結論:很少或沒有手感火熱的證據。
一個例子
2016 年 12 月 5 日,湯普森對陣印第安納步行者隊得到 60 分。他 44 次投籃命中 31 次,他在該場比賽中的記錄如下所示
X60: 11011110010111111001110111101110111101010101
這是否表明手感火熱?有 19 次字串 11 的例項,其中 12 次後面跟著命中。有兩次字串 00 的例項,它們後面都跟著命中。因此 t2 = 12/19 - 1 = -7/19。
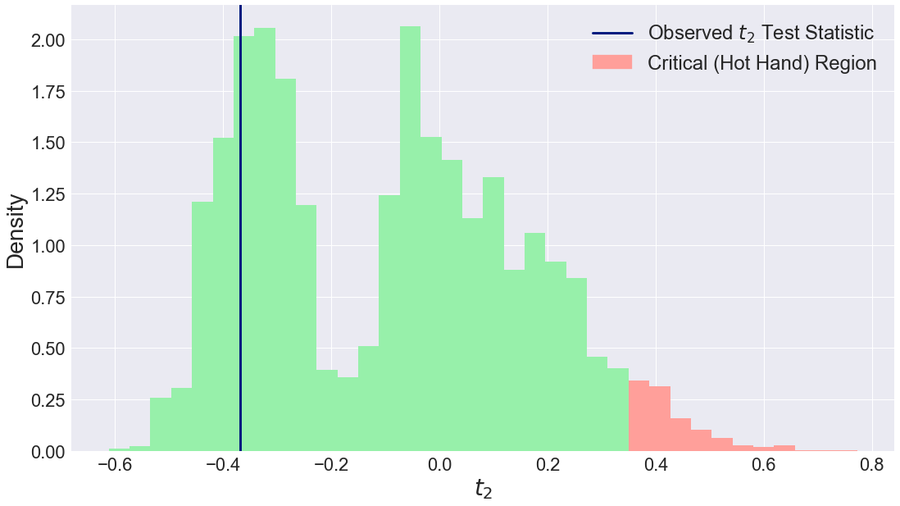
圖 1. 湯普森 2016 年 12 月 5 日對陣印第安納步行者隊的 60 分比賽的 t2 統計量。綠色區域代表零假設,對應於觀察到的字串的 10,000 次排列的 t2 值的直方圖。藍線標記觀察到的字串的 t2 值,紅色臨界區域對應於 t2 值最高的 5%:手感火熱。圖片來源:阿隆·達克斯
圖 1 顯示了基於湯普森 X60 字串的 10,000 次排列的 t2 統計量的直方圖。綠色區域代表零分佈,對應於觀察到的字串的 10,000 次排列的 t2 值的直方圖。在附錄中,我們探討了零假設的雙峰性及其形狀的其他不規則性。藍線標記觀察到的字串的 t2 值,紅色臨界區域對應於 t2 值最高的 5%:手感火熱。
這個觀察結果因其長度而非常特殊,而且因其命中百分比 31/44 ≈ 70% 而非常特殊:但條件機率的差異 -7/19;的 p 值為 0.84,這根本不特殊。
最終觀察
儘管我們像統計學家一樣檢查了“水花兄弟”斯蒂芬·庫裡和克萊·湯普森以及 2016-2017 賽季常規賽的射擊記錄以及 2017 年總決賽 MVP 凱文·杜蘭特的射擊記錄,但我們希望指出,觀看這些球員在球場上的比賽是一種神奇的體驗。當他們進入狀態時,他們似乎就是手感火熱的化身。然而,我們的統計研究講述了一個不同的故事。它表明,在 2016-2017 賽季的大部分常規賽比賽中,他們都不是連勝射手。因此,在調整了小樣本效應後,我們的結論與最初的結論相似,後者沒有考慮到小樣本效應。
當然,這並不是故事的結局。手感火熱長期以來一直讓體育專業人士和研究人員著迷,我們對於思考這個問題的正確方法尚未達成共識。然而,每項實證手感火熱研究都將依賴於有限的資料集,因此小樣本效應勢必會在對結果的任何正確解釋中發揮作用。
阿莫斯·特沃斯基於 1996 年去世,享年 59 歲,距離他本應與丹尼爾·卡尼曼分享的諾貝爾獎頒發還有五年,距離發現他的手感火熱研究中的錯誤還有近二十年。如果他今天與我們同在,這位了不起的研究人員和狂熱的籃球迷無疑會對他的錯誤的糾正感到高興,並且他肯定會觀看引人入勝的金州勇士隊的比賽。
附錄:解構 t2 的零假設
在本附錄中,我們將更仔細地研究圖 1 中描繪的湯普森對陣印第安納步行者隊的 60 分比賽的零假設。公式 (1) 將 t2 表示為機率差
tk = tk,hit - tk,miss。
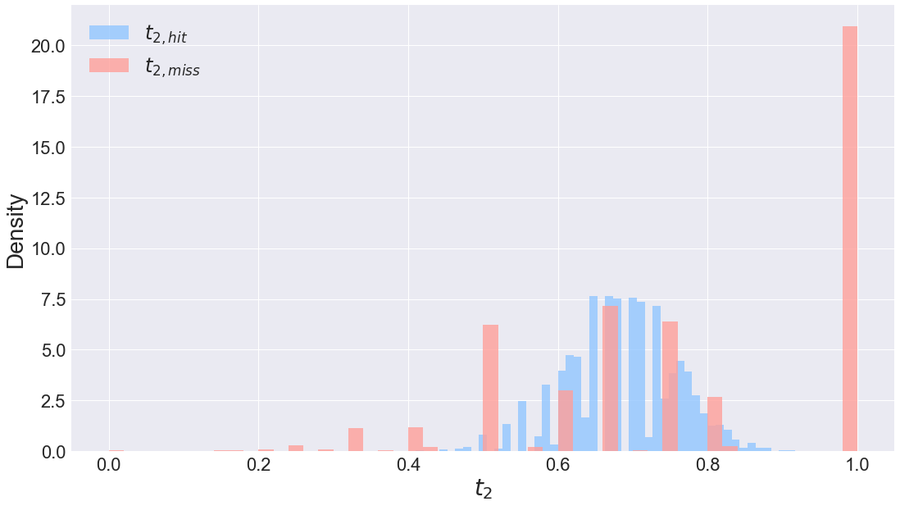
圖 2. 湯普森 2016 年 12 月 5 日對陣印第安納步行者隊的 60 分比賽的 t2,hit 和 t2,miss 直方圖。圖片來源:阿隆·達克斯
在圖 2 中,我們顯示了 tk,hit 和 tk,miss 的直方圖。這些直方圖的形狀完全由字串的長度 44 和命中百分比 31/44 ≈ 70% 決定:t2,miss 在 1 處的峰值出現是因為不中投籃相對罕見:在許多長度為 44 且命中次數為 31 的字串中,所有連續的後面跟著任何東西的不中對都跟著命中。
對於較長的字串和 50% 左右的命中機率,t2 及其分量的分佈往往是單峰且對稱的。但是對於相對較小的字串,例如,頂級職業籃球運動員在一場比賽中的投籃次數,表示 t2 及其分量的零假設的直方圖可能是不規則的。因此,本文中使用的型別的有限樣本方法可能優於漸近結果。
僅限投籃
本文分析的字串包括投籃和罰球。然而,當我們分析投籃字串時,我們的結論是相同的。
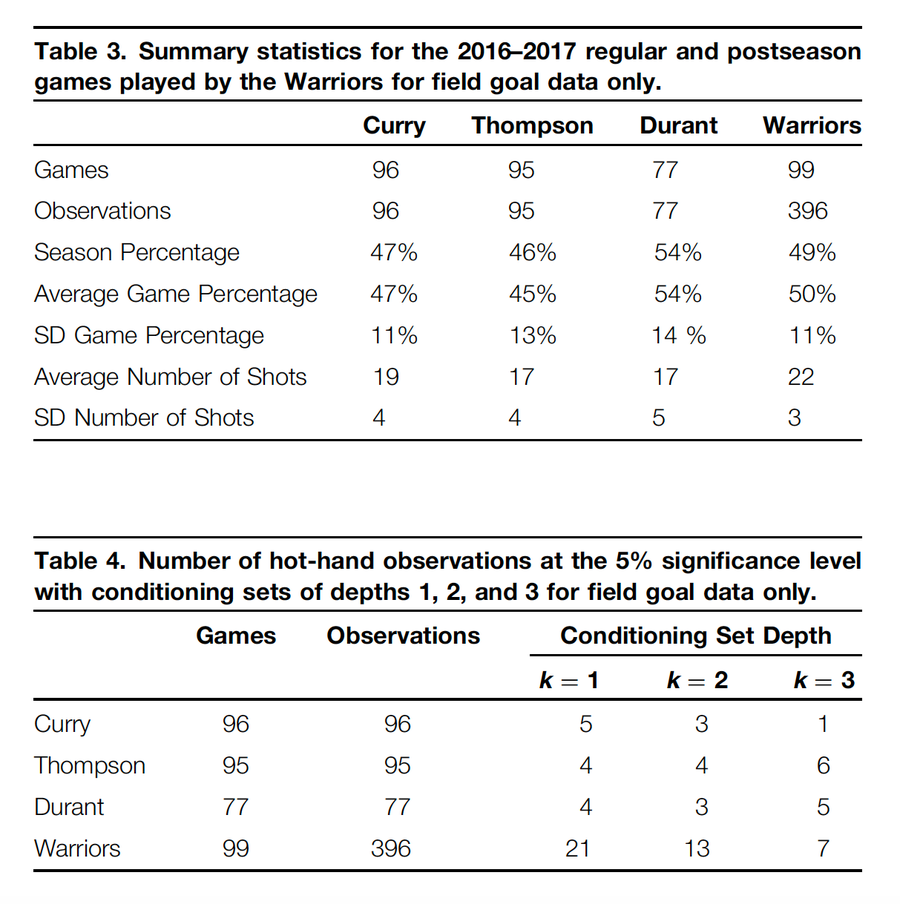
描述嘗試投籃和命中頻率的統計資料顯示在表 3 中。表 4 顯示了在 2016-2017 賽季庫裡、湯普森和杜蘭特進行的比賽以及勇士隊進行的節數中,深度為 1、2 和 3 的條件集在 5% 水平上顯著的觀察次數。在 5% 水平上顯著的觀察結果很少。
經《數學情報家》許可轉載。
