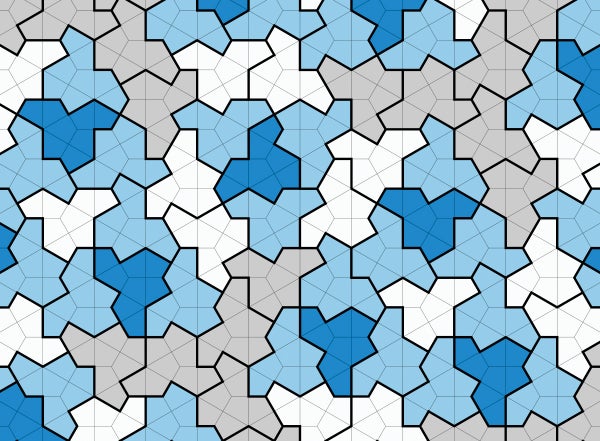
來自英國約克郡的數學愛好者大衛·史密斯發現了一種 13 邊形,這個形狀幾十年來一直讓數學家們捉摸不透。這種崎嶇不平、類似帽子的形狀被稱為“愛因斯坦”,源自德語中的“一塊石頭”。如果您使用愛因斯坦形狀的瓷磚來鋪設浴室地板——或任何平面,即使是無限大的平面——它們將完美地拼合在一起,但永遠不會形成重複的圖案。幾十年來,數學家們一直在尋找像這樣的瓷磚形狀,它們只能形成非重複排列,稱為非週期性平鋪。他們從多組不同的瓷磚開始:第一組於 1964 年被發現,需要 20,426 塊不同的瓷磚,後來簡化為 103 塊。到 1974 年,數學家羅傑·彭羅斯發現了兩種瓷磚形狀,當它們組合成馬賽克時,永遠不會形成重複的圖案。
但是,是否有可能僅用一種形狀的瓷磚——假設的愛因斯坦瓷磚——形成非週期性平鋪?多麗絲·沙茨施耐德是一位退休數學家,隸屬於莫拉維亞大學,在鑲嵌方面擁有專業知識,她一直對真正愛因斯坦瓷磚被發現的可能性持懷疑態度。“這就是為什麼不僅發現了它,而且它還是如此簡單的瓷磚,這令人如此震驚,”她說。“對我來說,這是一個完全的異常現象。”史密斯於 2022 年 11 月發現的瓷磚,當時他正在使用名為 PolyForm Puzzle Solver 的軟體試驗不同的形狀,其優雅性令人震驚。它由直角風箏形組成,與許多數學家預測的粗糙、複雜的形狀截然不同。
史密斯給安大略省滑鐵盧大學的計算機科學家克雷格·卡普蘭傳送了電子郵件,卡普蘭認識到了這種形狀的潛力。儘管它建立的馬賽克似乎沒有重複的圖案,但兩人需要從數學上證明它永遠不會——即使馬賽克是無限大的。他們請來了軟體開發人員約瑟夫·塞繆爾·邁爾斯和阿肯色大學數學家查伊姆·古德曼-施特勞斯,他們過去都曾從事平鋪和組合數學方面的工作。
支援科學新聞報道
如果您喜歡這篇文章,請考慮支援我們屢獲殊榮的新聞報道,方式是 訂閱。透過購買訂閱,您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
研究人員使用了兩種方法來證明他們手中擁有真正的愛因斯坦瓷磚。首先,他們表明,當帽子狀瓷磚排列在一起時,會形成四種特定的形狀。新增更多瓷磚會形成這些相同形狀的更大版本,或“超瓷磚”;新增的瓷磚越多,超瓷磚就越大。數學家已經證明,這種分層結構意味著平鋪無法分割成重複的部分,因此必須是非週期性的。對於第二個證明,該團隊發明了一種新方法,可以將帽子平鋪與更著名的稱為多邊形鑽石的形狀的非週期性平鋪進行比較。在這個過程中,該團隊還表明,人們可以透過調整某些邊的長度來製作無限數量的類似愛因斯坦瓷磚。
即使有了這些證明,數學家們還沒有制定出更廣泛的理論來解釋為什麼這種簡單的帽子形狀如此特別。“這仍然非常神秘,”新澤西州普林斯頓高階研究所的數學家雷切爾·格林菲爾德說。可能還有更多類別的愛因斯坦瓷磚有待發現,但幾何帽子並沒有透露任何線索,隸屬於史密斯學院的退休數學家馬喬裡·塞內沙爾說:“這些東西是你偶然發現的。”
編者注:此故事的早期版本曾在網上以標題 “新發現的數學“愛因斯坦”形狀創造了一種永不重複的圖案”發表。