關鍵概念
圓
圓周長
直徑
數學公式
圓周率
導言
數學家們對數學關係的發現感到興奮。他們用數字、公式和方程式來看待周圍的世界。數學也很有趣且實用。當計算您需要存多久的零用錢才能買一個新遊戲時,它會派上用場。您可以使用數學來將食譜加倍或三倍,或者計算您最晚可以幾點離開家,並且仍然可以準時到達學校。
您還可以使用它來預測事物的大小——在紙上或在現實世界中。在這個科學活動中,您將檢查圓形物體,看看您能發現關於它們大小的哪些關係。您將探索圓的圓周長是否以某種特定的方式與其直徑相關。當您探索這種關係時,您可能會對結果的有用性感到驚訝;也許它會激勵您存錢買一輛更大的腳踏車!
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和想法的具有影響力的故事的未來。
背景
您知道人們研究數學已經有數千年了嗎?我們今天使用的許多數學術語都源於希臘語和拉丁語,揭示了一些研究這些問題的古代學者的起源。例如,單詞“circumference”(圓周長)來自拉丁語單詞 circum(意思是“周圍”)和 ferre(意思是“攜帶”)。它可以指圓的邊界線,也可以指該線的長度。單詞“diameter”(直徑)源於希臘語單詞 dia(“橫穿”)和 metron(“測量”)。它指的是一條直線,該直線從圓周上的一個點開始,穿過圓心,並在圓的另一側結束。它也可以指這條線的長度。數學家已經證明,直徑也是穿過圓的最長距離。
術語夠多了!是時候開始探索了。
材料
至少四個不同大小的圓形物體(例如,您可以使用大硬幣、圓形容器蓋、大型容器蓋和腳踏車輪。)
一大卷細繩或絲帶,您可以將其剪成小塊
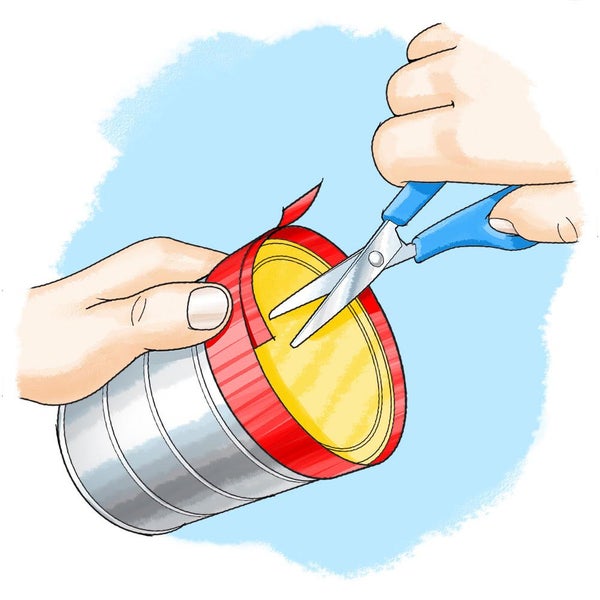
剪刀(應由成人幫助您使用。)
膠帶,例如美紋紙膠帶(可選)
準備
將您的所有物品集中在一個區域,以便於取用。
從一箇中等大小的圓開始您的探索,例如酸奶容器蓋。在接下來的幾個步驟中,您將剪下幾段細繩(或絲帶),其長度分別為該圓的圓周長和直徑。一旦您準備好這些線段,您就可以開始探索它們是否以某種特定的方式相關。您將對不同大小的圓重複此過程,以期發現您所有示例的直徑和圓周長以相同的方式相互關聯。
步驟
要建立一段長度等於第一個圓形物體的圓周長(圓的邊界線)的細繩,請用拇指將一段細繩的一端按在圓形物體邊緣上的一個點上。
將細繩繞物體正好一圈,並在纏繞的細繩與其起點相遇的地方剪斷細繩。為了使操作更輕鬆一些,您可以暫時用膠帶將細繩的開頭粘在圓形物體上,然後纏繞細繩並沿著膠帶剪斷。您能看到您的細繩的長度正好是您的圓形物體的圓周長嗎?
要測量直徑,您需要一條直線的長度,該直線從圓周上的一個點開始,穿過圓心,並在其另一側結束。因為不容易找到圓心,所以您將使用關於圓的數學事實,該事實指出直徑也是穿過圓的最長距離。要建立一段具有穿過圓的最長長度的細繩,請用拇指將一段新的細繩(或絲帶)的一端按在中等大小的圓形物體邊緣上的一個點上。
將這段細繩拉直,橫跨圓到圓周上的另一點。現在沿著圓周移動第二個點——向左和向右。這樣做直到找到可能的最長的直線跨度細繩。當您將細繩的末端從該點移開時,跨度細繩又會變短。在細繩最長的地方剪斷,以獲得該圓的直徑的測量值。您是否觀察到您的跨度細繩穿過了圓心?
現在您擁有開始探索所需的一切。哪個距離更長——直徑還是圓周長?是長很多還是長一點?
如果您將較長的細繩對摺,它是否適合另一段細繩的長度?如果是這樣,則意味著較長的細繩是較短的細繩的兩倍長。如果您對摺較長的細繩後沒有找到合適的長度,那麼如果您將其摺疊成三份、四份或五份呢?您得到的是精確的還是近似的擬合?您將如何用“兩倍長”或“三倍長”之類的詞語來翻譯您的發現?
用不同大小的圓形物體再次嘗試該活動。您是否期望圓周長和直徑長度之間的相同關係對於不同大小的圓也有效?
重複圓周長和直徑的查詢,直到您探索了一個微小、中等、大和非常大的圓。您能找到一個對所有測試的圓都有效的關係嗎?它是精確的關係還是近似的關係?如果您找到了關係,您認為您有足夠的資料來得出您的關係對所有圓都有效的結論嗎?
額外內容:在房子周圍尋找一些圓形物體,並估計這些物體的直徑和圓周長的長度。對您來說,哪個更容易估計,直徑還是圓周長?哪個更容易用尺子測量?
額外內容:如果您找到了圓周長和直徑之間的近似關係,您如何使其更精確?提示:您可以使用尺子測量您的細繩的長度並進行一些數學運算。(例如,嘗試將圓周長除以其對應的直徑;對每個圓再次嘗試。每次您是否得到相似的數字——無論圓的大小是否相同?)
額外內容:該原理的一個實際應用是計算不同尺寸的車輪行駛的距離。為了探索地面行駛距離和車輪尺寸之間的關係,用膠帶在車輪(例如腳踏車輪)的圓周上標記一個點。將該點放在地面上,並在地面上用膠帶或粉筆標記該位置。沿直線滾動車輪,直到圓周上的同一點再次接觸地面。在地面上用膠帶或粉筆標記該位置。現在將地面上兩個標記位置之間的距離與車輪的直徑和圓周長的長度進行比較。您能找到關係嗎?對於較大或較小的車輪行駛相同距離可能需要的旋轉次數,這意味著什麼?
額外內容:既然您知道了直徑與圓周長的關係——甚至可能知道了行駛距離——您能看到這種關係可以在哪些實際方面有用嗎?
[break]
觀察和結果
如果一切順利,您應該已經發現,對於每個圓,無論圓的大小如何,圓周長都比直徑略大三倍。
如果您能夠更精確地工作,您可能會發現它不是正好三倍,而是直徑的三又七分之一。即使這樣也不精確。
數學家發現,圓的圓周長與直徑之比是一個常數,這意味著對於所有圓,無論圓的大小如何,該比率都相同。然而,他們也發現,這個比率是一個永遠無法精確確定的數字。自19世紀中期以來,這個比率一直用希臘字母 π(pi)表示,這是一個非常有趣的數字。它不僅出現在幾何學中,也出現在其他數學領域,例如機率論。它也出現在自然界中,例如在波浪的描述中——從可見的水波紋到不可見的光波和聲波。
更多探索 史前微積分:發現圓周率,來自Better Explained
用數學描述自然,來自NOVA 在圓周率日談論圓周率和餡餅,來自Science Buddies
此活動由Science Buddies合作推出