數千年來,人們一直在玩魔方——由不同的數字組成的陣列,其行、列和對角線的總和都相同。*一個簡單的 3x3 陣列,每種方式加起來都等於 15,出現在中國傳說洛書的烏龜背上,該傳說可以追溯到公元前 650 年。中東和印度的中世紀數學家研究了各種尺寸的魔方,阿爾布雷希特·丟勒在他 1514 年創作的著名版畫《憂鬱 I》中加入了一個 4x4 的魔方。今天,業餘和專業數學家繼續設計新的魔方,甚至增加額外的維度來設想 3D 魔方和 4D 魔方體。
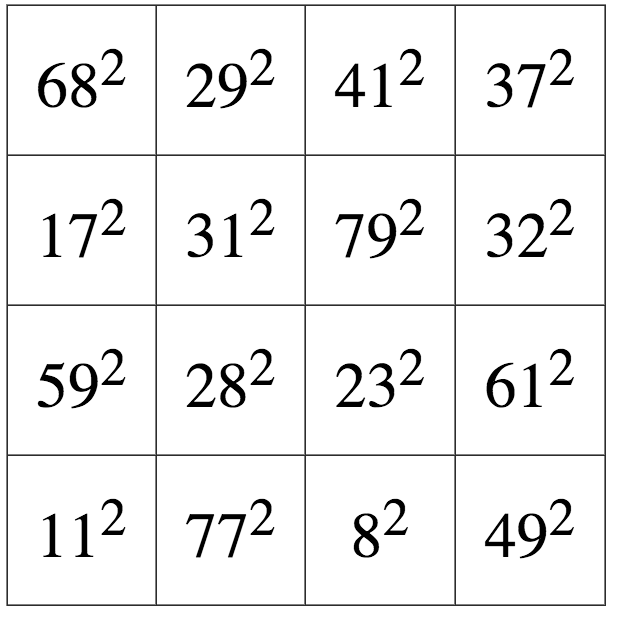
18 世紀的數學家萊昂哈德·尤拉對另一種奇異的魔方感到困惑,這種魔方完全由平方數構成。1770 年,他介紹了第一個 4x4 平方數魔方的例子(如下),以及生成其他魔方的公式。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
現在已知許多 4x4 平方數魔方,大約 10 年前,克里斯蒂安·博耶報告了 5x5、6x6 和 7x7 平方數魔方的首批示例。然而,迄今為止,沒有人發現 3x3 平方數魔方,也沒有人證明這是不可能的。
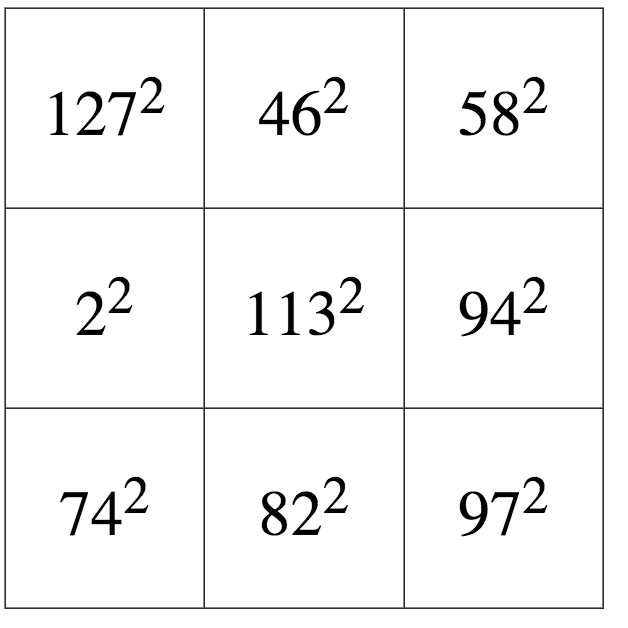
1996 年,為《大眾科學》撰寫“數學遊戲”專欄約 25 年的馬丁·加德納向任何能夠設計出解決方案的人提供了 100 美元的獎金。一年後,魔方專家李·薩洛斯描述了一個差一點成功的例子(見下文),只有一個對角線的總和不同(從左上到右下得到 38,307,而不是所有其他方向的總和 21,609)。
到目前為止,這是任何人所能達到的最接近的程度。您會成為第一個解決這兩個問題的人嗎?在下面釋出您自己設計的解決方案和魔方。如果收到足夠有趣的提交內容,其中一些將會在未來的部落格文章中在 www.ScientificAmerican.com 上展示。*澄清(2014 年 10 月 20 日):此句子在釋出後經過編輯。原文沒有明確指出每個魔方中的數字彼此不同。
您需要啟用 JavaScript 才能使用小部件。