哪個開關? 腦筋急轉彎
一棟建築的底層有三個開/關開關。只有一個開關控制三樓的單個燈泡。其他兩個開關未連線到任何東西。隨意設定開關的開/關順序。然後去三樓檢視燈泡。不用離開三樓,你能弄清楚哪個開關是真的嗎?你只有一次機會。
[答案:] 開啟前兩個開關,關閉第三個開關。等待 10 分鐘,然後關閉第一個開關,去三樓。如果燈泡熄滅但發熱,則第一個開關是控制它的開關;如果燈泡亮著,則第二個開關是真的;如果燈泡熄滅且發冷,則第三個開關是真的。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於發現和塑造我們當今世界的想法的有影響力的故事。
[中斷]

密碼算術
在這些問題中,每個字母對應一個數字。例如,你能算出每個字母代表哪個數字才能使右側的算式成立嗎?
[答案:] S = 3 E = 0 V = 8 N = 7 F = 2 O = 1 R = 5 T = 6 Y = 4
要開始解決這個問題,請注意 7 乘以 N 等於某個以 9 結尾的數字,因此 N 必須是 7。從這個資訊中,您就知道 7E + 4 等於某個以 Y 為個位數的數字,然後可以開始嘗試。例如,E 不能是 1,因為那樣 Y 也會是 1,如果 E 是 2,那麼 V 就不能是 1。以這種方式繼續推理最終會得出上面的答案。
[中斷]
令人困惑的多面體
你能想象一個由正方形底面和四個等邊三角形組成的實心金字塔,以及一個具有四個面與金字塔三角形面相同的實心四面體嗎?現在將金字塔的一個三角形面粘合到四面體上的一個三角形上。由此產生的多面體有多少個面?不是七個!
[答案:] 在組合實體中,有兩個位置兩個三角形面——每個組成實體各一個——完美對齊,形成一個面。因此,新多面體的面總數僅為 5 個(一個正方形、兩個三角形和兩個菱形)。
[中斷]
等角多邊形證明
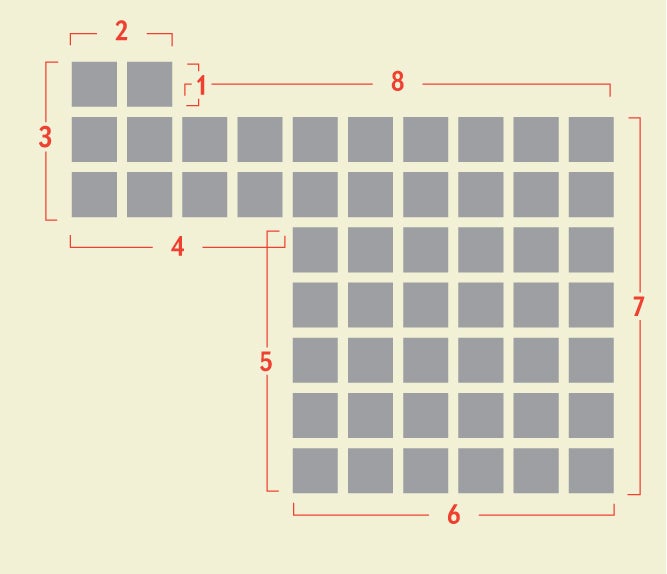
考慮一類稱為序列等角多邊形的Polygon。所有相鄰邊都以 90 度角相交,並且邊長遞增:1、2、3、4,依此類推。最簡單的等角多邊形,邊長為 1-8,如右圖所示。這是已知唯一可以平鋪平面的序列等角多邊形。但是還有更多的等角多邊形。你能證明它們的邊數必須始終是 8 的倍數嗎?
[答案:] 任務是證明對於任何 90 度序列等角多邊形,邊數必須是 8 的倍數。
將等角多邊形想象成一條閉合路徑,在標準方格紙的格線上繪製。假設路徑從向東的單位移動開始;向東或向北移動為正,向南或向西移動為負。您可以透過在移動序列中每個數字前面加上加號或減號來描述這樣的路徑,以指示移動方向。例如,謎題樣本中顯示的 8 邊等角多邊形具有以下公式: +1 + 2 – 3 – 4 – 5 – 6 + 7 + 8。
因為路徑必須閉合才能形成等角多邊形,所以所有水平移動(奇數)的總和必須為零,並且所有數字的總和也為零。同樣因為路徑是閉合的,我們知道邊數必須是 4 的倍數,比如 4k。(很容易看出它永遠不可能是 4 本身——馬丁·加德納開玩笑說這是一個“四邊形結論”。)那麼南北移動是偶數長度的移動,2、4、… 4k。因此,南北總距離為 2(1 + 2 + … + 2k) = 2k(2k + 1)。其中一半,k(2k + 1),必須向北,一半向南。
但是如果 k 是奇數,則此距離是奇數,並且不能是偶數長度移動的總和。例如,考慮一個 12 邊的等角多邊形(在這種情況下,k = 3)。其公式中的偶數(2、4、6、8、10、12)加起來為 42。如果該公式描述了一條閉合路徑,則該序列中正數的總和必須等於 42/2 = 21。但是,沒有一組偶數可以加起來為 21。因此,無法構造公式來描述 12 邊的等角多邊形。
這個例子表明,如果邊數是 4 的倍數但不是 8 的倍數(k 為奇數的所有情況,例如 12,路徑的最後一段是垂直的,無法返回到穿過路徑原點的水平格線:向北的正線段之和不能等於向南的負線段的絕對值之和。路徑終點將始終在零水平線上方或下方偶數個單位處結束。
[中斷]
不受攻擊的皇后
國際象棋棋子的屬性在許多挑戰中發揮作用,包括在一組關於不受攻擊的皇后的問題中。想象一下在一個 5 × 5 的棋盤上有三個白皇后和五個黑皇后。你能安排它們,使一種顏色的皇后不能攻擊另一種顏色的皇后嗎?只有一個解決方案,不包括反射和旋轉。
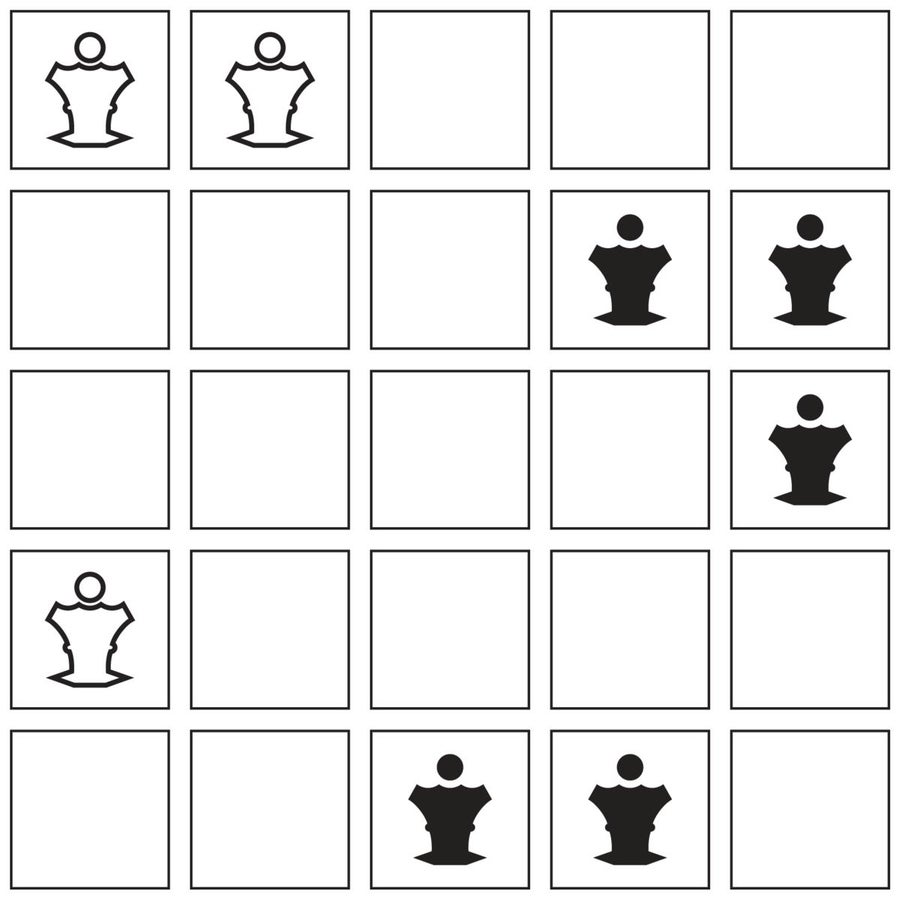
[答案:]