2015年10月,我在萬那杜維拉港一所法國高中培訓數學教師的時間即將結束。校長邀請我分享卡瓦酒,這是該國的一種傳統飲品。正如萬那杜的每位社會科學家所發現的那樣,分享卡瓦酒是學習的絕佳機會。這種飲料是用同名樹木的根製成的,可以使飲用者放鬆身心,暢所欲言。
第一次接觸卡瓦酒也是我接觸沙畫的開始。那天晚上,一位學員拿出一塊鋪滿細沙的大板子。在仔細地將表面弄平後,他畫了一個水平和垂直線的網格。然後,他開始在沙子上描繪溝壑,手指從不抬起。藝術家完成後,他用比斯拉馬語解釋說:“Hemia hem i wan fis i ronwe i stap unda ston from i kat wan sak,” 意思是“這是一條躲在石頭下以躲避鯊魚的魚。”
線條的流暢性,加上卡瓦酒的作用,使我陷入了驚奇的狀態。這項技術讓我想起了用一筆畫出複雜圖形的經典挑戰,筆不能抬起,也不能在同一條線上重複走兩次。它也使我想起了數學中的“尤拉圖”,它涉及一條遍歷每條邊恰好一次,並在同一點開始和結束的路徑。
支援科學新聞事業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和思想的有影響力的故事的未來。
當我思考這些想法時,一位實習生走近我,低語道:“老師,這幅畫中的數學在哪裡?” 儘管他不可能知道,但這句話將塑造我未來六年的生活,包括我關於沙畫的博士研究。一個問題尤其啟發了我:這些圖畫是如何創作出來的?

沙畫是用單指筆畫繪製的複雜圖形。 來源:阿爾班·達·席爾瓦
我的調查比我能想象的還要深入。透過觀察沙畫專家,瞭解他們的方法,收集圖畫和歷史,以及探索20世紀民族學家的工作,我開發了一個沙畫的數學模型。我的工作表明,這些藝術品可以被建模為演算法和代數性質運算的結果。事實上,數學語言被證明適合描述沙畫專家的工作。此外,沙畫可以幫助我們理解萬那杜社會與其環境之間維持的關係。
一種傳統藝術
萬那杜是一個群島國家,人口約31.5萬人,分佈在83個島嶼上。該國是世界上語言密度最高的國家,擁有138種本土語言。學校教授的兩種官方語言是法語和英語。比斯拉馬語,或比奇拉馬語,一種在萬那杜使用的英-美拉尼西亞混合語,是通用語言。
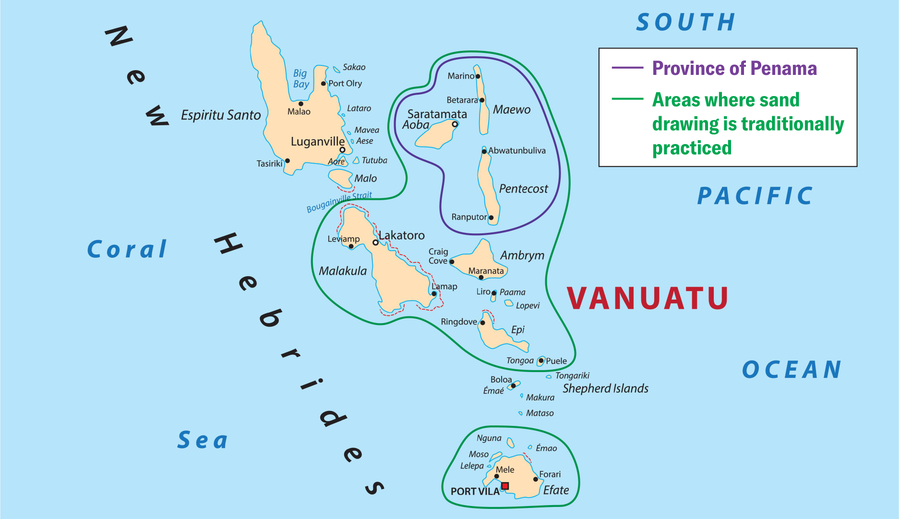
地圖顯示了萬那杜群島國家的一部分。民族數學家阿爾班·達·席爾瓦研究了該國佩納馬省的沙畫,特別是在馬埃沃島和彭特科斯特島上。來源:Rainer Lesniewski/Alamy Stock Vector (地圖); Amanda Montañez (綠色和紫色輪廓及圖例)
該國北部和南部的文化各不相同,即使在同一個島嶼內也是如此。例如,沙畫習俗僅在一些中部島嶼廣泛流傳。雖然這種傳統讓人想起印度泰米爾納德邦在泥土上所作的繪畫,但在許多方面它是獨一無二的。2008年,聯合國教科文組織將萬那杜的沙畫列為人類非物質文化遺產的一部分。
我的研究基於2018年在馬埃沃島和2019年在彭特科斯特島進行的兩次實地調查,特別關注彭特科斯特島北部拉加地區(發音為“拉-拉”)的人們所作的繪畫。這些島嶼與奧巴島一起構成了佩納馬省,並受共同傳統的約束,這極大地促進了我的研究。
“沙畫”,或比斯拉馬語中稱為sandroing,可能已有數千年的歷史。傳統上,它指的是一個人用手指在夯實的土地、沙灘或灰燼中繪製一條連續的閉合線。(這裡的“連續”和“閉合”與數學中的含義相同:沙畫類似於平面上的閉合連續曲線。)這條繪製的線受到線條或點的複合網格的約束。網格可以是矩形或圓形。
雖然很難知道有多少種設計在使用,但很明顯,隨著時間的推移,新的設計會出現,而另一些則會消失。一個非常接近智慧財產權的系統保護著這些圖畫,使得有時難以敏感地獲取這種傳統知識,並且具有挑戰性。
這些藝術品在其意義上是多維的。一些具有代表性的動物、昆蟲或植物圖畫與這些社會的信仰、宇宙起源、社會組織甚至傳統密切相關——這些傳統被統稱為卡斯托姆。這些圖畫也可以支援敘事;它們揭示了萬那杜中部社會的倫理或政治層面。在許多情況下,每種設計都有一個與這些不同方面相關的本土名稱。

一幅沙畫描繪了一條魚躲在石頭下以躲避捕食者。 來源:阿爾班·達·席爾瓦
今天,這些社會將這種習俗視為一種傳統的圖形藝術,有助於人們回憶起儀式、宗教和環境知識。此外,我在拉加地區遇到的一位酋長傑夫·託達利向我解釋說,藝術家是代言人:“在圖圖拉尼[白人外國人]到來之前,彭特科斯特北部的人們不知道如何說話。他們透過手指在地上描繪的圖畫來表達自己。不是人在說話,而是岩石、石頭、山丘和山谷的地面、風、雨、海水在說話。但現在情況顛倒了。是人在說話,而大地、風、雨和大海沉默了。現在[拉加地區的人們]有時會說,‘我們必須為土地說話,因為它不能再為自己說話了。’”
最後,這種短暫的藝術——每幅畫一旦完成就會被擦除——激發了講故事。從業者通常會將他們的圖畫與故事講述結合起來,而最有天賦的人能夠在繪畫的同時做到這一點。他們透過新增與他們的歷史相關的細節,包括熟悉的地方、人物、動物甚至蔬菜,來吸引觀眾的想象力,這並不罕見。
專家和規則
存在不同的專業知識和實踐水平。有些人根本不練習沙畫。另一些人則知道一些相當簡單的圖畫。“專家”——由他們社會的其他人指定——擁有令人印象深刻的曲目(根據一些人的說法,多達400幅圖畫)。雖然最早關於沙畫的民族誌提到這種藝術是男性專屬的,但今天情況並非如此。我遇到的一些女性擁有很高的專業水平。
從初學者到專家,每個人都遵循一套“規則”。由於這些社群具有口頭傳統,因此沒有書面記錄,但在我的實地調查期間,我列出了一份在大多數情況下都遵循的原則清單。所有圖畫都從一個網格開始,該網格提供支援並定義一組節點或交叉點和線條。
一個動畫展示了經典的龜形沙畫設計。 來源:阿爾班·達·席爾瓦
然後,規則指示允許的移動。更準確地說,藝術家必須 (1) 從一個節點移動到另一個節點,而不會穿過相同的路徑或在節點以外的地方切割網格,並且 (2) 必須在不抬起手指的情況下返回起點。
我在實地發現了一條額外的規則,事實證明這條規則對我的模型至關重要,如下所述。
瑪西亞·阿舍的直覺
我不是第一個認識到這些規則與數學概念相似的人。事實上,我的論文是美國數學家瑪西亞·阿舍在 20 世紀 80 年代進行的工作的延續,瑪西亞·阿舍是民族數學的先驅。她認為,在沙畫中,與數學家所稱的圖論,特別是與尤拉圖,存在明顯的聯絡。
為了理解阿舍的觀點有多麼革命性,請考慮在她和她的同代人工作之前,學者們普遍認為只有擁有文字的社會才能真正實踐數學。他們將對數學知識的調查限制在文字資料上,而忽略了在不使用書面語言的口頭傳統社會中看到的許多其他實踐。
但自從民族數學出現以來,一些學者已經開始推翻這些假設。這種轉變無疑始於 20 世紀 40 年代,當時數學家安德烈·韋伊在人類學家克勞德·列維-斯特勞斯的著作《親屬關係的基本結構》中一篇現在著名的附錄中證明,澳大利亞 Yolngu 人的親屬關係規則遵循所謂的非平凡群定律。從那時起,研究人員在許多其他地方發現了數學原理,包括馬達加斯加的播種遊戲和占卜、巴布亞紐幾內亞特羅布裡恩群島的線繩遊戲、安第斯山脈的紡織品和留尼汪島的裝飾性窗簾。
阿舍關於沙畫的工作借鑑了一位年輕的民族誌學家伯納德·迪肯的工作,他在 1926 年和 1927 年從萬那杜的馬萊庫拉島和安布里姆島收集並轉錄了 100 多幅沙畫。阿舍研究了這些圖形,並意識到這些影像可以用數學來描述。
每幅沙畫都可以被認為是一個“圖”,因為它包含頂點或點,由邊或線連線。(圖中“圖”的定義在數學中是特殊的。在圖論中,圖是由頂點和邊組成的簡單圖形,用於繪製網路中許多節點的連線——例如,道路連線的城市、網際網路連線的計算機,甚至社交關係連線的人。)
阿舍觀察到,在沙畫中,沙子上描繪的線條可以比作一個圖,其頂點包括圖案中建立的所有交叉點。邊是這些頂點之間的所有弧。這些圖也是尤拉圖,這意味著沙畫藝術家必須只訪問每條邊一次,並且必須返回起點。阿舍還記錄了每個頂點的邊數,數學家稱之為頂點的“度”。這很重要,因為根據數學家卡爾·希爾霍爾澤建立的尤拉定理,一個連通圖是尤拉圖,當且僅當每個頂點都具有偶數度。
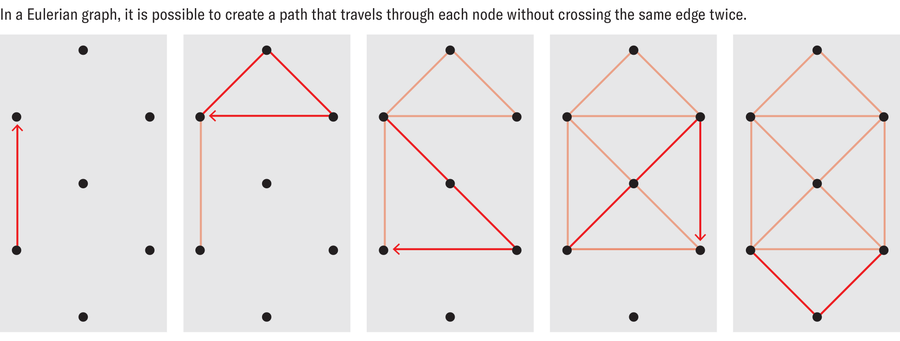
來源:阿爾班·達·席爾瓦/Pour la Science,由阿曼達·蒙塔涅斯重新設計
阿舍從未有機會去萬那杜親眼看看設計師的工作,這無疑限制了她的研究。因此,我自己的研究可以更進一步。阿舍的一個特殊觀察結果推動了我對這些影像是如何建立的研究。透過檢查迪肯的圖畫,她觀察到其中一些圖可以分解為三到四個子步驟,當這些子步驟連線在一起時,就形成了最終的圖畫。換句話說,每個步驟都產生一個返回起點的子圖。當這些子圖疊加在一起時,最終的圖畫就顯現出來了。我將這種識別子圖的過程稱為“分解”。
這些子圖為我的工作提出了幾個問題:每幅圖是否都可能進行這種型別的分解?這些層是如何組合在一起的,順序重要嗎?最重要的是,這些層對沙畫藝術家代表什麼?
為了進行調查,我首先試圖改進阿舍提出的圖模型,然後確定計算機是否可以生成沙畫的自動分解。阿舍曾提出用一組受變換(例如旋轉、平移、對稱和反演)影響的模式來建模沙畫。但是在聽取沙畫創作者的意見時,我意識到變換在其設計執行中並沒有發揮根本性的作用。事實上,無論圖案在網格上的方向如何,他們都使用相同的術語來表示圖案。因此,我需要另一種方法來描述這些沙畫藝術家的做法。
藝術家本人幫助了我完成這項工作。圖對於建模物件(頂點)之間的一組關係(邊)非常有用。但在她的工作中,阿舍沒有考慮這些關係的性質。透過強調網格的節點、圖的頂點和邊緣處的曲線,她忽略了藝術家將如何從一個峰值移動到另一個峰值。在詢問專家時,我觀察到,對於他們來說,運動的方向與節點一樣重要:設計師的手指從一個節點移動到另一個節點,從初始方向移動到最終方向,因此節點在被穿過時,根據兩條可能的對角線中的一條或另一條,發揮著不同的作用。
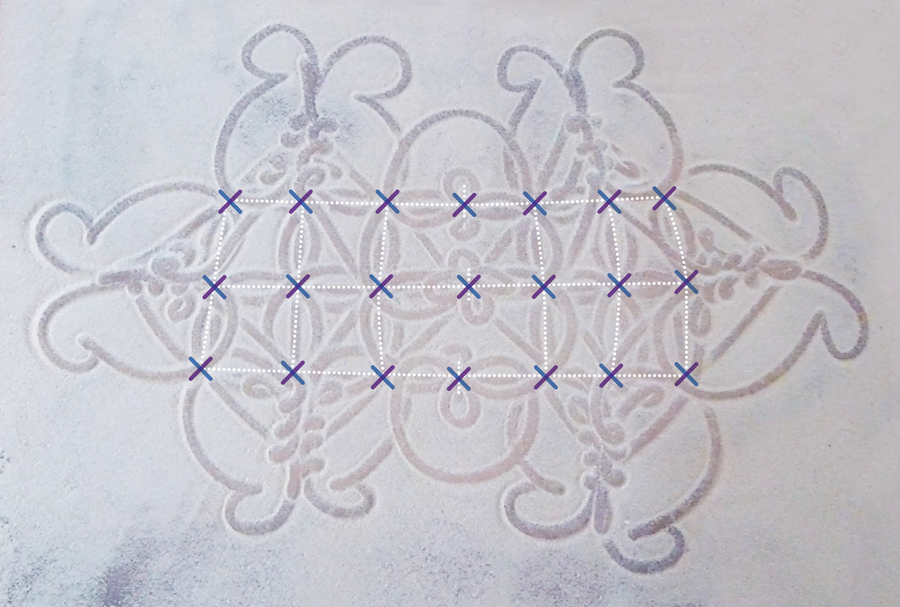
在這幅沙畫中的每個節點或交叉點,手指都採用兩條對角線路徑之一(紫色和藍色)。 來源:阿爾班·達·席爾瓦/Pour la Science,由阿曼達·蒙塔涅斯重新設計
因此,為了用圖來建模沙畫設計,可以建立一個圖,其中網格的每個節點都被視為兩個頂點,而不是一個頂點,每個頂點都被分配給一條對角線。因此,我們獲得了一個新的圖——命名為 Gmod ——其頂點不是阿舍提出的網格的節點 S ,而是成對的 ( S , d )。
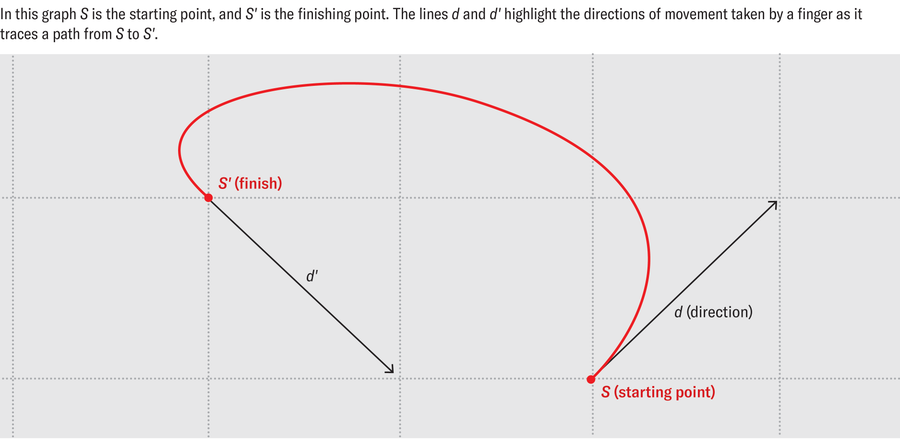
來源:阿爾班·達·席爾瓦,由阿曼達·蒙塔涅斯重新設計
在這個圖中, d 是所採取的方向,並且從 S 沿方向 d 出發並在方向 d’ 到達 S’ 的每個繪畫動作都對應於頂點 ( S , d ) 和 ( S’ , d’ ) 之間的邊。而這個結果 Gmod 圖仍然是尤拉圖!
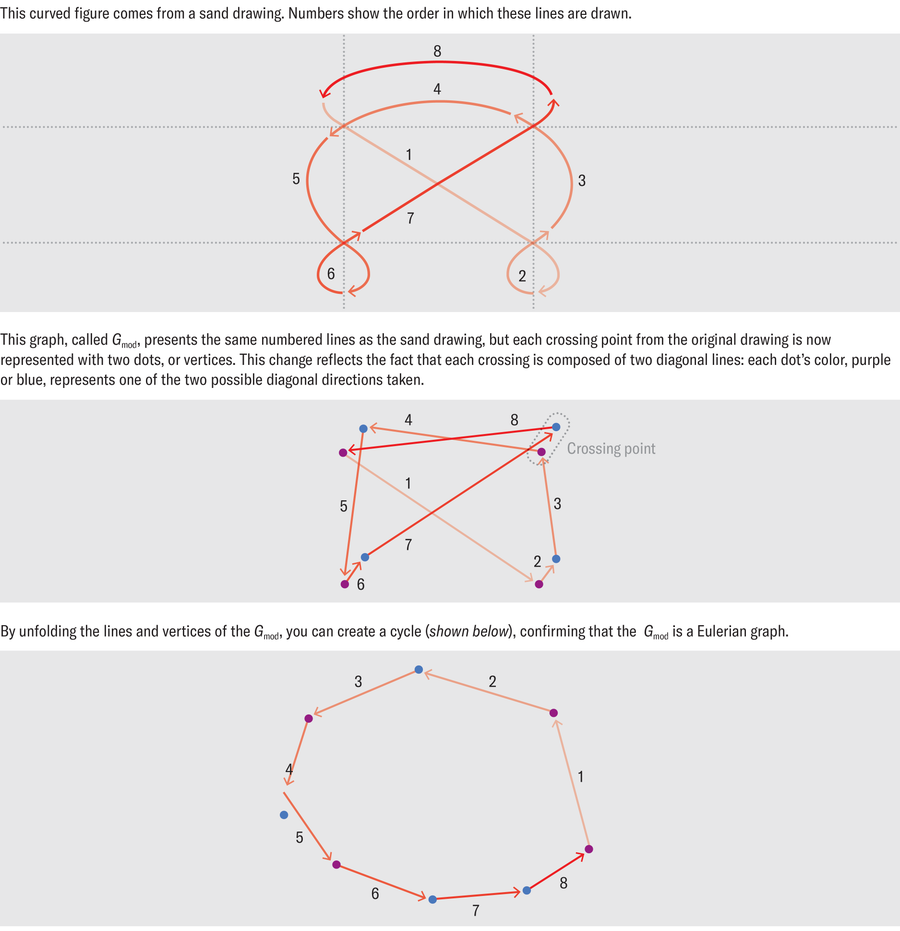
來源:阿爾班·達·席爾瓦,由阿曼達·蒙塔涅斯重新設計
在圖畫中發現的定理
1912 年,數學家奧斯瓦爾德·維布倫在後來被稱為維布倫定理的定理中確定了尤拉圖的另一個特徵:一個圖是尤拉圖,當且僅當它可以分解為不相交的環的並集。在圖論中,“環”一詞指的是一系列不同的連續邊,其起點和終點頂點相同。
事實證明,Gmod 圖的環對應於沙畫的環,因此沙畫可以分解為環的不相交併集。
這種方法是否使我們遠離了沙畫師?我認為不會。相反,環可以為更好地理解他們的方法提供關鍵。在我收集的 60 幅左右的圖畫中,我注意到藝術家有時會在完成一個環時暫停繪畫。此外,當沙畫師被迫尋找另一條路徑(比斯拉馬語中的 rod )時,他們傾向於重新排列他們在繪畫中使用的典型環順序,或者嘗試找到另一種分解為環的方式。
最後,一些環有本土名稱,這表明它們對於藝術家來說就像積木一樣。事實上,這種對圖環的關注似乎也呼應了伴隨圖畫的故事,這些故事在萬那杜社會理解世界的方式中發揮著根本性的作用。在我的研究中,我還提出,一些環分解可能與這些社會構想他們與非人類關係的方式有關。
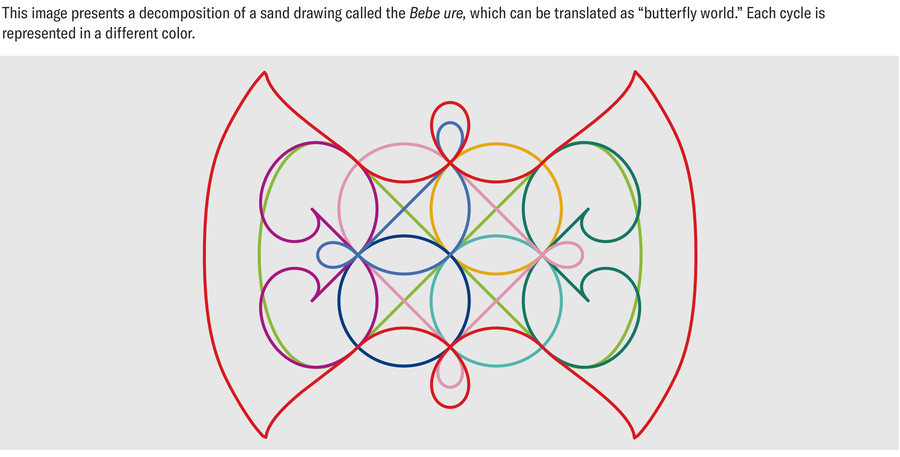
來源:阿爾班·達·席爾瓦
這些結果引發了關於數學的普遍性以及數學在其他文化中採取的形式的問題。它們也為數學教學開闢了前景。自 2010 年以來,獲取沙畫等傳統知識一直是萬那杜學校的目標之一,並且是更大的教育去殖民化運動的一部分,就像夏威夷和法國領地新喀里多尼亞的努力一樣。然而,在當前的學校課程中,沙畫與數學之間沒有建立聯絡。為此,萬那杜人皮埃爾·梅桑,新喀里多尼亞大學教育學博士生,正在研究沙畫的實踐是否可以支援數學教學。我們可以期待他在未來幾年從這項調查中學習到的東西。
本文最初發表於 Pour la Science,並經許可轉載。
