數字有很多不同的型別,您可能還記得在學校學到的一些:自然數、有理數、無理數、虛數、可計算數和不可計算數。然而,今天,我們將要談論一些令人愉快的事情,即“快樂數”。是的,它們確實出現在數學中,而且這真的是它們的專業名稱。
快樂數沒有任何實際應用,但它們確實具有驚人的特性,這就是它們在業餘數學家中如此受歡迎的原因。例如,所有自然數都可以分為“快樂”數或“悲傷”數。“快樂”的概括導致了“自戀數”,它們非常專注於自身。
快樂數的概念最初是誰提出的尚不清楚。 它們在 20 世紀 60 年代由英國數學家雷金納德·艾倫比普及開來:取任意自然數,例如 13,將其數字平方(12 = 1;32 = 9)並將它們相加(1 + 9 = 10)。然後對結果數字重複此快樂計算(12 + 02 = 1)。如果第二次運算的總和為 1,則您已達到“不動點”。也就是說,每次進一步執行相同的過程都將始終產生結果 1。透過重複快樂計算最終產生 1 的數字稱為快樂數。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
因此,人們不得不稱所有其他數字為悲傷數。令人興奮的是,當您應用快樂計算時,悲傷數也遵循固定的模式。例如,讓我們從 4 開始:42 = 16,16 將產生 37(12 = 1 和 62 = 36 的和)。如果我們保持這種模式,我們將得到 16 → 58 → 89 → 145 → 42 → 20 → 4。因為我們從 4 開始快樂計算,所以數字序列重新開始。因此,如果一個數字的重複快樂計算產生值 4、16、37、58、89、145、42 或 20,則該數字註定是悲傷的。艾倫比立即想知道自然數是否都可以分為快樂數(最終結果為 1)或悲傷數(以 4 開頭的迴圈的一部分)——或者快樂計算是否還有其他終點。
有一種快速的方法可以找出答案。為此,您首先需要檢查一個數字的平方數字之和可以變得有多大。假設您有一個一位數,例如 9。它的平方 81 大於它本身。對於兩位數(例如 99)也是如此:92 + 92 = 162。但是,對於三位數或更多位數的數字,情況並非如此。即使對於 999,其數字平方之和也小於數字本身,即 243。這意味著如果您對一個三位數重複執行快樂計算,您將只會得到三位數值。另一方面,如果您從四位數開始,則第一步的快樂計算將導致三位數結果。
悲傷數演算法
要證明每個自然數要麼是快樂數,要麼是悲傷數,您必須遍歷所有三位數。這項任務很繁瑣,但並不特別複雜。例如,您可以建立一個簡短的演算法來輔助以下步驟的過程
1. 為 i、j 和 k 選擇一個從 0 到 9 的值。
2. 計算 z = i2 + j2 + k2。
3. 如果 z = 1,則三位數 ijk 是快樂數。
4. 如果 z = 4、16、37、58、89、145、42 或 20,則 ijk 是悲傷數。
5. 如果兩種情況都不是真的,則使用“向下取整函式”Floor(x) 設定 i、j 和 k 的新值,該函式將每個十進位制數分配給其向下取整的整數值 (Floor(1.6) = 1):i = Floor(z⁄100),j = Floor(a – 100 x i⁄10),k = a – i x 100 – j x 10。使用 i、j 和 k 的這些新值,從步驟 2 繼續該演算法。
對 i、j 和 k 的所有一位數值重複此演算法,結果將始終是快樂數或悲傷數。換句話說,所有三位數要麼是快樂數,要麼是悲傷數——所有四位數也是如此,因為它們的平方數字之和(快樂計算的第一步)將產生一個三位數。
這個論點可以一直延續到更大的自然數。結果是,每個自然數要麼是快樂數,要麼是悲傷數。當重複使用快樂計算時,沒有哪個值可以逃脫這些命運。
但專家們對這個結果並不滿意。例如,數學家們還想知道,快樂數的百分比是多少?它們是否畫素數一樣隨著大小的增加而變得稀有,或者它們是否總是以大致相同的頻率出現?
首先,快樂數有無限個。畢竟,10 的每個冪,10x, 都必然對應一個快樂數。
但是它們的密度 ρ 呢,即快樂數與所有自然數的比率?在前 10 個自然數中,有三個快樂數(ρ = 0.3)。在前 100 箇中,有 20 個(ρ = 0.2)。在前 1,000 個自然數中,有 143 個快樂數(ρ = 0.143)。甚至在線上整數序列百科全書 (OEIS) 中 也有一個條目專門處理快樂數在 0 到 10n 區間內的頻率。因此,如果您計算不同 n 次冪的密度,您將得到以下圖片
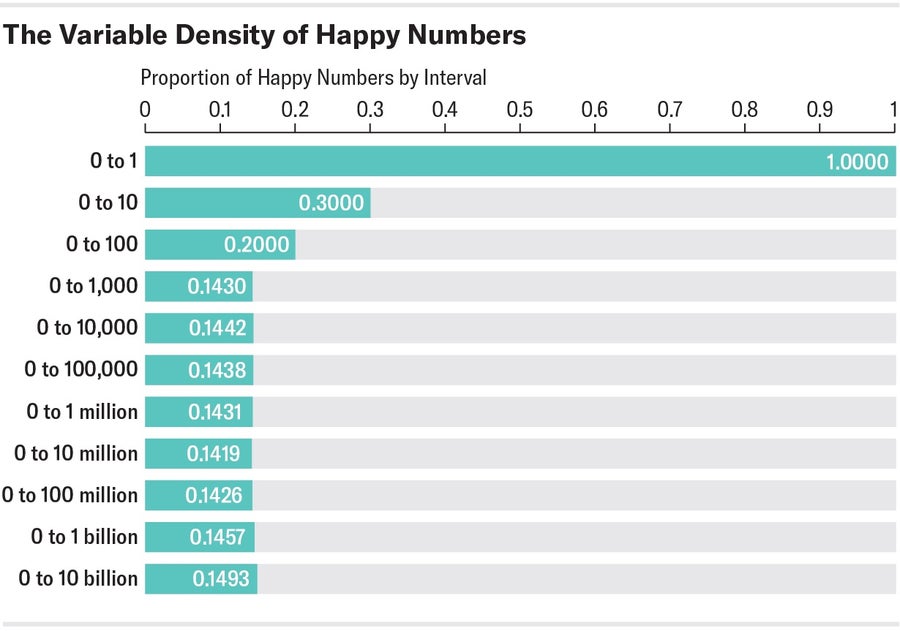
快樂數與給定區間內所有其他數字的比率稱為快樂數的密度。 來源: Spektrum der Wissenschaft,由 Amanda Montañez 設計
現在人們可能會假設密度大約等於 14%。 但正如數學家賈斯汀·吉爾默在 2011 年的一篇預印本論文中證明的那樣(該論文隨後於 2013 年發表),快樂數沒有明確定義的密度。他證明,它們的密度取決於所考慮的區間,並且不會收斂到固定極限。 儘管這個結果讓很多人感到驚訝,但快樂數遠非唯一沒有固定、明確密度的數字。
例如,在所有以 1 開頭的數字集合中也發現了這種行為。在前九個數字(1、2、3、4、5、6、7、8、9)中,只有一個以 1 開頭(數字 1),這對應於 1⁄9 的密度。在前 19 個數字(1、2、...、10、11、12、...、19)中,有 11 個以 1 開頭,密度為 11⁄19。在前 99 個數字中,仍然有 11 個以 1 開頭,因此在此數字區間內的密度為 11⁄99 = 1⁄9 。在前 199 個數字中,有 110 個以 1 開頭,因此密度為 110⁄199,依此類推。
密度在較高值和較低值之間波動,具體取決於您選擇的區間。在這種情況下,無法給出整個自然數範圍內密度的極限。快樂數也是如此。根據區間,它們的密度在低於 12% 到高於 18% 之間變化。
計算連續快樂數
數學家們關注的另一個問題是:可以有多少個連續的快樂數?前兩個是 31 和 32。要找到前三個連續的快樂數,您必須檢視四位數的值:1,880、1,881、1,882。
在 2006 年的一篇預印本論文中,數學家郝潘證明 存在任意數量的連續快樂數。(該論文隨後於 2008 年發表。)關鍵是您可能必須搜尋很長時間。在 7,839 可以找到一個包含四個連續數字的序列,在 44,488 可以找到一個包含五個數字的序列,在 7,899,999,999,999,959,999,999,996 可以找到一個包含六個數字的序列。
另一個謎題是考慮將快樂數變為 1 需要多少次快樂計算。 這個量可以用來定義一個數的整體快樂程度。迭代次數越少,數字越快樂。因此 1、10、100 等非常快樂,而 13 則略遜一籌。
哪個數是最不快樂但不是悲傷的數?在兩位數中,它是 7。從 7 到 1 需要五次迭代。接下來是 356,您需要六次快樂計算才能得到它。
在那之後,事情變得瘋狂起來。如果您想要一個更不快樂的數字,您最終會得到一個 977 位數的值:378899999...999。迭代九次的快樂數有 10977 位數——而且從外觀上看,迭代次數沒有限制。可以為任意數字 n 找到一個快樂數,它僅在重複 n 次快樂計算後才產生 1。因此,不快樂的程度沒有限制。
當人們概括快樂數的概念時,事情變得非常令人興奮。除了對數字平方求和之外,您還可以加上三次方。在這種情況下,自然數不再分為兩個陣營,而是分為九個陣營。迭代要麼在 1 處結束(“快樂立方體”),要麼在其他四個不動點之一處結束(153、370、371、407),要麼在四個迴圈之一中結束:55 → 250 → 133 → 55;160 → 217 → 352 → 160;136 → 244 → 136;或 919 → 1,459 → 919。
迴歸自身的數字
這種概括引出了數論中的另一個概念。當一個數字由 n 位數字組成時,您可以計算其數字的 n 次冪之和。例如,對於 243,結果是:23 + 43 + 33 = 8 + 64 + 27 = 99。對於某些數字,此計算的結果會使其自身迴歸。例如 153,因為 13 + 53 + 33 = 153。這樣的數字稱為自戀數。
所有個位數都是自戀數。事實上,自戀數總共只有 89 個:0、1、2、3、4、5、6、7、8、9、153、370、371、407、1,634、8,208、9,474、54,748、92,727、93,084、548,834,...,最大的是 115,132,219,018,763,992,565,095,597,973,971,522,401。
可以證明,透過估算,沒有比這更大的自戀數。假設一個數字有 n 位數字。如果所有數字的值都為 9,則數字的 n 次冪之和的最大大小為:n x 9n。但是,當 n 超過一定大小時,此結果始終小於由 n 位數字組成的最小數字 (10n–1)。因此,這樣的數字不可能成為自戀數。
過渡發生在 60 位數時:雖然 60 x 960= 1.08 x 1059 並且因此大於 1059,但 61 x 961= 0.99 x 1060 並且小於 1060。對於所有 n > 60 都是如此。因此,不可能存在由超過 60 位數字組成的自戀數。透過遍歷從 0 到 60 位數字的所有數字,可以測試它們的自戀性。事實證明,只有 89 個。
由於自戀數的數量有限,因此與快樂數相比,它們持有的未解決問題要少得多。但是這兩個類別都非常適合有趣的消遣。
本文最初發表於 Spektrum der Wissenschaft 並經許可轉載。
