當我們的孩子還小時,我們花了很多時間一起在廚房裡。我們利用這些機會偷偷地教他們關於科學的知識:熱和溫度、流體流動、密度、粘度、物理變化、化學反應、酸和鹼。我們告訴他們這些性質如何結合起來神奇地使蛋糕透過二氧化碳膨脹;我們告訴他們關於酵母和其他有趣的微生物。
我們也談論數學:重量和測量、面積和體積。披薩是介紹分數的絕佳方式。我們喜歡一起烤餅乾,並使用了許多不同的餅乾切刀。我們的兒子喜歡恐龍,所以我們有恐龍餅乾切刀,還有花、心、星星和動物。當我們使用餅乾切刀時,出現了一個有趣的難題:它們在我們切出的每個形狀之間留下了空隙。為了用完所有的麵糰,必須重新擀麵。但之後麵糰會變暖,必須冷藏後才能再次切割。這很耗時。
一定有更有效率的方法來分割麵糰。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
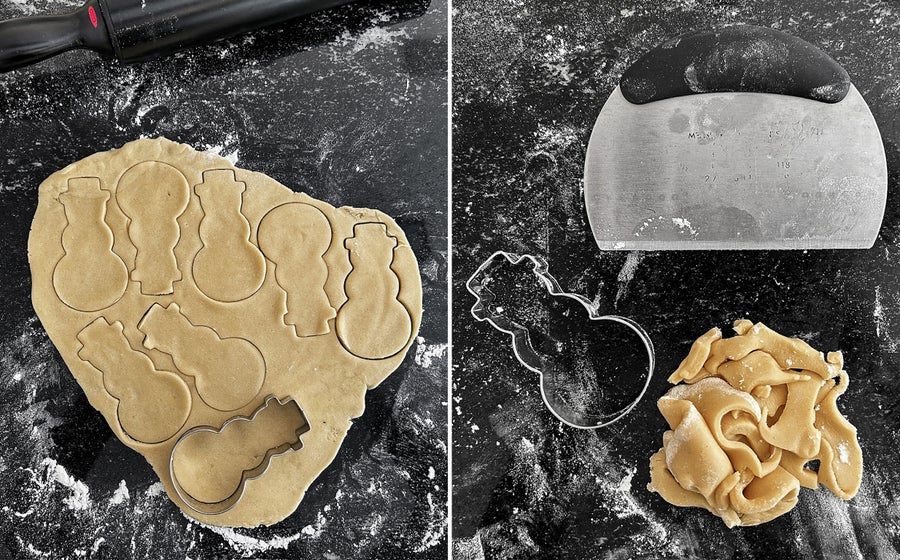
使用更傳統的餅乾切刀製作餅乾通常會留下很多剩餘麵糰。
梅加·薩蒂亞納拉亞納
作為一名數學家,我聽說過平鋪和鑲嵌,它們指的是使用一個或多個幾何形狀覆蓋表面,沒有重疊和空隙。這就是餅乾切刀問題的答案!
所以我尋找鑲嵌餅乾切刀,但只找到了正方形和六邊形。它們有效,但就形狀而言,並不是特別有趣。然後,大約 15 年前,第一批 3D 印表機問世了。有可能製作定製餅乾切刀,然後就變成了選擇形狀的問題。許多圖形可以用來鑲嵌,例如正三角形或不規則三角形、矩形或一些不規則五邊形。一些不規則五邊形是由已故的業餘數學家馬喬裡·賴斯發現的,可以在Mathemalchemy中看到,這是一個藝術和數學展覽,合作者包括杜克大學數學家英格麗·多貝西和紡織藝術家多米尼克·埃爾曼。該展覽還展示了一個使用 π 符號的鑲嵌餅乾切刀,由多貝西進行了適當的調整。
還有其他例子;伊斯蘭藝術包括使用五邊形對稱的美麗而富有創意的設計。
如果我們連線兩個或多個圖形,那麼會有更多選擇。例如,八邊形和正方形,或五邊形和菱形,或 M.C. 埃舍爾的所有驚人作品。但並非所有都適合製作餅乾;我們製作了一個埃舍爾蜥蜴形狀的餅乾切刀,但當我們將圖形分開時,腿斷了。
所有這些鑲嵌都是週期性的,這意味著它們具有重複的圖案。在 20 世紀 70 年代,羅傑·彭羅斯發現了兩種稱為風箏和飛鏢的圖形,如果遵守一些區域性規則(指定飛鏢的哪些邊可以相互接觸),它們只能非週期性地平鋪平面(意味著所有可能的配置都是非週期性的)。但如果不遵守規則,那麼它們就會週期性地平鋪。這非常適合餅乾切刀,因為生麵糰是週期性平鋪的,然後餅乾可以週期性或非週期性地放置。有關彭羅斯平鋪的更多資訊,請參見影片頻道Veritasium和一個名為“彭羅斯型伊斯蘭交錯圖案”的網頁。

鑲嵌餅乾切刀,例如這種風箏和飛鏢形狀的切刀,可以建立漂亮的圖案,並且比其他形狀使用更多的麵糰。
梅加·薩蒂亞納拉亞納
幾年前,在我的朋友們的幫助下,我使用 3D 列印機制作了一個風箏和飛鏢形狀的餅乾切刀,它們以週期性方式平鋪在一起。烘烤後,這些塊可以週期性或非週期性地放置。這效果非常好。
然後,“帽子”出現了。
大約 50 年來,數學家們一直在思考是否可能存在一個可以非週期性地平鋪平面的單一圖形。在 2023 年,大衛·史密斯、克雷格·卡普蘭、柴姆·古德曼-施特勞斯和塞繆爾·邁爾斯設法找到了難以捉摸的非週期性單片平鋪,他們稱之為“帽子”或“愛因斯坦”。
我的第一個衝動是製作一個帽子形狀的餅乾切刀。事實證明,在沒有空隙或重疊的情況下放置這些塊非常困難。但是,發現帽子的人實際上也意識到它可以轉化為無限數量的非週期性單片平鋪,正如克雷格·卡普蘭報道的那樣。其中三個單片平鋪可以週期性和非週期性地平鋪,它們非常適合作為餅乾切刀。
史密斯和他的團隊稱之為“Tile (0,1)”的人字形很容易製作,易於在麵糰上使用,並且烘烤好的餅乾很容易以美麗的圖案放置,尤其是在用不同顏色裝飾時。另一個完美的候選者是作者稱之為“Tile (1,1)”的圖形。當與映象結合時,該圖形週期性地平鋪,但如果不允許映象,則僅非週期性地平鋪。因此,完美的餅乾切刀有兩個這樣的圖形,一個正常,一個反射。
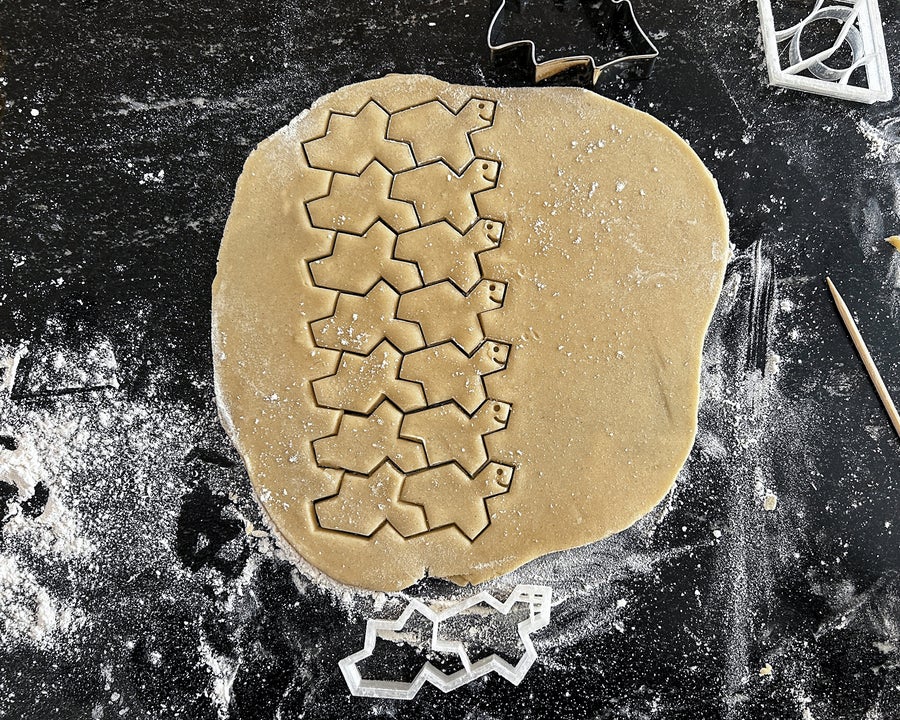
基於大衛·史密斯發現的帽子的餅乾切刀可以製作鑲嵌圖案,從而最大限度地減少麵糰浪費。
梅加·薩蒂亞納拉亞納
史密斯和合作者還發明瞭一類彎曲的非週期性單片平鋪,他們稱之為“幽靈”,它也可以變成餅乾切刀,最近發現的軟細胞也可以。在每種情況下,如果您小心,您可以切割您的餅乾麵糰,最大限度地減少重新擀麵和浪費。
當您在節日期間烹飪和烘烤時,如果您能找到一個鑲嵌餅乾切刀,並且如果您讓您的孩子參與進來,您可以利用您本會花費在重新擀麵團上的時間來告訴他們關於科學和數學的知識。在我們的例子中,我們的孩子已經長大,但我的鑲嵌餅乾切刀系列和我都很高興在我們的孫子孫女到來時分享數學和科學的奇蹟。
這是一篇觀點和分析文章,作者或作者表達的觀點不一定代表《大眾科學》的觀點。
