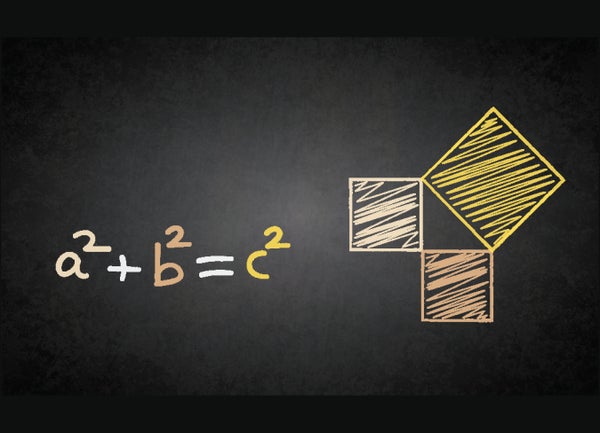兩名高中生以一種 20 世紀早期數學家認為不可能的方式證明了勾股定理:使用三角學。
Calcea Johnson 和 Ne’Kiya Jackson 都在新奧爾良的聖瑪麗學院就讀,她們上個月在美國數學學會的一次會議上宣佈了她們的成就。“老實說,這是一種無與倫比的感覺,因為沒有什麼能與之相比,能夠做一些……人們認為年輕人做不到的事情,”約翰遜告訴 WWL-TV,新奧爾良 CBS 分支機構。
如果得到驗證,約翰遜和傑克遜的證明將與數學家和教育家伊萊沙·盧米斯相矛盾,後者在他的 1927 年著作勾股定理中指出,勾股定理的任何三角證明都不可能是正確的。 她們的工作與多年來新增到數學檔案中的其他一些三角證明相呼應。 每一種方法都避開了“迴圈邏輯”,從而證明了這個關鍵定理。 那麼,勾股定理的三角證明究竟是什麼?為什麼盧米斯如此排斥這個想法?
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
勾股定理提供了一個方程,透過將其他兩條邊的平方相加來計算直角三角形的較長邊。 它通常表示為 a2 + b2 = c2。 在這個方程中,a、b 和 c 代表直角三角形三條邊的長度,直角三角形是指兩條邊之間有一個 90 度角的三角形。 量 c 是最長邊的長度,稱為斜邊。 雖然該定理以古希臘哲學家畢達哥拉斯的名字命名,但一些歷史學家認為早在大約 1000 年前巴比倫就已知道該定理。
德克薩斯農工大學-商業分校的榮譽數學教授斯圖爾特·安德森說,該定理“將代數和幾何聯絡起來”。 “語句 a2 + b2 = c2,這是一個代數語句。 但它所來自的圖形是一個幾何圖形。”
與此同時,三角學側重於取決於角度的函式。 這些函式,如正弦和餘弦,是使用直角三角形定義的。 想象一個直角三角形,其中一條邊平放在桌子上,另一條邊從它與第一條邊成直角相交的地方垂直向上。 斜邊將在這兩條邊之間呈對角線延伸。
現在測量斜邊和桌子之間的角度。 數學家將這個角的正弦定義為垂直邊的高度除以斜邊的長度。 這個角的餘弦是水平邊的長度除以斜邊。 因此,勾股定理等價於方程 sin2 x + cos2 x = 1。 “許多基本的三角‘恆等式’只不過是勾股定理,”安德森解釋說,他指的是描述不同三角函式之間關係的方程。
盧米斯認為,如果您在勾股定理的證明中使用了這些函式,那麼您就從一開始就假設了該定理——這是一個迴圈論證,因此是一個不可饒恕的數學錯誤。
但事實並非總是如此。 在他們在美國數學學會會議上的演講中,傑克遜和約翰遜表示,一種稱為正弦定理的三角恆等式不依賴於勾股定理,他們可以用它來證明該定理。
安德森希望傑克遜和約翰遜的證明能夠提高學生對數學的興趣。 “這讓我想,如果我還在教課就好了,這樣我就可以談論這件事了,”他說。
過去出現的其他勾股定理的三角證明包括數學家亞歷山大·博戈莫爾尼的網站上描述的一些證明。 其中一個證明是由當時的物理學家和本寧頓學院的數學家傑森·津巴撰寫的,並於 2009 年發表在Forum Geometricorum上。 該證明使用了一個三角恆等式,該恆等式允許您計算角 x – y 的餘弦和正弦,而無需使用勾股定理——如果您知道 x 和 y 本身的餘弦和正弦。
2009 年 10 月 26 日,博戈莫爾尼將津巴的證明新增到他的網站,並寫道“伊萊沙·盧米斯、我自己以及毫無疑問的許多其他人曾經並且仍然相信,勾股定理的三角證明是不可能的……我很高興承認自己錯了。” 隨著時間的推移,博戈莫爾尼在他的網站上添加了更多的三角證明:其中一個證明可以用短短四行字寫完。
這個傳奇故事表明,即使是最簡單的數學也可能讓我們感到驚訝。 安德森說:“我認為,數學家們已經學會了不要大膽聲稱某事是不可能的,因為多年來我們已經為此尷尬了太多次。”
美國數學學會已鼓勵新奧爾良的學生提交他們的證明以在同行評審的科學期刊上發表。