夏威夷大學的地球物理學家巴里·利納特提供了以下解釋。
我們首先確定地球的質量。艾薩克·牛頓的萬有引力定律告訴我們,兩個物體之間的引力與它們質量的乘積成正比,與它們質心之間距離的平方成反比。為了獲得合理的近似值,我們假設它們的地理中心就是它們的質心。
因為我們知道地球的半徑,我們可以使用萬有引力定律來計算地球的質量,以地球表面物體上的引力(其重量)為單位,並使用地球半徑作為距離。我們還需要萬有引力定律中的比例常數G。這個值是由亨利·卡文迪許在18世紀透過實驗確定的,即兩個各重一公斤且相隔一米的物體之間極小的力,為 6.67 x 10-11 牛頓。卡文迪許透過精確測量金屬球體之間的水平力,在一個有時被稱為“稱量地球”的實驗中確定了這個常數。
支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。

知道地球的質量和半徑以及地球與太陽的距離,我們可以再次利用萬有引力定律計算太陽的質量(右圖)。地球和太陽之間的引力是G乘以太陽的質量乘以地球的質量,再除以地球和太陽之間距離的平方。這種引力必須等於使地球保持在其(幾乎圓形)繞太陽軌道上所需的向心力。向心力是地球的質量乘以其速度的平方再除以其與太陽的距離。透過天文方法確定到太陽的距離,我們可以計算出地球繞太陽的速度,從而計算出太陽的質量。
一旦我們有了太陽的質量,我們就可以類似地確定任何行星的質量,方法是透過天文方法確定行星的軌道半徑和週期,計算所需的向心力,並將該力等同於使用太陽質量的萬有引力定律預測的力。
加利福尼亞州克萊蒙特市哈維·穆德學院的物理學家格雷戈裡·A·萊曾加提供了更多細節。
行星的重量(或質量)由其對其他物體的引力效應決定。牛頓萬有引力定律指出,宇宙中的每一塊物質都以引力吸引其他每一塊物質,該引力與其質量成正比。對於我們在日常生活中遇到的物體大小,這種力非常小,以至於我們沒有注意到它。然而,對於行星或恆星大小的物體,它非常重要。
為了利用引力來找到行星的質量,我們必須以某種方式測量其對另一個物體的“拉力”強度。如果所討論的行星有衛星(天然衛星),那麼大自然已經為我們完成了這項工作。透過觀察衛星繞其主行星執行所需的時間,我們可以利用牛頓方程推斷出行星的質量必須是多少。
|
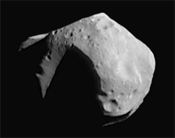
圖片來源:NEAR
小行星瑪蒂爾德的質量是透過測量 NEAR 航天器飛越過程中引力擾動來計算的。 |
對於沒有可觀測天然衛星的行星,我們必須更加聰明。雖然水星和金星(例如)沒有衛星,但它們確實相互施加微小的拉力,也對太陽系的其他行星施加微小的拉力。因此,行星遵循的路徑與沒有這種擾動效應時略有不同。儘管數學計算更加困難,不確定性也更大,但天文學家可以利用這些微小的偏差來確定沒有衛星的行星有多大質量。
最後,對於那些質量非常小以至於無法測量地擾亂其他行星軌道的物體(例如小行星)呢?在最近幾年之前,此類物體的質量只是估計值,基於明顯的直徑以及對這些物體可能礦物組成的假設。
然而,現在,幾顆小行星已經被(或即將被)航天器訪問。就像天然衛星一樣,飛越小行星的航天器的路徑會因小行星質量控制的量而彎曲。這種“彎曲”是透過地球上的仔細跟蹤和多普勒無線電測量來測量的。最近,NEAR 航天器飛越了小行星瑪蒂爾德,首次確定了它的實際質量。事實證明,它的結構比預期的要輕得多,也更“泡沫狀”,這一事實正在挑戰行星科學家們做出解釋。
最初發佈於 1998 年 3 月 16 日。