本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
數學可以幫助我們繪製真實物體。自然模式的規律性可以引導藝術家在藝術作品中使用數學概念。許多植物的葉子非常有趣和美麗,並且在它們的結構中可以找到一些數學模式。例如,螺旋蘆薈是一種來自賴索托的植物。螺旋蘆薈的葉子形成非常美麗的螺旋形。
有多種方法可以使用數學概念生成葉子形狀。一個著名的例子是巴恩斯利蕨。英國數學家邁克爾·巴恩斯利(Michael Barnsley,生於1946年)在他的著作《分形無處不在》中描述了這個美麗的分形。他的分形類似於蕨類植物的葉子。他使用迭代函式系統方法建立了這個分形。
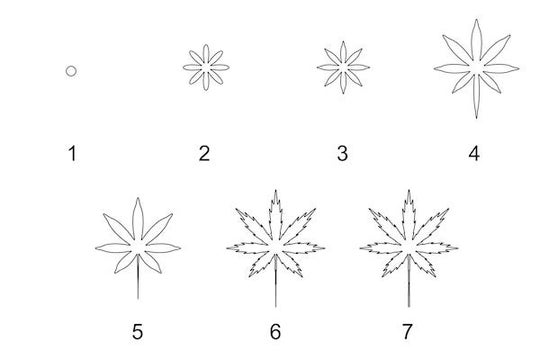
用數學公式繪製日本楓葉。致謝:Hamid Naderi Yeganeh
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
您可能會認為下面影像中的葉子是手工繪製的。但它們實際上是計算機生成的數學圖形。這些形狀是使用三角函式正弦和餘弦生成的。在這裡,我想談談我用來建立這些圖形的方法。
當我想繪製真實物體時,我會嘗試找到一個可以生成該圖形的數學公式。我使用逐步過程來找到這樣的公式。在該過程的每個步驟中,我嘗試透過向公式新增數學表示式來增加圖形與真實物體的相似性。通常,我會搜尋由正弦和餘弦函式生成的表示式。這兩個數學函式的屬性(特別是週期性、有界性和平滑性)使它們在該過程中非常有用。實際上,我需要在每個步驟中解決找到合適的數學表示式的問題。因此,某些步驟可能非常困難甚至不可能。例如,在上面的影像中,您可以看到生成類似於日本楓樹葉子的數學曲線的過程。該圖顯示了該過程如何將一個圓轉換為圖形。
這些影像顯示了使用上述方法建立的三個數學曲線。它們由引數方程描述
楓葉

楓葉。致謝:Hamid Naderi Yeganeh
日本楓葉
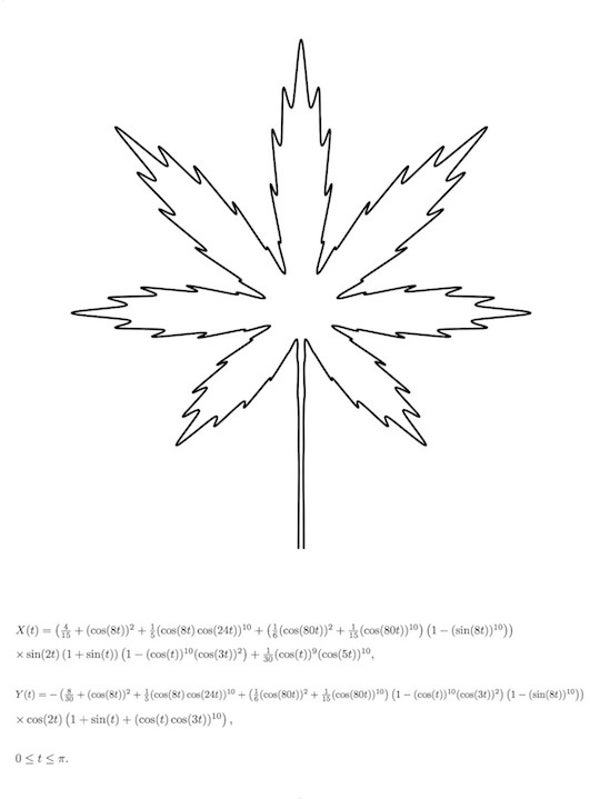
日本楓葉。致謝:Hamid Naderi Yeganeh。
橡樹葉
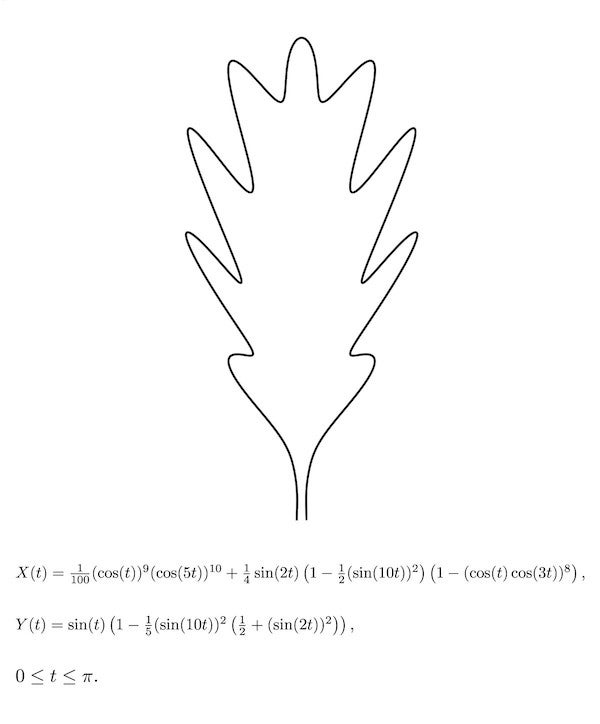
橡樹葉。致謝:Hamid Naderi Yeganeh
此外,在下面您可以看到透過繪製數千個圓圈建立的兩個數學圖形。圓圈的半徑和中心由三角函式確定。
橄欖枝
.jpg?w=600)
橄欖枝。致謝:Hamid Naderi Yeganeh
棕櫚枝

棕櫚枝。致謝:Hamid Naderi Yeganeh