關鍵概念
數學
幾何學
分形
尺度
介紹
你有沒有想過數學家研究什麼——以及為什麼?他們所做的大部分事情都複雜且難以理解,但分形藝術可能會讓我們一窺究竟。數學家研究分形,這些是自然產生的圖形,用於許多科學和技術領域。但你不必成為數學家也能欣賞它們的美麗。你知道你也可以創造一個嗎?在這個活動中,你將拿出一些顏料來創作藝術品——並發現分形有多麼常見。
背景
分形是幾何圖形。它們很難正式定義,但它們的特徵和美麗使它們易於理解且引人入勝。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來有關塑造我們當今世界的發現和想法的具有影響力的故事。
一個特徵是自相似性,它描述了分形如何在不同尺度上具有重複出現的模式。換句話說,當您放大時,您會發現最初看到的模式的較小版本。當您進一步放大時,您會發現該模式的更小版本,依此類推。這似乎會無限期地持續下去。
分形縮放的方式是另一個使其與傳統幾何圖形(如直線、正方形和立方體)區分開來的特徵。當您將線段的長度加倍時,原始線段將適合兩次(或 21)其中,使線成為一維的。如果您將正方形邊長加倍,則原始正方形將適合四次(或 22)在新、更大的正方形中,使正方形成為二維的。在立方體上執行相同的操作,原始立方體將適合八次(或 23)到新圖形中,使立方體成為三維的。在分形上應用此操作,原始分形適合較大分形的次數可能是三、五或任何其他不是 2 的整數次冪的數字。這是分形的特徵。它們具有分數維度,例如 8/5。
最後一個令人驚訝的事實:一些分形可以顯示無限的周長,即使它們的面積是有限的。這是您可以在即將創作的藝術品中探索的內容。
材料
舊報紙(用於保護您的工作區域)
舊 CD 盒
指畫顏料
紙巾或布
水
用於製作印花的紙張(手指畫紙效果最佳。)
放大鏡(可選)
準備
保護您的工作區。
拆卸 CD 盒,使您有兩個鬆動的蓋子。
將其中一個蓋子平放面朝上放在您的工作區上,蓋子的邊緣在其下方。
步驟
在蓋子中心新增一滴葡萄大小的顏料。
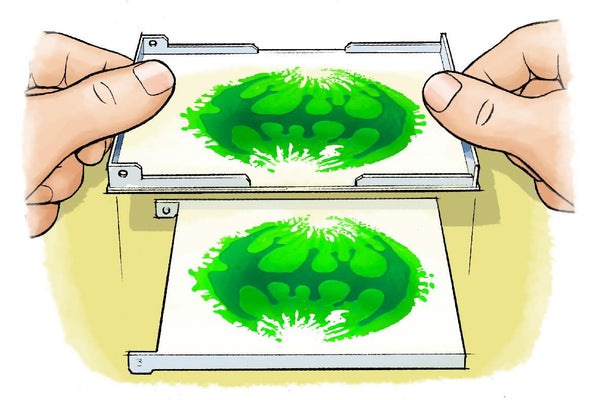
將第二個蓋子放在第一個蓋子頂部,平面朝下,使顏料擠壓在兩個蓋子的平面區域之間,並且蓋子的邊緣朝外。你注意到什麼了?顏料會擴散嗎?它形成什麼型別的幾何圖形?
檢視這個圖形的周長。它比 CD 盒的周長長還是短得多?
當您輕輕地將兩個蓋子壓在一起然後再次鬆開時會發生什麼?幾何圖形會改變嗎?會形成像懸崖或其他分支模式的圖案嗎?
您認為當您剝下頂蓋時會發生什麼?圖形會改變嗎?它會分支更多嗎?您會得到兩個圖形,每個蓋子上一個嗎?如果是這樣,它們會相同嗎?
將盒子放回工作區,小心地提起頂蓋。當您這樣做時,儘量不要將蓋子相互滑動,而是直接向上提起。
檢視結果圖形。您的預測正確嗎?
選擇一個圖形並找到一個圖案。然後,看看你是否能在你的圖形中找到這個圖案的更大或更小的版本。數學家將彼此的複製品——但其中一個可以比另一個更大或更小的圖形或圖案稱為“相似”圖形或圖案。
將您的蓋子平面朝下放在紙上以形成印花。您認為印刷的圖形會是 CD 盒上圖形的精確複製品嗎?為什麼是或為什麼不是?
剝下蓋子。再次,避免將蓋子在紙上滑動。您的預測正確嗎?您的印刷版本更詳細還是更少?
分形是幾何圖形,其圖案在多個放大級別上重複出現。您能在您的圖形中找到圖案的更小和更大的版本嗎?如果可以,您就創造了分形!
如果您有放大鏡,請使用它放大並檢視是否可以在更小的尺度上找到相同的圖案。在越來越小的尺度上重新出現的圖案是分形的典型特徵。
檢視您分形的周長。想象一下在您的圖形周圍放置細繩,匹配其邊緣的最小細節並切割細繩,使其剛好覆蓋您圖形的周長。然後想象一下拉伸這根細繩。它會比 CD 盒的周長長還是短得多?現在想象一下分形會分支成越來越小的細節。分形的周長會發生什麼?它的面積會增長得那麼快嗎?這個分形還能放在 CD 盒上還是需要更大的表面?
製作和研究更多印花。完成印刷後,清潔蓋子並透過新增新的顏料重複此過程。您的新圖形與第一個圖形有何相似之處,又有何不同?嘗試組合不同的顏色,探索什麼能產生最美麗的分形。
這些印花讓您想到什麼?它們像您知道的東西嗎?
額外內容:仔細觀察西蘭花冠或羅馬花椰菜。如果您在商店找不到,請在網際網路上查詢一些圖片。您能看到相同的圖案如何在不同尺寸下出現嗎?
額外內容:環顧四周。你能在自然界中找到分形嗎?看看樹木、樹葉、蕨類植物甚至雲彩。這些也是分形嗎?為什麼是或為什麼不是?
額外內容:一些分形由一個圖形組成,該圖形包含無限多個越來越小的自身版本。點選“更多探索”部分中列出的連結,瞭解謝爾賓斯基三角形。觀看影片,因為它會放大。您看到圖案如何在越來越小的尺度上無限重複自身嗎?你能畫一個謝爾賓斯基三角形嗎?你能自己製作一個這種型別的分形嗎?
額外內容:在網際網路上查詢一些計算機生成的分形和自然界中出現的分形的影像。有沒有一些你覺得特別令人印象深刻的?
觀察和結果
您是否在不同尺度上發現了重複出現的圖案?您是否看到了分支圖案的出現?
顏料喜歡粘在一起。當您首先將顏料擠壓在蓋子之間,然後釋放或拉開蓋子時,顏料內部以及顏料與塑膠蓋子之間的相互作用會產生令人印象深刻的分形。在光面紙上印刷可以讓您重複此過程並建立顯示更精細分支的圖案。
雖然您的圖形面積變化不大,但當新增越來越多的分支時,其周長增長很快。
分形在自然界中很常見。樹木、樹葉、蕨類植物、貝殼、閃電和雲彩只是一些例子。分形不僅在我們周圍,而且也在我們內部:我們的肺和血管顯示出分形特徵。分形數學可以幫助我們描述和量化這些結構。工程師也使用分形來創造新產品,例如手機天線。分形藝術是一種數字藝術形式,藝術家使用計算機生成的影像來建立複雜的物體。
清理
用肥皂水清洗所有裝置。
更多探索 什麼是分形?,來自分形基金會
地球上最令人驚歎的自然分形圖案,來自《連線》 謝爾賓斯基三角形,來自萊斯大學
此活動與科學夥伴合作推出