關鍵概念
數學
圖案
干涉
光學錯覺
介紹
你有沒有想過為什麼我們的眼睛會被圖案吸引? 我們在藝術和音樂中,以及在日常生活中都看到圖案。 圖案可以提供秩序感,並使看似忙亂的世界變得更容易管理。 它們是許多假設和預測的基礎。 如果我們總是這樣做,我們就會假設我們會在中午吃午飯。 我們預測雷雨雲會帶來雨水。 而且當你違反規則時,你可能會預料到會遇到麻煩。
我們太習慣於尋找圖案,以至於我們甚至可能會在沒有圖案的地方看到圖案。 在這項活動中,我們尋找其中一種錯覺:一種印刷商避免但科學家們已經很好地利用的錯覺。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和想法的具有影響力的故事的未來。
背景
有時整體大於部分之和。 這對於干涉圖案來說絕對是正確的,干涉圖案是波以建設性或破壞性方式相交的結果。 在聲學中,兩個頻率略有不同的波的干涉會產生拍頻,或音量的週期性變化。 在光學中,雙縫實驗表明,兩個略微位移的、頻率相同的光波的干涉會產生一系列明暗相間的條紋。 一種鮮為人知的干涉圖案——莫爾干涉圖案——發生在具有透明間隙的規則圖案與另一個類似圖案重疊時。 這兩個圖案必須幾乎完全重疊或幾乎相同。 為了使干涉圖案發生,小的位移、旋轉或週期差異等是必不可少的。
莫爾圖案是許多人的敵人:在印刷中,點的排列會產生不受歡迎的莫爾圖案;在電視和數碼攝影中,物體上的圖案會干擾光感測器或相機感測器的圖案,從而在圖片中新增不需要的莫爾圖案。 另一方面,科學家們已設法在用於進行微觀測量的工具中利用莫爾圖案的優勢。 莫爾圖案在那裡很有吸引力,因為所建立圖案的週期性放大了干涉圖案的微小差異。
材料
梳子(至少兩個應該相同,或者針腳在厚度和間距上幾乎相同。)
兩個螢幕,例如窗紗,其中至少一個可以自由操作
尼龍襪
與您的材料顏色形成對比的表面或背景,以幫助發現圖案
準備
將您的材料收集在您的工作空間中。
步驟
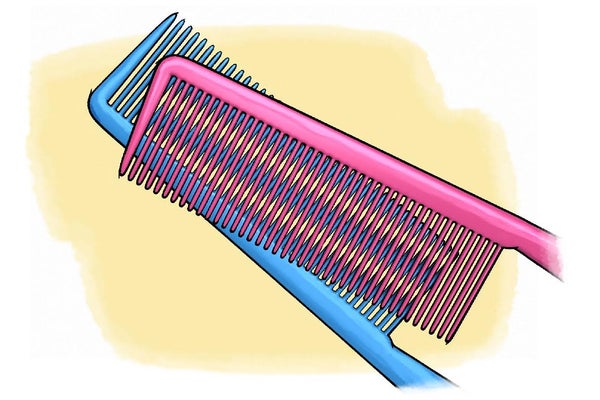
從一對梳子開始。 將它們分別放在對比鮮明的背景上。 您將如何描述針腳的圖案?它是規則的還是不規則的? 針腳間隔很遠還是彼此靠近?
如果您將兩個相同的梳子完全疊放在一起,使它們完美重疊,您期望您觀察到的針腳圖案會發生什麼變化? 如果您使兩個梳子幾乎完美對齊,會有什麼不同嗎?
測試您的預測。 如果您沒有兩個相同的梳子,請使用兩個針腳圖案非常相似的梳子。 你看到你預測的了嗎?
如果梳子稍微錯位,或者它們的針腳圖案略有不同,您應該會看到第三種圖案出現:一種重複部分之間的距離是梳子單個針腳之間距離的幾倍的圖案。 如果您看不到它,請嘗試不同的梳子組合或將頂部梳子與底部梳子交換。 擁有對比鮮明的背景也會有所幫助。
慢慢地左右移動頂部梳子。 你現在觀察到什麼?
將梳子相對於彼此旋轉一個小角度。 圖案會改變嗎? 如果您增加旋轉角度會發生什麼? (提示:注意出現的圖案的重複部分之間的距離。)
測試不同梳子的組合,以找出使這些圖案出現所必需的條件。
您剛剛探索了平行線的重疊圖案。 您認為如果您重疊其他圖案(例如正方形圖案),會發生同樣的事情嗎?
看看窗紗。 你看到正方形的圖案了嗎? 請注意,正方形的大小決定了這個圖案的重複部分之間的距離。
觀察第二個窗紗。 它有大小相似的正方形嗎?
思考片刻。 您將如何將兩個螢幕放在一起以建立第三種圖案? 想想這與您的梳子實驗有何相似之處和不同之處。
如果可以,請嘗試一下。 會出現新的圖案嗎?
當您更改螢幕之間的旋轉角度時,圖案會如何變化?
想象一下縮小窗紗中的正方形,直到它們變得很小。 它看起來幾乎像透過單層尼龍襪看東西嗎? 您認為可以透過重疊多層尼龍襪來建立圖案嗎?為什麼或者為什麼不?
進行測試。 在均勻、對比鮮明的背景下,透過兩層尼龍看。 您看到出現圖案了嗎? 它們與您之前看到的圖案有何相似和不同之處?
附加題: 您在這項活動中觀察到的是莫爾圖案。 您能在房子周圍找到其他莫爾圖案嗎,例如摺疊的薄窗簾,或者在外面開車或在城鎮周圍散步時? 注意鏈條圍欄。 圍欄及其陰影甚至可以結合起來形成莫爾圖案。 觀察圖案如何隨著您的移動而變化。
附加題: 使用計算機印表機在兩張透明膠片上列印相同的線條或同心圓圖案。 您可以透過相對於彼此移動或旋轉這些透明膠片來建立藝術性的莫爾圖案嗎?
附加題: 使用線上莫爾圖案生成器建立一些漂亮的圖案。 嘗試預測當您更改其中一個引數時,圖案將如何變化。
觀察和結果
當兩個相同(或幾乎相同)的重複圖案重疊時,您是否看到圖案出現? 當您增加旋轉角度時,重複部分之間的距離是否減小?
出現的圖案稱為莫爾圖案。 它們放大了兩個相同或幾乎相同的重複圖案之間的微小差異。 如果您有相同的梳子並且可以完全對齊它們,則不應看到莫爾圖案。 正是圖案的微小差異或微小的未對準導致了清晰可見的長程莫爾圖案。 您是否注意到未對準的增加——更大的位移、更大的旋轉角度或初始圖案的更大差異——使得莫爾圖案中重複部分之間的距離減小? 一旦兩個初始圖案的差異或未對準太大,您將無法再檢測到莫爾圖案。
莫爾圖案並非真實存在; 它們是在您眼睛的影像中產生的光學錯覺。
更多探索 光學錯覺:莫爾圖案生成器,來自分子表達
雙縫科學:光如何既是粒子又是波,來自大眾科學 日全食期間的陰影帶,來自Strickling.net
幽靈科學:製造鬼魅般的幻覺,來自大眾科學
此活動由科學夥伴合作推出